1.2.1 函数的概念 说课课件(人教A版必修1)
文档属性
| 名称 | 1.2.1 函数的概念 说课课件(人教A版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-17 00:00:00 | ||
图片预览








文档简介
(共36张PPT)
一、教材分析
1、教材的地位与作用
函数一章在高中数学的学习中起着承上启下的作用。
加深对函数概念的理解,能为学生进一步学习函数的性质等知识提供了良好的保证,也为学生今后进一步学习高等数学奠定了基础。
本章的学习对中学生数学学习起着决定性的作用。而且不仅是知识性方面,更重要的学习方法方面,也将是终身受益的一章。作为该章的起始课之一,本节课的教学非常的重要。
一、教材分析
2、教学目标及确立的依据
教学知识目标:
通过丰富实例,使学生建立起函数的概念背景,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;
了解构成函数的三个要素;
理解函数的抽象符号。
一、教材分析
2、教学目标及确立的依据
能力训练目标:
通过教学培养学生的抽象概括能力和逻辑思维能力,培养学生理论联系实际的能力。
德育渗透目标:
培养学生坚韧不拔的意志,实事求是的科学态度,使学生懂得一切事物都是在不断变化、相互联系和相互制约的辩正唯物主义观点。
一、教材分析
3、教学重点难点及确立的依据
教学重点:
在集合与对应的基础上理解函数的概念,体会函数是描述变量之间的依赖关系的重要数学模型。
教学难点:
函数概念及函数符号y=f(x)的理解。
二、教法学法
1、教法分析
启发探究法为主
讨论法、练习法为辅
二、教法学法
2、学法分析
自主学习
协作学习
合作探究
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
1、创设情景,导入课题
(1)回顾初中所学的函数;
(2)回顾初中的函数定义;
(3)展示三个问题情景。
情景1:炮打活人
27日下午,美国奇人
戴维史密斯当着600多名观
众的面,充当了“人体炮
弹”。他被成功“打”到约50米的高度,然后轻松越
过6米高的边界护栏,经过20秒后,史密斯最终安全
无恙地落入助手设在美国境内的保护网里。史密斯距
地面的高度h(单位:m)随时间t(单位:s)变化的规律
是:
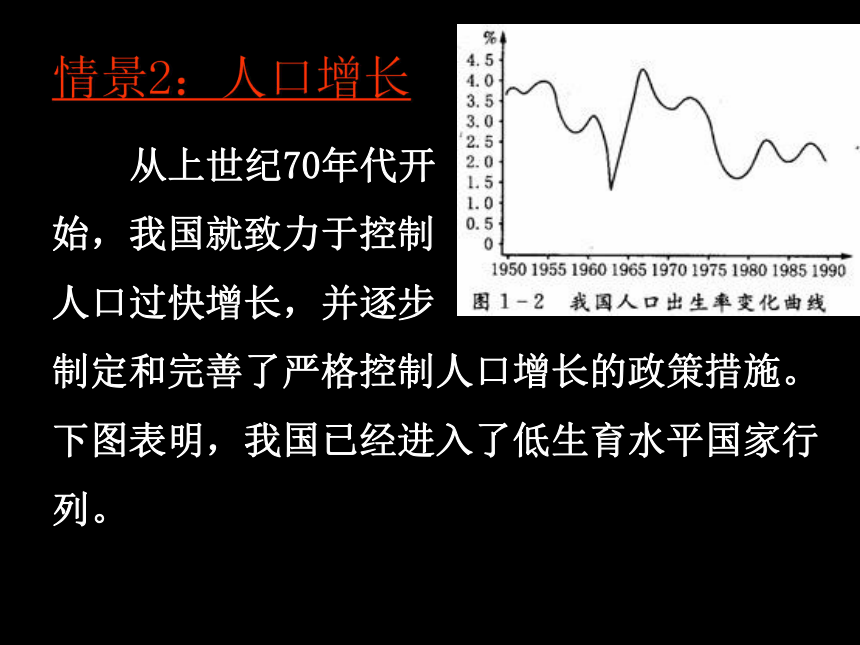
情景2:人口增长
从上世纪70年代开
始,我国就致力于控制
人口过快增长,并逐步
制定和完善了严格控制人口增长的政策措施。
下图表明,我国已经进入了低生育水平国家行
列。
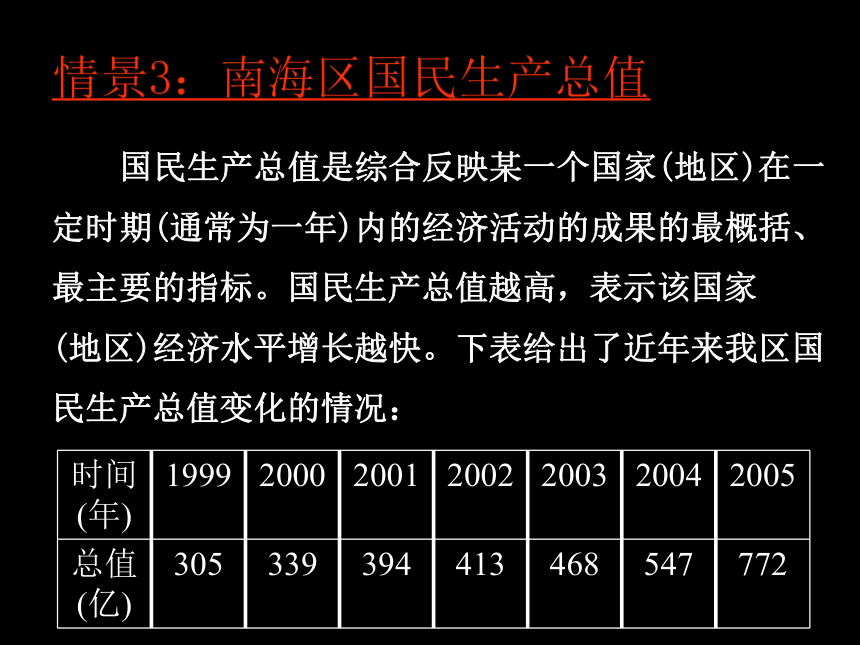
情景3:南海区国民生产总值
国民生产总值是综合反映某一个国家(地区)在一
定时期(通常为一年)内的经济活动的成果的最概括、
最主要的指标。国民生产总值越高,表示该国家
(地区)经济水平增长越快。下表给出了近年来我区国
民生产总值变化的情况:
时间(年) 1999 2000 2001 2002 2003 2004 2005
总值(亿) 305 339 394 413 468 547 772
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
2、自主探究,合作交流
【解决重点,突破难点】
引导学生分析、归纳三个实例的共同点
区分初中和高中的函数概念
用新观点分析初中熟悉的三个函数
【探究活动一】
将学生分成若干小组,让学生分析、归纳三个实
例的共同特点是什么。
(1)引导学生分析三个实例的共同点
(1)出现了两个集合A和B;
(2)当集合A中的元素x确定下来以后,
在集合B中都能找到惟一的元素y与之对
应。
【函数的概念】
设A,B是非空数集,如果按照某种确定的对应
关系f,使对于集合A中的任意一个数,在集合B中
都有惟一确定的数f(x)和它对应,那么就称f:A→B
为从集合A到集合B的一个函数,记作y=f(x),x∈A。
其中,x叫做自变量,x的取值范围A叫做函数的定
义域;与x的值相对应的y值叫做函数值,函数值的
集合{f(x)|x∈A}叫做函数的值域。
【探究活动二】
判断下列实例中的变量是否
是函数关系:
(1)坐电梯时,电梯距离地
面的高度h与时间t之间的关系;
(2)广州地铁票价和站数之
间的关系。
(2)区别初中和高中的函数定义
函数的本质:x定y定。
【探究活动三】
请同学们用集合与对应的观点分析初中所学的
一次函数,二次函数和反比例函数,并说出它们的
定义域和值域。
(3)用新观点分析初中所学的三个函数
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
3、巩固练习,深化知识
【解决重点,突破难点】
理解函数符号y=f(x)是本节课的另一个难点,我首先通过例题的讲解进行示范,然后设置相应的练习题,通过师生之间的共同讨论来帮助学生深刻理解函数符号。
【例1】
若 ,则 , 的值
是多少?
【例2】
已知函数 。
(1)求函数的定义域;
(2)求 、 的值;
(3)当 时,求 和 的值。
【练习1】
由下列式子是否能确定y是x的函数?
【练习2】
下列图象能否表示函数y=f(x)的图象。
【练习3】
若 ,求 , ,
, 的值。
【练习4】
求下列函数的定义域:
【练习5】
已知函数 ,
那么 的值是多少?
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
4、归纳小结,反思提高
【小结以问题的形式出现】
问题:通过本节课的学习,你认为函数的概念是什么?要学好函数的概念,你觉得需要注意什么问题?
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
5、布置作业,分层落实
求下列函数的定义域:
【必做题1】
【必做题2】
若 ,求 ,
, , 的值。
【必做题3】
已知函数 。
(1)点(3,14)在 的图象上吗;
(2)当 时,求 的值;
(3)当 时,求 的值。
【选做题4】
阅读课本第29页的阅读材料——《函数概
念的发展历程》,综合本节课所学的内容,写
一篇与函数概念发展史有关的数学小论文。
因为函数的概念非常的抽象,因此
函数概念的学习一直是历届学生学习的
难点,函数概念的教学也一直是教师教
学的难点。借这一次难得的说课机会,
我向各位专家评委汇报了我对这节课的
教学设计,恳请各位专家评委提出宝贵
的意见,谢谢。
一、教材分析
1、教材的地位与作用
函数一章在高中数学的学习中起着承上启下的作用。
加深对函数概念的理解,能为学生进一步学习函数的性质等知识提供了良好的保证,也为学生今后进一步学习高等数学奠定了基础。
本章的学习对中学生数学学习起着决定性的作用。而且不仅是知识性方面,更重要的学习方法方面,也将是终身受益的一章。作为该章的起始课之一,本节课的教学非常的重要。
一、教材分析
2、教学目标及确立的依据
教学知识目标:
通过丰富实例,使学生建立起函数的概念背景,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;
了解构成函数的三个要素;
理解函数的抽象符号。
一、教材分析
2、教学目标及确立的依据
能力训练目标:
通过教学培养学生的抽象概括能力和逻辑思维能力,培养学生理论联系实际的能力。
德育渗透目标:
培养学生坚韧不拔的意志,实事求是的科学态度,使学生懂得一切事物都是在不断变化、相互联系和相互制约的辩正唯物主义观点。
一、教材分析
3、教学重点难点及确立的依据
教学重点:
在集合与对应的基础上理解函数的概念,体会函数是描述变量之间的依赖关系的重要数学模型。
教学难点:
函数概念及函数符号y=f(x)的理解。
二、教法学法
1、教法分析
启发探究法为主
讨论法、练习法为辅
二、教法学法
2、学法分析
自主学习
协作学习
合作探究
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
1、创设情景,导入课题
(1)回顾初中所学的函数;
(2)回顾初中的函数定义;
(3)展示三个问题情景。
情景1:炮打活人
27日下午,美国奇人
戴维史密斯当着600多名观
众的面,充当了“人体炮
弹”。他被成功“打”到约50米的高度,然后轻松越
过6米高的边界护栏,经过20秒后,史密斯最终安全
无恙地落入助手设在美国境内的保护网里。史密斯距
地面的高度h(单位:m)随时间t(单位:s)变化的规律
是:
情景2:人口增长
从上世纪70年代开
始,我国就致力于控制
人口过快增长,并逐步
制定和完善了严格控制人口增长的政策措施。
下图表明,我国已经进入了低生育水平国家行
列。
情景3:南海区国民生产总值
国民生产总值是综合反映某一个国家(地区)在一
定时期(通常为一年)内的经济活动的成果的最概括、
最主要的指标。国民生产总值越高,表示该国家
(地区)经济水平增长越快。下表给出了近年来我区国
民生产总值变化的情况:
时间(年) 1999 2000 2001 2002 2003 2004 2005
总值(亿) 305 339 394 413 468 547 772
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
2、自主探究,合作交流
【解决重点,突破难点】
引导学生分析、归纳三个实例的共同点
区分初中和高中的函数概念
用新观点分析初中熟悉的三个函数
【探究活动一】
将学生分成若干小组,让学生分析、归纳三个实
例的共同特点是什么。
(1)引导学生分析三个实例的共同点
(1)出现了两个集合A和B;
(2)当集合A中的元素x确定下来以后,
在集合B中都能找到惟一的元素y与之对
应。
【函数的概念】
设A,B是非空数集,如果按照某种确定的对应
关系f,使对于集合A中的任意一个数,在集合B中
都有惟一确定的数f(x)和它对应,那么就称f:A→B
为从集合A到集合B的一个函数,记作y=f(x),x∈A。
其中,x叫做自变量,x的取值范围A叫做函数的定
义域;与x的值相对应的y值叫做函数值,函数值的
集合{f(x)|x∈A}叫做函数的值域。
【探究活动二】
判断下列实例中的变量是否
是函数关系:
(1)坐电梯时,电梯距离地
面的高度h与时间t之间的关系;
(2)广州地铁票价和站数之
间的关系。
(2)区别初中和高中的函数定义
函数的本质:x定y定。
【探究活动三】
请同学们用集合与对应的观点分析初中所学的
一次函数,二次函数和反比例函数,并说出它们的
定义域和值域。
(3)用新观点分析初中所学的三个函数
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
3、巩固练习,深化知识
【解决重点,突破难点】
理解函数符号y=f(x)是本节课的另一个难点,我首先通过例题的讲解进行示范,然后设置相应的练习题,通过师生之间的共同讨论来帮助学生深刻理解函数符号。
【例1】
若 ,则 , 的值
是多少?
【例2】
已知函数 。
(1)求函数的定义域;
(2)求 、 的值;
(3)当 时,求 和 的值。
【练习1】
由下列式子是否能确定y是x的函数?
【练习2】
下列图象能否表示函数y=f(x)的图象。
【练习3】
若 ,求 , ,
, 的值。
【练习4】
求下列函数的定义域:
【练习5】
已知函数 ,
那么 的值是多少?
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
4、归纳小结,反思提高
【小结以问题的形式出现】
问题:通过本节课的学习,你认为函数的概念是什么?要学好函数的概念,你觉得需要注意什么问题?
三、教学过程
自主探究,合作交流
巩固练习,深化知识
归纳小结,反思提高
创设情景,导入课题
布置作业,分层落实
5、布置作业,分层落实
求下列函数的定义域:
【必做题1】
【必做题2】
若 ,求 ,
, , 的值。
【必做题3】
已知函数 。
(1)点(3,14)在 的图象上吗;
(2)当 时,求 的值;
(3)当 时,求 的值。
【选做题4】
阅读课本第29页的阅读材料——《函数概
念的发展历程》,综合本节课所学的内容,写
一篇与函数概念发展史有关的数学小论文。
因为函数的概念非常的抽象,因此
函数概念的学习一直是历届学生学习的
难点,函数概念的教学也一直是教师教
学的难点。借这一次难得的说课机会,
我向各位专家评委汇报了我对这节课的
教学设计,恳请各位专家评委提出宝贵
的意见,谢谢。
