1.2.2 函数的表示法 第一课时 课件(人教A版必修1)
文档属性
| 名称 | 1.2.2 函数的表示法 第一课时 课件(人教A版必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-17 04:23:15 | ||
图片预览








文档简介
(共35张PPT)
1.2.2 函数的表示法(一)
1.掌握函数的三种表示方法:列表法、图象法、解析法,体会三种表示方法的特点.
2.掌握函数图象的画法及解析式的求法.
表示函数的方法常用的有:
(1)解析法——用 表示两个变量之间的对应关系;
(2)图象法——用 表示两个变量之间的对应关系;
(3)列表法——列出 来表示两个变量之间的对应关系.
自学导引
数学表达式
图象
表格
任何一个函数都可以用解析法表示吗?
答:不一定.如某一地区绿化面积与年份关系等受偶然因素影响较大的函数关系等无法用解析式表示.
自主探究
1.已知函数f(x)由下表给出,则f(3)的值为( )
A.-1 B.-2 C.-3 D.-4
解析:由表可知f(3)=-4,故选D.
答案:D
预习测评
x 1 2 3 4
f(x) -3 -2 -4 -1
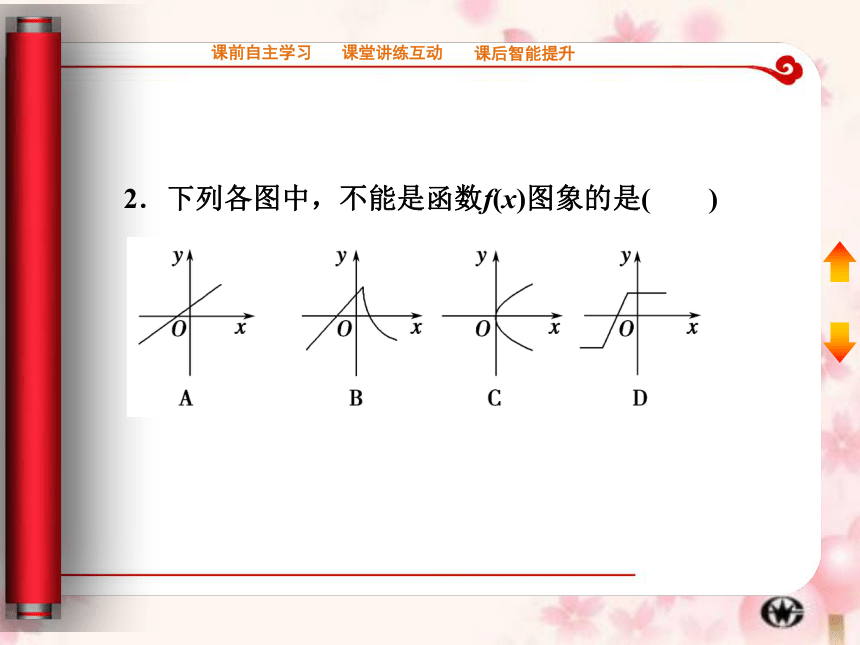
2.下列各图中,不能是函数f(x)图象的是( )
解析:结合函数的定义知,对A、B、D,定义域中每一个x都有唯一函数值与之对应,而对C,对大于0的x而言,有两个不同值与之对应,不符合函数定义,故选C.
答案:C
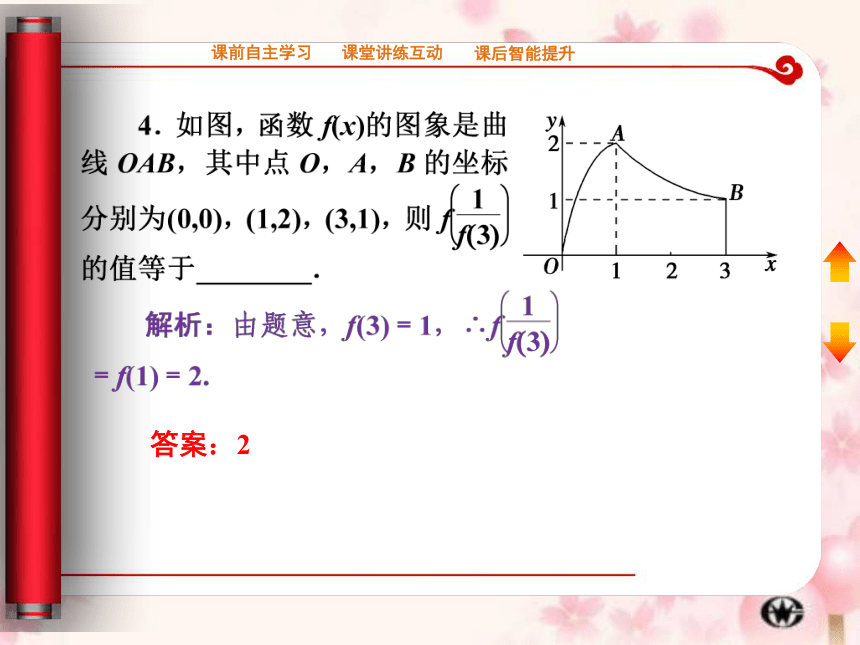
答案:2
函数的三种表示方法的优缺点比较
要点阐释
优 点 缺 点
解析法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式表示出来
优 点 缺 点
列表法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取较少的有限值的对应关系
图象法 能形象直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
题型一 函数的表示法
典例剖析
(1)写出函数t的解析式;
(2)用列表法表示此函数;
(3)画出函数t的图象.
解:(1)由题设条件知:当x=2时,t=100,
所以函数的定义域是{x|0(2)x=1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16, 17,18,19,20,共取20个值,列表如下:
x 1 2 3 4 5 6 7 8 9 10
t 197 100 68.3 53 44.2 38.7 35 32.5 30.8 29.6
11 12 13 14 15 16 17 18 19 20
28.8 28.3 28.1 28 28.1 28.25 28.5 28.9 29.3 29.8
注:表中的部分数据是近似值.
(3)函数t的图象是由20个点组成的一个点列.如图所示.
点评:在实际研究一个函数时,通常是将上述三种表示法结合起来使用,即解析式→列表→描点,画出图象,然后再总结出函数的性质.三种方法相互兼容和补充,各有优缺点,在实际操作中,仍以解析法为主.
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
试用另外两种表示方法表示函数M=f(m).
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
信函质量
(m/g) 0邮资
M/元 1.2 2.4 3.6 4.8 6.0
解:已知给出的是用列表法表示的函数M=f(m),该函数是分段函数.
由解析式可得到分段函数的简图,从而得到表示函数M=f(m)的另一种方法,即图象法.
题型二 作函数的图象
【例2】 作出下列函数图象:
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3).
解:(1)因为x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2}.
所以图象为一直线上的孤立点(如图(1)).
(2)∵y=2(x-1)2-5,∴当x=0时,y=-3;
当x=3时,y=3;当x=1时,y=-5.
所画函数图象如图(2).
点评:一般地,作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式(可能有的要表示为分段函数),再列表描出图象,并在画图象的同时注意一些关键点,如与坐标轴的交点、分段函数的区间端点等.
解:(1)当x=1时,y=1,所画函数图象如图1
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
(2)y=x2-4x+3=(x-2)2-1,
且x=1,3时,y=0;当x=2时,y=-1.所画函数图象如图2.
题型三 求函数解析式
【例3】 求下列函数的解析式:
(1)已知f(x)为一次函数,且f[f(x)]=4x-1,求f(x);
解:(1)(待定系数法)因为f(x)是一次函数.
设f(x)=kx+b(k≠0).
解法二:(配凑法)
点评:求函数解析式的常用方法是待定系数法和换元法.当已知函数的类型时,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.
当不知函数类型时,一般可采用换元法,所谓换元法即将接受对象“+1”换作另一个字母“t”,然后从中解出x与t的关系,代入原式中便可求出关于“t”的函数关系,此即为所求函数解析式,但要注意自变量取值范围的变化情况.
另外,求函数解析式的方法还有配凑法、解方程组法等.
3.已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
解:设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
又∵f(x+1)-f(x)=2x,对任意x∈R成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
【例4】 已知f(x2+2)=x4+4x2,求f(x)的解析式.
错解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4,∴f(x)=x2-4.
错因分析:本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
误区解密 因忽略函数的定义域而出错
正解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
纠错心得:采用换元法求函数的解析式时,一定要注意换元后的自变量的取值范围.如本题中令t=x2+2后,则t≥2.
1.函数的三种表示方法:解析法、列表法、图象法.
2.画函数图象的方法:(1)列表、描点、连线;(2)图象变换.
3.求函数解析式的方法有:换元法、配凑法、待定系数法等.
课堂总结
1.2.2 函数的表示法(一)
1.掌握函数的三种表示方法:列表法、图象法、解析法,体会三种表示方法的特点.
2.掌握函数图象的画法及解析式的求法.
表示函数的方法常用的有:
(1)解析法——用 表示两个变量之间的对应关系;
(2)图象法——用 表示两个变量之间的对应关系;
(3)列表法——列出 来表示两个变量之间的对应关系.
自学导引
数学表达式
图象
表格
任何一个函数都可以用解析法表示吗?
答:不一定.如某一地区绿化面积与年份关系等受偶然因素影响较大的函数关系等无法用解析式表示.
自主探究
1.已知函数f(x)由下表给出,则f(3)的值为( )
A.-1 B.-2 C.-3 D.-4
解析:由表可知f(3)=-4,故选D.
答案:D
预习测评
x 1 2 3 4
f(x) -3 -2 -4 -1
2.下列各图中,不能是函数f(x)图象的是( )
解析:结合函数的定义知,对A、B、D,定义域中每一个x都有唯一函数值与之对应,而对C,对大于0的x而言,有两个不同值与之对应,不符合函数定义,故选C.
答案:C
答案:2
函数的三种表示方法的优缺点比较
要点阐释
优 点 缺 点
解析法 一是简明、全面地概括了变量间的关系;二是通过解析式可以求出任意一个自变量所对应的函数值 不够形象、直观、具体,而且并不是所有的函数都能用解析式表示出来
优 点 缺 点
列表法 不需要计算就可以直接看出与自变量的值相对应的函数值 它只能表示自变量取较少的有限值的对应关系
图象法 能形象直观地表示出函数的变化情况 只能近似地求出自变量的值所对应的函数值,而且有时误差较大
题型一 函数的表示法
典例剖析
(1)写出函数t的解析式;
(2)用列表法表示此函数;
(3)画出函数t的图象.
解:(1)由题设条件知:当x=2时,t=100,
所以函数的定义域是{x|0
x 1 2 3 4 5 6 7 8 9 10
t 197 100 68.3 53 44.2 38.7 35 32.5 30.8 29.6
11 12 13 14 15 16 17 18 19 20
28.8 28.3 28.1 28 28.1 28.25 28.5 28.9 29.3 29.8
注:表中的部分数据是近似值.
(3)函数t的图象是由20个点组成的一个点列.如图所示.
点评:在实际研究一个函数时,通常是将上述三种表示法结合起来使用,即解析式→列表→描点,画出图象,然后再总结出函数的性质.三种方法相互兼容和补充,各有优缺点,在实际操作中,仍以解析法为主.
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
试用另外两种表示方法表示函数M=f(m).
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
信函质量
(m/g) 0
M/元 1.2 2.4 3.6 4.8 6.0
解:已知给出的是用列表法表示的函数M=f(m),该函数是分段函数.
由解析式可得到分段函数的简图,从而得到表示函数M=f(m)的另一种方法,即图象法.
题型二 作函数的图象
【例2】 作出下列函数图象:
(1)y=1-x(x∈Z且|x|≤2);
(2)y=2x2-4x-3(0≤x<3).
解:(1)因为x∈Z且|x|≤2,
∴x∈{-2,-1,0,1,2}.
所以图象为一直线上的孤立点(如图(1)).
(2)∵y=2(x-1)2-5,∴当x=0时,y=-3;
当x=3时,y=3;当x=1时,y=-5.
所画函数图象如图(2).
点评:一般地,作函数图象主要有三步:列表、描点、连线.作图象时一般应先确定函数的定义域,再在定义域内化简函数解析式(可能有的要表示为分段函数),再列表描出图象,并在画图象的同时注意一些关键点,如与坐标轴的交点、分段函数的区间端点等.
解:(1)当x=1时,y=1,所画函数图象如图1
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
(2)y=x2-4x+3=(x-2)2-1,
且x=1,3时,y=0;当x=2时,y=-1.所画函数图象如图2.
题型三 求函数解析式
【例3】 求下列函数的解析式:
(1)已知f(x)为一次函数,且f[f(x)]=4x-1,求f(x);
解:(1)(待定系数法)因为f(x)是一次函数.
设f(x)=kx+b(k≠0).
解法二:(配凑法)
点评:求函数解析式的常用方法是待定系数法和换元法.当已知函数的类型时,可设出其函数解析式,利用待定系数法求解,这里包含着方程思想的应用.
当不知函数类型时,一般可采用换元法,所谓换元法即将接受对象“+1”换作另一个字母“t”,然后从中解出x与t的关系,代入原式中便可求出关于“t”的函数关系,此即为所求函数解析式,但要注意自变量取值范围的变化情况.
另外,求函数解析式的方法还有配凑法、解方程组法等.
3.已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.
解:设所求的二次函数为f(x)=ax2+bx+c(a≠0).
∵f(0)=1,∴c=1,则f(x)=ax2+bx+1.
又∵f(x+1)-f(x)=2x,对任意x∈R成立,
∴a(x+1)2+b(x+1)+1-(ax2+bx+1)=2x.
1.国内跨省市之间邮寄信函,每封信函的质量和对应邮资如下表:
【例4】 已知f(x2+2)=x4+4x2,求f(x)的解析式.
错解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
设t=x2+2,则f(t)=t2-4,∴f(x)=x2-4.
错因分析:本题错解的原因是忽略了函数f(x)的定义域.上面的解法,似乎是无懈可击,然而从其结论,即f(x)=x2-4来看,并未注明f(x)的定义域,那么按一般理解,就应认为其定义域是全体实数.但是f(x)=x2-4的定义域不是全体实数.
误区解密 因忽略函数的定义域而出错
正解:∵f(x2+2)=x4+4x2=(x2+2)2-4,
令t=x2+2(t≥2),则f(t)=t2-4(t≥2),
∴f(x)=x2-4(x≥2).
纠错心得:采用换元法求函数的解析式时,一定要注意换元后的自变量的取值范围.如本题中令t=x2+2后,则t≥2.
1.函数的三种表示方法:解析法、列表法、图象法.
2.画函数图象的方法:(1)列表、描点、连线;(2)图象变换.
3.求函数解析式的方法有:换元法、配凑法、待定系数法等.
课堂总结
