1.3.1 单调性与最大(小)值第一课时 课件(人教A版必修1)
文档属性
| 名称 | 1.3.1 单调性与最大(小)值第一课时 课件(人教A版必修1) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-17 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
1.3.1 单调性与最大(小)值
1.3 函数的基本性质
第1课时 函数的单调性
1.理解单调性的定义.
2.运用单调性的定义判断函数的单调性.
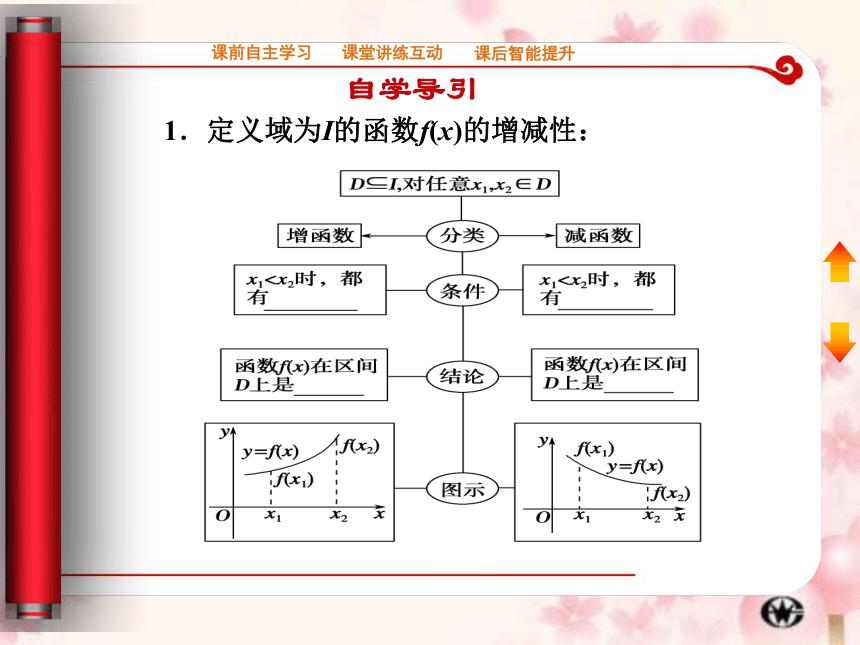
1.定义域为I的函数f(x)的增减性:
自学导引
2.如果函数y=f(x)在区间D上是_______或_______ ,那么就说函数y=f(x)在这一区间具有______________ ,区间D叫做y=f(x)的________ .
3.判断(证明)函数的单调性
判断(证明)函数单调性的步骤
自主探究
增函数
减函数
(严格的)单调性
单调区间
1.在增、减函数定义中,能否把“任意”两字去掉?
答:不能.如图所示
虽然f(-1)自主探究
2.如果函数在两个区间上都是单调的,在这两个区间的并集上是不是一定单调呢?
1.函数y=-x2的单调减区间是 ( )
A.[0,+∞) B.(-∞,0]
C.(-∞,0) D.(-∞,+∞)
解析:画出y=-x2在R上的图象,可知函数在[0,+∞)上递减.
答案:A
预习测评
A.函数f(x)先增后减
B.函数f(x)先减后增
C.函数f(x)是R上的增函数
D.函数f(x)是R上的减函数
答案:C
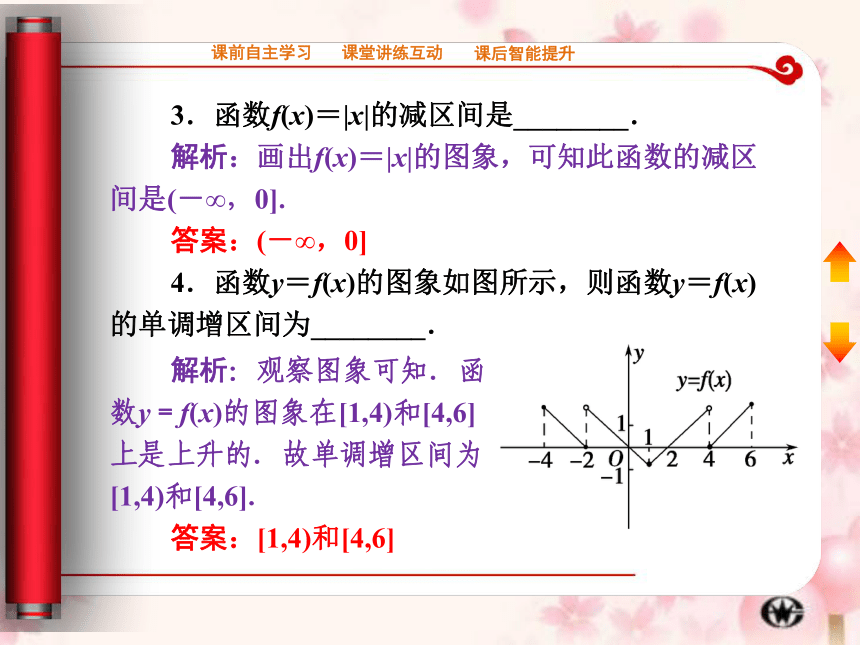
3.函数f(x)=|x|的减区间是________.
解析:画出f(x)=|x|的图象,可知此函数的减区间是(-∞,0].
答案:(-∞,0]
4.函数y=f(x)的图象如图所示,则函数y=f(x)的单调增区间为________.
解析:观察图象可知.函数y=f(x)的图象在[1,4)和[4,6]上是上升的.故单调增区间为[1,4)和[4,6].
答案:[1,4)和[4,6]
一、函数单调性的理解
1.如果一个函数在某个区间上是增函数或减函数,就说这个函数在这个区间上具有单调性,证明函数的单调性,必须严格按照单调性的定义证明.
2.定义中的x1、x2有三个特征:(1)“任意”性,不能由两个特殊值代替;(2)二者有大小,通常规定x13.函数的单调性是函数在某个区间上的性质.
(1)这个区间可以是整个定义域.如y=x在整个定义域(-∞,+∞)是增函数.
要点阐释
(2)这个区间也可以是定义域的真子集,如y=x2在定义域(-∞,+∞)不具备单调性,但在(-∞,0]是减函数,在[0,+∞)是增函数.
4.区间端点的写法
对于单独的一点,由于它的函数值是唯一确定的常数,没有增减变化,所以不存在单调问题.因此写单调区间时,如果端点在定义域内,可以包括端点,也可以不包括端点,但对于某些点无意义时,单调区间就不包括这些点.
5.求函数的单调区间,就是求函数保持同一单调性不变的最大区间.
二、函数单调性的判断与证明
1.函数单调性的判断方法有三种:一是依据单调性的定义;二是依据函数的图象;三是依据已知函数的单调性判断.如已学过的一次函数、二次函数、反比例函数的单调性情况.
2.函数单调性的证明方法:
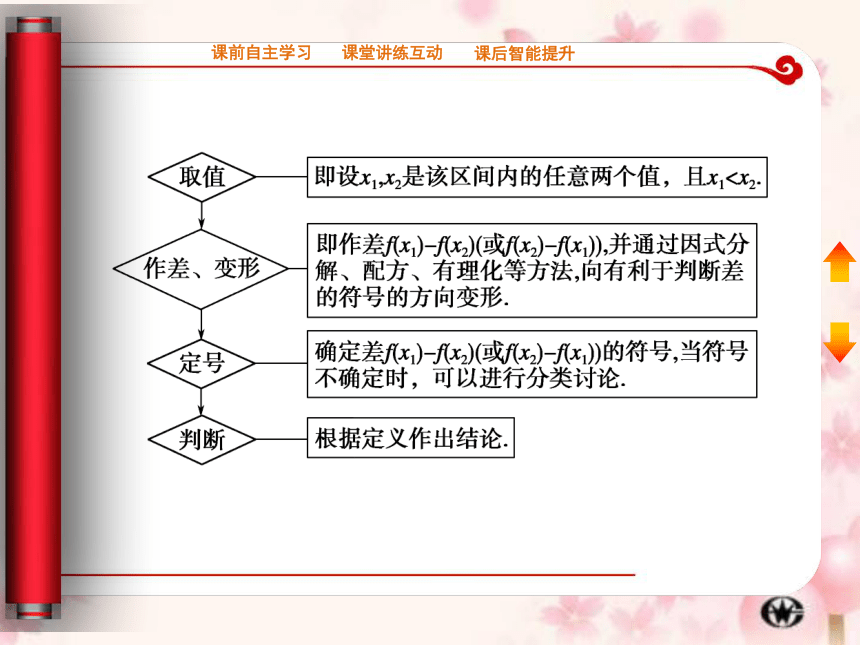
依据定义进行证明.其步骤如下:
①取值:即设x1,x2是该区间上的任意两个值,且x1②作差变形:即作差f(x1)-f(x2),并通过因式分解、配方、有理化等方法,向有利于判断差的符号的方向变形;
③定号:确定差f(x1)-f(x2)的符号,当符号不确定时,可以分情况讨论;
④判定:依据定义得出结论.
题型一 利用图象求函数的单调区间
【例1】 求下列函数的单调区间.
(1)f(x)=3|x|;
(2)f(x)=|x2+2x-3|.
典例剖析
f(x)在(-∞,0]上是减函数,在(0,+∞)上是增函数.
(2)令f(x)=x2+2x-3=(x+1)2-4.
先作出f(x)的图象,保留其在x轴及x轴上方部分,把它在x轴下方的图象翻到x轴上方就得到y=|x2+2x-3|的图象,如图所示.
由图象易得:函数的递增区间是(-3,-1),(1,+∞);
函数的递减区间是(-∞,-3],(-1,1].
点评:函数的单调区间可以是开的,也可以是闭的,也可以是半开半闭的,对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也单调.因此,只要单调区间端点使f(x)有意义,都可以使单调区间包括端点.但要注意,不连续的单调区间必须分开写,不能用“∪”符号连接它们.
1.求下列函数的单调区间
(2)f(x)=-x2+2|x|+3.
∴单调递增区间为(0,+∞),递减区间为(-∞,0).
(2)∵f(x)=-x2+2|x|+3
图象如图所示.
∴函数y=-x2+2|x|+3的单调递增区间为(-∞,-1],(0,1],递减区间为(-1,0],(1,+∞).
题型二 利用定义判定及证明函数单调性
点评:证明函数的单调性的常用方法是利用函数单调性的定义.其步骤为:(1)取值(注意x1、x2的任意性);(2)作差变形(目的是便于判断符号);(3)判断差的符号;(4)写出结论.
题型三 由函数的单调性求参数的取值范围
【例3】 已知函数f(x)=x2-2ax-3在区间[1,2]上单调,求实数a的取值范围.
解:函数f(x)=x2-2ax-3的图象开口向上,对称轴为直线x=a,画出草图如图所示.
由图象可知函数在(-∞,a]和(a,+∞)上分别单调,因此要使函数f(x)在区间[1,2]上单调,只需a≤1或a≥2(其中当a≤1时,函数f(x)在区间
[1,2]上单调递增;当a≥2时,函数f(x)在区间[1,2]上单调递减),从而a∈(-∞,1]∪ [2,+∞).
点评:已知函数的单调性求参数的取值范围,要注意数形结合思想,采用逆向思维.
3.已知函数f(x)=x2+2(a-1)x+2在区间 (-∞,4]上是减函数,求实数a的取值范围.
解:f(x)=x2+2(a-1)x+2
=[x+(a-1)]2-(a-1)2+2,
∴此二次函数的对称轴为x=1-a.
∴f(x)的单调减区间为(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.
误区解密 因对“单调区间”和“区间上单调”
两个概念混淆而出错
【例4】 若函数f(x)=x2+2(a-1)x+2的单调递减区间是(-∞,4],则实数a的取值范围是______.
错解:函数f(x)的图象的对称轴为直线x=1-a,由于函数在区间(-∞,4]上单调递减,因此1-a≥4,即a≤-3.
错因分析:错解中把单调区间误认为是在区间上单调.
正解:因为函数的单调递减区间为(-∞,4],且函数图象的对称轴为直线x=1-a,所以有1-a=4,即a=-3.
答案:a=-3
纠错心得:单调区间是一个整体概念,比如说函数的单调递减区间是I,指的是函数递减的最大范围为区间I.而函数在某一区间上单调,则指此区间是相应单调区间的子集.所以我们在解决函数的单调性问题时,一定要仔细读题,明确条件含义.
1.函数的单调区间必须是定义域的子集.因此讨论函数的单调性时,必须先确定函数的定义域.
课堂总结
3.求单调区间的方法:(1)图象法;(2)定义法;(3)利用已知函数的单调性.
4.用单调性的定义证明函数的单调性分四个主要步骤:
即“取值——作差变形——定号——判断”这四个步骤.
1.3.1 单调性与最大(小)值
1.3 函数的基本性质
第1课时 函数的单调性
1.理解单调性的定义.
2.运用单调性的定义判断函数的单调性.
1.定义域为I的函数f(x)的增减性:
自学导引
2.如果函数y=f(x)在区间D上是_______或_______ ,那么就说函数y=f(x)在这一区间具有______________ ,区间D叫做y=f(x)的________ .
3.判断(证明)函数的单调性
判断(证明)函数单调性的步骤
自主探究
增函数
减函数
(严格的)单调性
单调区间
1.在增、减函数定义中,能否把“任意”两字去掉?
答:不能.如图所示
虽然f(-1)
2.如果函数在两个区间上都是单调的,在这两个区间的并集上是不是一定单调呢?
1.函数y=-x2的单调减区间是 ( )
A.[0,+∞) B.(-∞,0]
C.(-∞,0) D.(-∞,+∞)
解析:画出y=-x2在R上的图象,可知函数在[0,+∞)上递减.
答案:A
预习测评
A.函数f(x)先增后减
B.函数f(x)先减后增
C.函数f(x)是R上的增函数
D.函数f(x)是R上的减函数
答案:C
3.函数f(x)=|x|的减区间是________.
解析:画出f(x)=|x|的图象,可知此函数的减区间是(-∞,0].
答案:(-∞,0]
4.函数y=f(x)的图象如图所示,则函数y=f(x)的单调增区间为________.
解析:观察图象可知.函数y=f(x)的图象在[1,4)和[4,6]上是上升的.故单调增区间为[1,4)和[4,6].
答案:[1,4)和[4,6]
一、函数单调性的理解
1.如果一个函数在某个区间上是增函数或减函数,就说这个函数在这个区间上具有单调性,证明函数的单调性,必须严格按照单调性的定义证明.
2.定义中的x1、x2有三个特征:(1)“任意”性,不能由两个特殊值代替;(2)二者有大小,通常规定x1
(1)这个区间可以是整个定义域.如y=x在整个定义域(-∞,+∞)是增函数.
要点阐释
(2)这个区间也可以是定义域的真子集,如y=x2在定义域(-∞,+∞)不具备单调性,但在(-∞,0]是减函数,在[0,+∞)是增函数.
4.区间端点的写法
对于单独的一点,由于它的函数值是唯一确定的常数,没有增减变化,所以不存在单调问题.因此写单调区间时,如果端点在定义域内,可以包括端点,也可以不包括端点,但对于某些点无意义时,单调区间就不包括这些点.
5.求函数的单调区间,就是求函数保持同一单调性不变的最大区间.
二、函数单调性的判断与证明
1.函数单调性的判断方法有三种:一是依据单调性的定义;二是依据函数的图象;三是依据已知函数的单调性判断.如已学过的一次函数、二次函数、反比例函数的单调性情况.
2.函数单调性的证明方法:
依据定义进行证明.其步骤如下:
①取值:即设x1,x2是该区间上的任意两个值,且x1
③定号:确定差f(x1)-f(x2)的符号,当符号不确定时,可以分情况讨论;
④判定:依据定义得出结论.
题型一 利用图象求函数的单调区间
【例1】 求下列函数的单调区间.
(1)f(x)=3|x|;
(2)f(x)=|x2+2x-3|.
典例剖析
f(x)在(-∞,0]上是减函数,在(0,+∞)上是增函数.
(2)令f(x)=x2+2x-3=(x+1)2-4.
先作出f(x)的图象,保留其在x轴及x轴上方部分,把它在x轴下方的图象翻到x轴上方就得到y=|x2+2x-3|的图象,如图所示.
由图象易得:函数的递增区间是(-3,-1),(1,+∞);
函数的递减区间是(-∞,-3],(-1,1].
点评:函数的单调区间可以是开的,也可以是闭的,也可以是半开半闭的,对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也单调.因此,只要单调区间端点使f(x)有意义,都可以使单调区间包括端点.但要注意,不连续的单调区间必须分开写,不能用“∪”符号连接它们.
1.求下列函数的单调区间
(2)f(x)=-x2+2|x|+3.
∴单调递增区间为(0,+∞),递减区间为(-∞,0).
(2)∵f(x)=-x2+2|x|+3
图象如图所示.
∴函数y=-x2+2|x|+3的单调递增区间为(-∞,-1],(0,1],递减区间为(-1,0],(1,+∞).
题型二 利用定义判定及证明函数单调性
点评:证明函数的单调性的常用方法是利用函数单调性的定义.其步骤为:(1)取值(注意x1、x2的任意性);(2)作差变形(目的是便于判断符号);(3)判断差的符号;(4)写出结论.
题型三 由函数的单调性求参数的取值范围
【例3】 已知函数f(x)=x2-2ax-3在区间[1,2]上单调,求实数a的取值范围.
解:函数f(x)=x2-2ax-3的图象开口向上,对称轴为直线x=a,画出草图如图所示.
由图象可知函数在(-∞,a]和(a,+∞)上分别单调,因此要使函数f(x)在区间[1,2]上单调,只需a≤1或a≥2(其中当a≤1时,函数f(x)在区间
[1,2]上单调递增;当a≥2时,函数f(x)在区间[1,2]上单调递减),从而a∈(-∞,1]∪ [2,+∞).
点评:已知函数的单调性求参数的取值范围,要注意数形结合思想,采用逆向思维.
3.已知函数f(x)=x2+2(a-1)x+2在区间 (-∞,4]上是减函数,求实数a的取值范围.
解:f(x)=x2+2(a-1)x+2
=[x+(a-1)]2-(a-1)2+2,
∴此二次函数的对称轴为x=1-a.
∴f(x)的单调减区间为(-∞,1-a].
∵f(x)在(-∞,4]上是减函数,
∴对称轴x=1-a必须在直线x=4的右侧或与其重合.
∴1-a≥4,解得a≤-3.
误区解密 因对“单调区间”和“区间上单调”
两个概念混淆而出错
【例4】 若函数f(x)=x2+2(a-1)x+2的单调递减区间是(-∞,4],则实数a的取值范围是______.
错解:函数f(x)的图象的对称轴为直线x=1-a,由于函数在区间(-∞,4]上单调递减,因此1-a≥4,即a≤-3.
错因分析:错解中把单调区间误认为是在区间上单调.
正解:因为函数的单调递减区间为(-∞,4],且函数图象的对称轴为直线x=1-a,所以有1-a=4,即a=-3.
答案:a=-3
纠错心得:单调区间是一个整体概念,比如说函数的单调递减区间是I,指的是函数递减的最大范围为区间I.而函数在某一区间上单调,则指此区间是相应单调区间的子集.所以我们在解决函数的单调性问题时,一定要仔细读题,明确条件含义.
1.函数的单调区间必须是定义域的子集.因此讨论函数的单调性时,必须先确定函数的定义域.
课堂总结
3.求单调区间的方法:(1)图象法;(2)定义法;(3)利用已知函数的单调性.
4.用单调性的定义证明函数的单调性分四个主要步骤:
即“取值——作差变形——定号——判断”这四个步骤.
