1.3.2《奇偶性1》课件(新人教A版必修1)
文档属性
| 名称 | 1.3.2《奇偶性1》课件(新人教A版必修1) |  | |
| 格式 | zip | ||
| 文件大小 | 8.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-17 04:31:55 | ||
图片预览







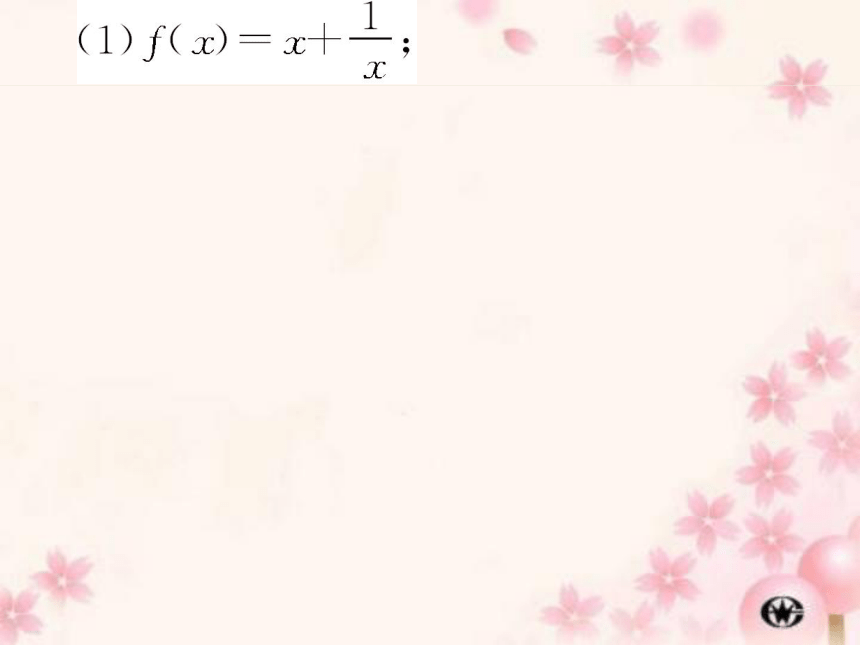




文档简介
(共38张PPT)
(深化、提高、巩固练习课)
请同学们课后再做好复习巩固.
谢谢!
再见!
1.3.2奇偶性
第一章
集合与函数概念
动9
P(x,y)
1.3
函数的基本性质
心甚础知识理
自主学习资实喜碰
J SHU
1.函数奇偶性的定义
1.函数奇偶性的定义
1)一般地,如果对于函数f(x)的定义域内
有
那么函数∫(x)就叫做偶函数
(2)一般地,如果对于函数f(x)的
内任意
都有
,那么函数f(x)就叫做奇函数
(-x)=f(
定义域
2.函数奇偶性的图象特征
2.函数奇偶性的图象特征
(1)如果一个函数是
这个函数的图象是以
原点为对称中心的中心对称图形;反之,如果一个刚数
图象是以
为对称中心的中心对称图形,则这个函数是奇
涵数
(2)如果一个函数是
刂它的图象是以y轴为对
称轴的轴对称图形;反之,如果
数的图象关于对
称,则这个函数是偶数
奇函数
原点
偶两数
心三基能力强化
颺化三薯譟前藏身
SANJINENGLIQIANGHUA
函数f(x)=又
的奇偶性为
奇凼数
B.偶函数
C.既奇又偶数
D.非奇非偶函数
答案:D
答案:D
下列结论中正确的是
偶函数的图象一定与y轴相交
B.奇函数y=f(x)在x=0处有定义,则f(0)=0
)图象一定过原点
D.图象过原点的奇函数必是单调函数
B
答案:B
数f(x)
,a>0,则必有
A fca(a
D f(a=f(
答案:B
答案:B
(x)是定义在R上的偶数,且当x≥0
答案
如果定义在区间
的函数f(x)为奇数,那
答案
答案:-x3+1
案:8
y课堂互动讲练]课
KETANCHUDONGIANGLIAN
题型
函数奇偶性的判断
题型
函数奇偶性的判断
例①》判断下列函数的奇偶
(1)f(x)
(2)f(x)
(3)f(x)
高考赘源网
高考资源
边的高考专家!】
【分析】先看函数的定义域是否关于原点对称,而后看
f(-x)与f(x)的关系或者从图上看图象是否关于原点或
y轴对称
解】(1)函数的定义域是{xx≠0},
所以关于原点对称
又f(-x)=-x+
f(a)
(3)法一:由
1≥0且1
0得
即函数的定义域为{-1,1},关于原点对称
又f(-1)=0=f(1),且f(-1)=-f(1)=0,
所以f(x)既是奇函数,又是偶函数
法二:因为函数的定义域为{—1,1},
画图象如右图所示
10
此函数图象只有两点,既关于原点对
称又关于y轴对称,此函数既是偶函数又是奇函数
(深化、提高、巩固练习课)
请同学们课后再做好复习巩固.
谢谢!
再见!
1.3.2奇偶性
第一章
集合与函数概念
动9
P(x,y)
1.3
函数的基本性质
心甚础知识理
自主学习资实喜碰
J SHU
1.函数奇偶性的定义
1.函数奇偶性的定义
1)一般地,如果对于函数f(x)的定义域内
有
那么函数∫(x)就叫做偶函数
(2)一般地,如果对于函数f(x)的
内任意
都有
,那么函数f(x)就叫做奇函数
(-x)=f(
定义域
2.函数奇偶性的图象特征
2.函数奇偶性的图象特征
(1)如果一个函数是
这个函数的图象是以
原点为对称中心的中心对称图形;反之,如果一个刚数
图象是以
为对称中心的中心对称图形,则这个函数是奇
涵数
(2)如果一个函数是
刂它的图象是以y轴为对
称轴的轴对称图形;反之,如果
数的图象关于对
称,则这个函数是偶数
奇函数
原点
偶两数
心三基能力强化
颺化三薯譟前藏身
SANJINENGLIQIANGHUA
函数f(x)=又
的奇偶性为
奇凼数
B.偶函数
C.既奇又偶数
D.非奇非偶函数
答案:D
答案:D
下列结论中正确的是
偶函数的图象一定与y轴相交
B.奇函数y=f(x)在x=0处有定义,则f(0)=0
)图象一定过原点
D.图象过原点的奇函数必是单调函数
B
答案:B
数f(x)
,a>0,则必有
A fca(a
D f(a=f(
答案:B
答案:B
(x)是定义在R上的偶数,且当x≥0
答案
如果定义在区间
的函数f(x)为奇数,那
答案
答案:-x3+1
案:8
y课堂互动讲练]课
KETANCHUDONGIANGLIAN
题型
函数奇偶性的判断
题型
函数奇偶性的判断
例①》判断下列函数的奇偶
(1)f(x)
(2)f(x)
(3)f(x)
高考赘源网
高考资源
边的高考专家!】
【分析】先看函数的定义域是否关于原点对称,而后看
f(-x)与f(x)的关系或者从图上看图象是否关于原点或
y轴对称
解】(1)函数的定义域是{xx≠0},
所以关于原点对称
又f(-x)=-x+
f(a)
(3)法一:由
1≥0且1
0得
即函数的定义域为{-1,1},关于原点对称
又f(-1)=0=f(1),且f(-1)=-f(1)=0,
所以f(x)既是奇函数,又是偶函数
法二:因为函数的定义域为{—1,1},
画图象如右图所示
10
此函数图象只有两点,既关于原点对
称又关于y轴对称,此函数既是偶函数又是奇函数
