鲁教版(五四制)八上4.4图形变化的简单应用 教案
文档属性
| 名称 | 鲁教版(五四制)八上4.4图形变化的简单应用 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 14:46:30 | ||
图片预览

文档简介
图形变化的简单应用
——教学设计
教学目标:
1.经历对生活中的典型图案进行观察、分析、欣赏等过程,认识和欣赏平移、旋转与轴对称在图形中的应用。
2.理解全等图形的简单变化,初步感受平移、旋转及轴对称的内在关系。
3.掌握对称中心的找法,并体会平移与轴对称,旋转与轴对称间的内在关系。
重点:经历观察、实验、操作的过程,分析图形之间的变换关系。
难点:综合运用几种变换分析图形,并用数学语言有条理地、清晰地描述自己的观点。
教学准备:课件,学生自制道具,教师自制道具。
学习过程:
1、情景引入,回顾旧知
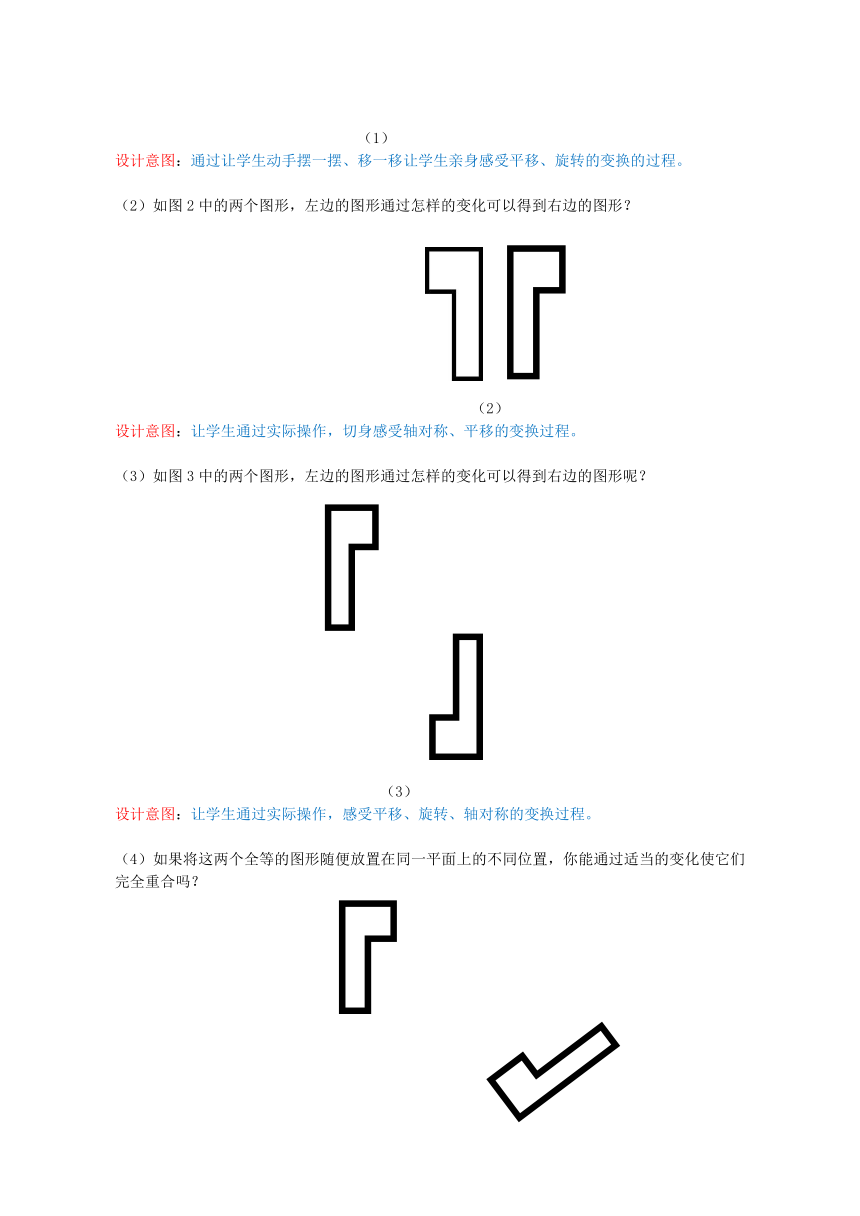
首先,课件出示了几幅美丽的图案,让学生找一找图片中有哪些数学中的图形变换。从而引出并回顾平移、旋转、轴对称的相关知识。
平移
旋转
轴对称
设计意图:通过几幅图片,让学生找图片中蕴含的图形变换,引起学生对本节课的兴趣。然后回顾平移、旋转、轴对称的相关知识,使学生对图形变换有整体的感知。
二、小试牛刀
1.观察下面各图,分别说明是怎样将△ABC变换到另一个与它全等的三角形的位置的。
设计意图:这几个问题比较简单,学生都明白,但学生会出现表达不清晰的问题。因此,本问题除了帮助学生回顾平移、旋转和轴对称的基本知识外,还要帮助学生规范语言表达。
三、团结协作(一)
(1)如图1中的两个图形,左边的图形通过怎样的变化可以得到右边的图形?
(1)
设计意图:通过让学生动手摆一摆、移一移让学生亲身感受平移、旋转的变换的过程。
(2)如图2中的两个图形,左边的图形通过怎样的变化可以得到右边的图形?
(2)
设计意图:让学生通过实际操作,切身感受轴对称、平移的变换过程。
(3)如图3中的两个图形,左边的图形通过怎样的变化可以得到右边的图形呢?
(3)
设计意图:让学生通过实际操作,感受平移、旋转、轴对称的变换过程。
(4)如果将这两个全等的图形随便放置在同一平面上的不同位置,你能通过适当的变化使它们完全重合吗?
(4)
设计意图:在前面三个探究问题的基础上提出设想,把道具任意位置摆放,让学生进行适当变换,使得两个全等图形重合。加大了图形变换的难度,从而加深学生对图形变换的相关感受。
交流提升
(1)任意两个全等图形都能通过图形变化使它们重合吗?
(2)两个全等图形都能通过一次图形变化使它们重合吗?
(3)两个全等图形可以通过一次图形变化得到或多次图形变化得到时,你觉得哪种方法更好?
设计意图:学生在前面进行了充分的合作探究,对图形变换有了很多感受,思维也比较发散。但他们得感受“乱而无序”“天马行空”,这几个问题就是要把他们得思想收回来,通过这几个问题的交流让他们得感受更清晰,更具体。
团结协作(二)
1.
在图(1)中先做出△ABC关于直线l的轴对称图形△ABC,再做△ABC关于l的轴对称图形△ABC.观察△ABC和△ABC,你有什么发现?
2.在图(2)中先做出△ABC关于直线l的轴对称图形△ABC,再做△ABC关于l的轴对称图形△ABC.观察△ABC和△ABC,你有什么发现?
设计意图:本环节旨在让学生从动手摆一摆的整体感受转变为让学生动手画一画的具体感知。更深刻的体会一步变换和多步变换之间的内在联系。
变换应用
1、如图所示,AB是长为4的线段,且CD⊥AB于O。你能求出图中阴影部分的面积吗?说说你的做法。
设计意图:让学生通过解决具体的数学问题,从而对图形变换的应用更广泛,进而产生对图形变换感悟的升华。
小结:出示情景引入的图片,让学生说一说,这幅图片是怎么设计的?
设计意图:这个环节是对情景引入的照应,在情景引入时让学生找出图片里的一些图形变换,而本环节是让学生思考说出图片是怎么设计出来的,是本节课学习的升华。
请你欣赏:下图是我用几何画板利用平移、旋转、轴对称绘制的图形。
设计意图:本环节是在本节课的最后半分钟利用几何画板给学生演示图片的生成过程。旨在抛砖引玉,激发学生设计出更加漂亮的图案。
平移
旋转
轴对称
——教学设计
教学目标:
1.经历对生活中的典型图案进行观察、分析、欣赏等过程,认识和欣赏平移、旋转与轴对称在图形中的应用。
2.理解全等图形的简单变化,初步感受平移、旋转及轴对称的内在关系。
3.掌握对称中心的找法,并体会平移与轴对称,旋转与轴对称间的内在关系。
重点:经历观察、实验、操作的过程,分析图形之间的变换关系。
难点:综合运用几种变换分析图形,并用数学语言有条理地、清晰地描述自己的观点。
教学准备:课件,学生自制道具,教师自制道具。
学习过程:
1、情景引入,回顾旧知
首先,课件出示了几幅美丽的图案,让学生找一找图片中有哪些数学中的图形变换。从而引出并回顾平移、旋转、轴对称的相关知识。
平移
旋转
轴对称
设计意图:通过几幅图片,让学生找图片中蕴含的图形变换,引起学生对本节课的兴趣。然后回顾平移、旋转、轴对称的相关知识,使学生对图形变换有整体的感知。
二、小试牛刀
1.观察下面各图,分别说明是怎样将△ABC变换到另一个与它全等的三角形的位置的。
设计意图:这几个问题比较简单,学生都明白,但学生会出现表达不清晰的问题。因此,本问题除了帮助学生回顾平移、旋转和轴对称的基本知识外,还要帮助学生规范语言表达。
三、团结协作(一)
(1)如图1中的两个图形,左边的图形通过怎样的变化可以得到右边的图形?
(1)
设计意图:通过让学生动手摆一摆、移一移让学生亲身感受平移、旋转的变换的过程。
(2)如图2中的两个图形,左边的图形通过怎样的变化可以得到右边的图形?
(2)
设计意图:让学生通过实际操作,切身感受轴对称、平移的变换过程。
(3)如图3中的两个图形,左边的图形通过怎样的变化可以得到右边的图形呢?
(3)
设计意图:让学生通过实际操作,感受平移、旋转、轴对称的变换过程。
(4)如果将这两个全等的图形随便放置在同一平面上的不同位置,你能通过适当的变化使它们完全重合吗?
(4)
设计意图:在前面三个探究问题的基础上提出设想,把道具任意位置摆放,让学生进行适当变换,使得两个全等图形重合。加大了图形变换的难度,从而加深学生对图形变换的相关感受。
交流提升
(1)任意两个全等图形都能通过图形变化使它们重合吗?
(2)两个全等图形都能通过一次图形变化使它们重合吗?
(3)两个全等图形可以通过一次图形变化得到或多次图形变化得到时,你觉得哪种方法更好?
设计意图:学生在前面进行了充分的合作探究,对图形变换有了很多感受,思维也比较发散。但他们得感受“乱而无序”“天马行空”,这几个问题就是要把他们得思想收回来,通过这几个问题的交流让他们得感受更清晰,更具体。
团结协作(二)
1.
在图(1)中先做出△ABC关于直线l的轴对称图形△ABC,再做△ABC关于l的轴对称图形△ABC.观察△ABC和△ABC,你有什么发现?
2.在图(2)中先做出△ABC关于直线l的轴对称图形△ABC,再做△ABC关于l的轴对称图形△ABC.观察△ABC和△ABC,你有什么发现?
设计意图:本环节旨在让学生从动手摆一摆的整体感受转变为让学生动手画一画的具体感知。更深刻的体会一步变换和多步变换之间的内在联系。
变换应用
1、如图所示,AB是长为4的线段,且CD⊥AB于O。你能求出图中阴影部分的面积吗?说说你的做法。
设计意图:让学生通过解决具体的数学问题,从而对图形变换的应用更广泛,进而产生对图形变换感悟的升华。
小结:出示情景引入的图片,让学生说一说,这幅图片是怎么设计的?
设计意图:这个环节是对情景引入的照应,在情景引入时让学生找出图片里的一些图形变换,而本环节是让学生思考说出图片是怎么设计出来的,是本节课学习的升华。
请你欣赏:下图是我用几何画板利用平移、旋转、轴对称绘制的图形。
设计意图:本环节是在本节课的最后半分钟利用几何画板给学生演示图片的生成过程。旨在抛砖引玉,激发学生设计出更加漂亮的图案。
平移
旋转
轴对称
