鲁教版(五四制)八上5.2.2平行四边形的判定 教案(表格式)
文档属性
| 名称 | 鲁教版(五四制)八上5.2.2平行四边形的判定 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览


文档简介
第五章《平行四边形的判定2——利用一组对边关系》教学设计
课题
5.2.1
平行四边形的判定
学情分析
学生知识技能基础:学生在小学已经学行四边形,对平行四边形有直观的感知和认识。在第一节也学行四边形的性质,同时通过定义学生也已经获得了1种判定平行四边形的方法,第二节学生也学习了通过两组对边分别相等判定平行四边形,这节课继续探究平行四边形的判定方法。
学生活动经验基础:在掌握平行线和相交线的性质,以及三角形全等的性质和判定,平行四边形性质等几何知识和的前提下,学生已经初步经历过观察、操作等活动过程,获得了一定的探索图形性质的活动经验;同时,在学习数学的过程中也经历了很多合作过程,具有了一定的学习经验,具备了一定的合作和交流能力
教学目标
知识技能
1.通过学生的合作探究,得出平行四边形的判别方法。
2.理解平行四边形的一组对边平行且相等判定方法,并学会简单运用。
过程与方法
1.探索平行四边形的判定条件的过程,在实践操作、观察、猜想、证明等数学活动过程,发展学生合情推理能力和演绎推理能力。
2.通过师生互动,生生互动、学生自主探究和小组讨论的形式解决问题。
情感态度与价值观
1.通过对平行四边形判定方法的探究和运用,使学生感受数学思考过程中的合理性、数学证明的严谨性,认识事物间的相互联系、相互转化,学会用辩证的观点分析事物;
2.培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情。
3.引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并
在运用数学知识解答问题的活动中获取成功的体验,建立学习的信
心。
重点
平行四边形的判定方法2及证明及应用
难点
平行四边形的性质与判定的综合应用
教学过程设计
问题与情境
师生行为
设计意图
复习引入
设问:
我们前面学习了几种判定平行四边形的方法?
2.参照图形,我们一起用几何语言表述一下(学生回答老师板书)
3今天我们将继续探究平行四边形的判定方法.
二.新知探究
1.探究:给你两根长度相等的木棒,在平面内怎么摆放才能使它们的四个端点恰好是一个平行四边形的顶点?(小组活动交流再用投影仪展示)
作品1:交叉摆放,两根木棒的交点便是每根木棒的中点——留到下节课探究
作品2:两根木棒平行摆放
问1:这两根木棒除了这种位置关系,还有什么关系?
问2:你能不能概括一下,满足什么条件摆放的图形是平行四边形?
学生得出猜想的命题并证明
【命题证明】
命题:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD,AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵AB∥CD
∴∠ABD=∠CDB
又∵AB=CD,BD=BD
∴ΔABD≌ΔCDB
∴AD=CD
∴四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形
(把刚刚的证明命题转化为几何语言)
问:还可以通过哪一组对边平行且相等来判定平行四边形(学生口述老师板书)
三.新知应用
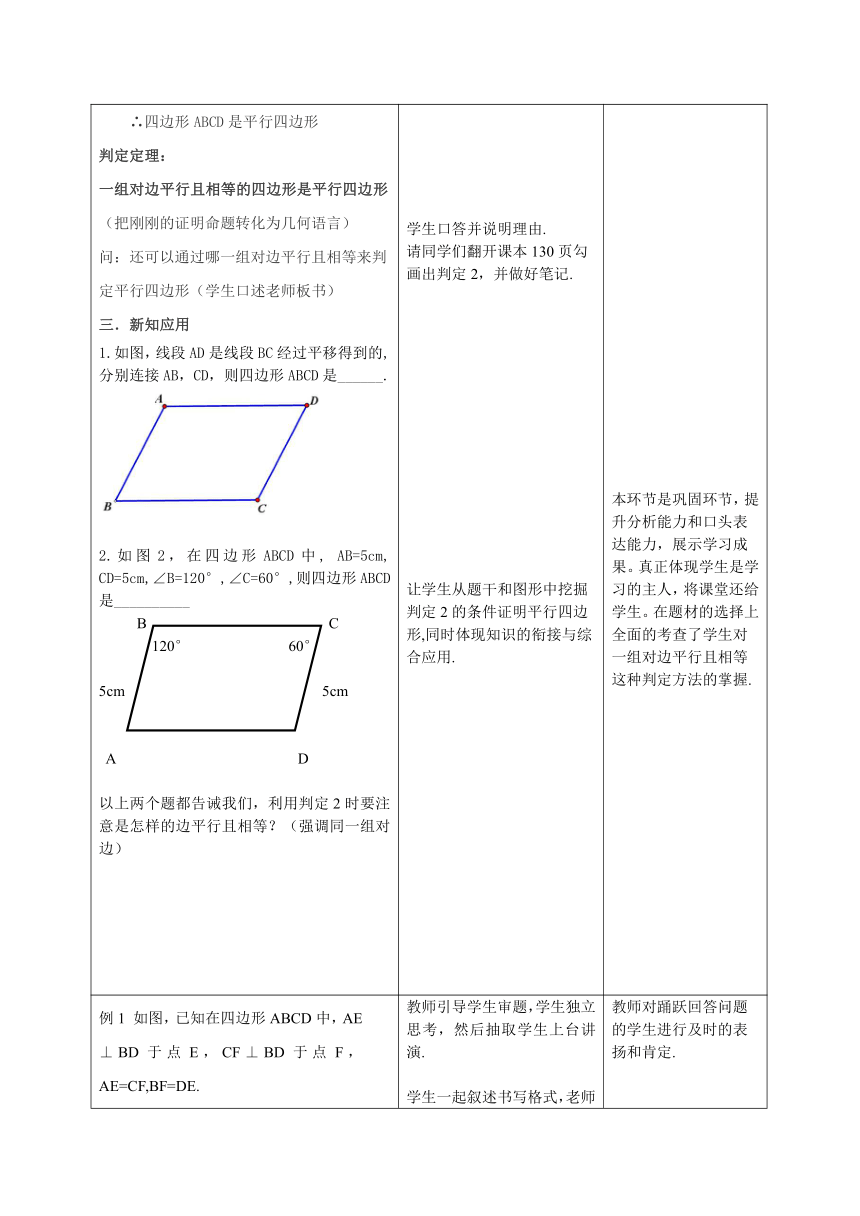
1.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,则四边形ABCD是______.
2.如图2,在四边形ABCD中,
AB=5cm,
CD=5cm,∠B=120°,∠C=60°,则四边形ABCD是__________
B
C
120°
60°
5cm
5cm
A
D
以上两个题都告诫我们,利用判定2时要注意是怎样的边平行且相等?(强调同一组对边)
教师带着同学回顾平行四边形的判定.
老师抛出问题,学生动手操作,小组讨论,激发学生的探究兴趣.
小组总结汇报:做法和猜想.
同学们通过动手操作的过程,总结判定平行四边形的方法,其中定义法的正确性不需验证,其他的方法正确性和可行性我们将一一验证,本节课我们选择一种方法来验证,其他的下节课继续探究.
学生独立思考,解决问题,教师展示其中一种证明方法的解题格式.
学生口答并说明理由.
请同学们翻开课本130页勾画出判定2,并做好笔记.
让学生从题干和图形中挖掘判定2的条件证明平行四边形,同时体现知识的衔接与综合应用.
带领学生站在平面几何图形研究的一般历程:
(定义
性质
判定
运用)高度上进入研究的主题。便于学生形成对几何研究的方向的把握.
让学生动手操作,体会新知识的形成过程,总结平行四边形的判定2.
本环节是本节课重点内容.
老师的对学生的猜想实时的给予肯定,有助于增强学生学习的信心,活跃课堂气氛.
通过实践活动和合作交流,猜想并证明平行四边形的一个判定定理,突出本节课的重难点,点明本节课主旨.
本环节是巩固环节,提升分析能力和口头表达能力,展示学习成果。真正体现学生是学习的主人,将课堂还给学生。在题材的选择上全面的考查了学生对一组对边平行且相等这种判定方法的掌握.
例1
如图,已知在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BF=DE.
求证:四边形ABCD是平行四边形.
问:哪位同学愿意分享一下方法?
问:还有其他方法吗?
问:这些方法哪种最简单呢?
追问:连接AF、CE,则四边形AECF是什么四边形?
变式1
如图,已知在平行四边形ABCD中,
BF=DE,连接AE,CF.
求证:四边形AFCE是平行四边形.
问:谁自告奋勇的展示一下你的解题方法?
问:你能将这道题变式吗?尝试一下
(展示学生变式的图形,并作为课后作业)
变式2
如图,在平行四边形ABCD中,点M,N分别在AD和BC上,点E,F在BD上,AM=CN,BF=DE.
求证:四边形MENF是平行四边形.
问:哪位同学愿意展示自己的解答格式?
问:请其他同学检查一下,在格式上有没有需要改进的地方?
问:还有没有其他方法?小组间讨论一下
追问:若平行四边形ABCD的面积为16,
则S△ENF+S△MFB+S四边形ADEM=_____________.
问:现在你们有几种判定平行四边形的方法?下面我们利用这种方法在网格图中画出平行四边形?
四.数学操作
如图,以方格纸的格点为顶点用直尺画一个平行四边形,并说明你画图的方法和其中的道理.
五.课后小结
问:1、本节课你有哪些收获?
2、你还有哪些疑惑?
数学知识
数学思想
大家都很棒,擅于归纳总结,并学以致用,解决困惑.其实我们的数学与生活紧密相连,所学的数学知识也可以服务于生活:
六.作业布置
选做题:王强同学不小心碰碎了实验室的一块平行四边形玻璃,剩下部分如图,他要去买一块同样形状大小的玻璃赔给学校,你能帮他画出原来的图形吗?
必做题
1、如图,已知在平行四边形ABCD中,
E、F在BD的延长线上,
AE=CF,BF=DE.
求证:四边形AECF是平行四边形.
2、教材132页第1、2、4题.
思考:在新知探究过程中,两根相等的木棒交叉摆放,四个端点能否构成平行四边形的四个顶点?
教师引导学生审题,学生独立思考,然后抽取学生上台讲演.
学生一起叙述书写格式,老师板书.
可利用定义,或判定1,判定2证明。但可从多种策略中选择最简单、最有效的途径解决问题。同时让学生体会如何通过已知条件迅速的寻求解题方法.
学生独立思考,审题,分析,解决问题.在学生的回答过程中,追问还可以如何创造这两条线段平行的条件.让学生自己挖掘出题干隐藏的条件:
∵BF=DE
∴BF+EF=DE+EF
即BE=DF
老师引导学生审题,让学生挖掘隐藏的条件:
①∵AM=NC,AB=DC
∴AB-AM=DC-NC
即BM=DN
②∵BF=DE
∴BF+EF=DE+EF
即BE=DF
随机抽取学生,展示学生的书写格式,请其他同学检查书写格式.
即时小结方法:一题多解和一题多变。让学生感受到“作一题通一类”。
用三种判定方法画平行四边形,作动手操作过程中,形成知识框架:如何判定平行四边形。同时将现在的知识与小学的知识进行衔接.
学生畅所欲言环节,及时了解学生的学习状态,反馈课堂实效.
引导学生自己总结知识和数学思想。教师对学生总结的知识点给予重现,及时解答学生困惑.
学生根据新知解决课堂引入时的问题:两条木棒交叉摆放,使得交点分别是每根木棒的中点.
适当练习,巩固新知
教师对踊跃回答问题的学生进行及时的表扬和肯定.
让学生自主的将题干中的条件转化为判定方法需要的条件,体会数学转化思想.
重视几何证明的书写格式。抽取学生的答题,学生互相纠错更正,然后小组互助合作和交流,达到全部过关的理想目标.
培养学生分析问题,解决问题能力以及知识的应用能力.
平行四边形的性质与判定的简单结合.
通过作图形这个数学活动来放松学生的大脑,提高学生的学习积极性.
学生对本节课所学内容的归纳、总结,帮助学生建构起比较完善的知识结构,归纳数学学习中常用的思想方法,从而提高他们自主学习、独立学习的能力。
培养学生养成反思习惯、提高归纳能力、体会数学思想.
着重检查学生的书写格式
让学生体会到数学来源于生活,同时又服务于生活,从而提高学生学习的积极性
分层次布置作业,让不同层次的学生的数学能力得到提升。
教学反思
平行四边形的判定这一节课堂容量大,所以本节课我采用
“几何问题→实际问题→实践活动→
思考交流→归纳性质→解决问题”的模式。给学生创建平等、轻松和谐的学习氛围,让学生的个性得到张扬,形成师生互动、生生互动的学习环境,学生积极参与每个环节的学习活动,积极回答问题,课堂气氛活跃,学生思维活跃,使我们的课堂走向精彩。本节课从总体上看,学生基本掌握了平行四边形的判定方法的运用,较好的完成了教学目的。但教无定法,我们只有以发展的眼光看待我们的孩子,不断改进我们的教学,才能实现真正意义上的让学生作学习的主人。
课题
5.2.1
平行四边形的判定
学情分析
学生知识技能基础:学生在小学已经学行四边形,对平行四边形有直观的感知和认识。在第一节也学行四边形的性质,同时通过定义学生也已经获得了1种判定平行四边形的方法,第二节学生也学习了通过两组对边分别相等判定平行四边形,这节课继续探究平行四边形的判定方法。
学生活动经验基础:在掌握平行线和相交线的性质,以及三角形全等的性质和判定,平行四边形性质等几何知识和的前提下,学生已经初步经历过观察、操作等活动过程,获得了一定的探索图形性质的活动经验;同时,在学习数学的过程中也经历了很多合作过程,具有了一定的学习经验,具备了一定的合作和交流能力
教学目标
知识技能
1.通过学生的合作探究,得出平行四边形的判别方法。
2.理解平行四边形的一组对边平行且相等判定方法,并学会简单运用。
过程与方法
1.探索平行四边形的判定条件的过程,在实践操作、观察、猜想、证明等数学活动过程,发展学生合情推理能力和演绎推理能力。
2.通过师生互动,生生互动、学生自主探究和小组讨论的形式解决问题。
情感态度与价值观
1.通过对平行四边形判定方法的探究和运用,使学生感受数学思考过程中的合理性、数学证明的严谨性,认识事物间的相互联系、相互转化,学会用辩证的观点分析事物;
2.培养学生面对挑战,勇于克服困难的意志,鼓励学生大胆尝试,从中获得成功的体验,激发学生的学习热情。
3.引导学生对图形的观察、发现,激发学生的好奇心和求知欲,并
在运用数学知识解答问题的活动中获取成功的体验,建立学习的信
心。
重点
平行四边形的判定方法2及证明及应用
难点
平行四边形的性质与判定的综合应用
教学过程设计
问题与情境
师生行为
设计意图
复习引入
设问:
我们前面学习了几种判定平行四边形的方法?
2.参照图形,我们一起用几何语言表述一下(学生回答老师板书)
3今天我们将继续探究平行四边形的判定方法.
二.新知探究
1.探究:给你两根长度相等的木棒,在平面内怎么摆放才能使它们的四个端点恰好是一个平行四边形的顶点?(小组活动交流再用投影仪展示)
作品1:交叉摆放,两根木棒的交点便是每根木棒的中点——留到下节课探究
作品2:两根木棒平行摆放
问1:这两根木棒除了这种位置关系,还有什么关系?
问2:你能不能概括一下,满足什么条件摆放的图形是平行四边形?
学生得出猜想的命题并证明
【命题证明】
命题:一组对边平行且相等的四边形是平行四边形
已知:AB∥CD,AB=CD
求证:四边形ABCD是平行四边形
证明:连接BD
∵AB∥CD
∴∠ABD=∠CDB
又∵AB=CD,BD=BD
∴ΔABD≌ΔCDB
∴AD=CD
∴四边形ABCD是平行四边形
判定定理:
一组对边平行且相等的四边形是平行四边形
(把刚刚的证明命题转化为几何语言)
问:还可以通过哪一组对边平行且相等来判定平行四边形(学生口述老师板书)
三.新知应用
1.如图,线段AD是线段BC经过平移得到的,分别连接AB,CD,则四边形ABCD是______.
2.如图2,在四边形ABCD中,
AB=5cm,
CD=5cm,∠B=120°,∠C=60°,则四边形ABCD是__________
B
C
120°
60°
5cm
5cm
A
D
以上两个题都告诫我们,利用判定2时要注意是怎样的边平行且相等?(强调同一组对边)
教师带着同学回顾平行四边形的判定.
老师抛出问题,学生动手操作,小组讨论,激发学生的探究兴趣.
小组总结汇报:做法和猜想.
同学们通过动手操作的过程,总结判定平行四边形的方法,其中定义法的正确性不需验证,其他的方法正确性和可行性我们将一一验证,本节课我们选择一种方法来验证,其他的下节课继续探究.
学生独立思考,解决问题,教师展示其中一种证明方法的解题格式.
学生口答并说明理由.
请同学们翻开课本130页勾画出判定2,并做好笔记.
让学生从题干和图形中挖掘判定2的条件证明平行四边形,同时体现知识的衔接与综合应用.
带领学生站在平面几何图形研究的一般历程:
(定义
性质
判定
运用)高度上进入研究的主题。便于学生形成对几何研究的方向的把握.
让学生动手操作,体会新知识的形成过程,总结平行四边形的判定2.
本环节是本节课重点内容.
老师的对学生的猜想实时的给予肯定,有助于增强学生学习的信心,活跃课堂气氛.
通过实践活动和合作交流,猜想并证明平行四边形的一个判定定理,突出本节课的重难点,点明本节课主旨.
本环节是巩固环节,提升分析能力和口头表达能力,展示学习成果。真正体现学生是学习的主人,将课堂还给学生。在题材的选择上全面的考查了学生对一组对边平行且相等这种判定方法的掌握.
例1
如图,已知在四边形ABCD中,AE⊥BD于点E,CF⊥BD于点F,AE=CF,BF=DE.
求证:四边形ABCD是平行四边形.
问:哪位同学愿意分享一下方法?
问:还有其他方法吗?
问:这些方法哪种最简单呢?
追问:连接AF、CE,则四边形AECF是什么四边形?
变式1
如图,已知在平行四边形ABCD中,
BF=DE,连接AE,CF.
求证:四边形AFCE是平行四边形.
问:谁自告奋勇的展示一下你的解题方法?
问:你能将这道题变式吗?尝试一下
(展示学生变式的图形,并作为课后作业)
变式2
如图,在平行四边形ABCD中,点M,N分别在AD和BC上,点E,F在BD上,AM=CN,BF=DE.
求证:四边形MENF是平行四边形.
问:哪位同学愿意展示自己的解答格式?
问:请其他同学检查一下,在格式上有没有需要改进的地方?
问:还有没有其他方法?小组间讨论一下
追问:若平行四边形ABCD的面积为16,
则S△ENF+S△MFB+S四边形ADEM=_____________.
问:现在你们有几种判定平行四边形的方法?下面我们利用这种方法在网格图中画出平行四边形?
四.数学操作
如图,以方格纸的格点为顶点用直尺画一个平行四边形,并说明你画图的方法和其中的道理.
五.课后小结
问:1、本节课你有哪些收获?
2、你还有哪些疑惑?
数学知识
数学思想
大家都很棒,擅于归纳总结,并学以致用,解决困惑.其实我们的数学与生活紧密相连,所学的数学知识也可以服务于生活:
六.作业布置
选做题:王强同学不小心碰碎了实验室的一块平行四边形玻璃,剩下部分如图,他要去买一块同样形状大小的玻璃赔给学校,你能帮他画出原来的图形吗?
必做题
1、如图,已知在平行四边形ABCD中,
E、F在BD的延长线上,
AE=CF,BF=DE.
求证:四边形AECF是平行四边形.
2、教材132页第1、2、4题.
思考:在新知探究过程中,两根相等的木棒交叉摆放,四个端点能否构成平行四边形的四个顶点?
教师引导学生审题,学生独立思考,然后抽取学生上台讲演.
学生一起叙述书写格式,老师板书.
可利用定义,或判定1,判定2证明。但可从多种策略中选择最简单、最有效的途径解决问题。同时让学生体会如何通过已知条件迅速的寻求解题方法.
学生独立思考,审题,分析,解决问题.在学生的回答过程中,追问还可以如何创造这两条线段平行的条件.让学生自己挖掘出题干隐藏的条件:
∵BF=DE
∴BF+EF=DE+EF
即BE=DF
老师引导学生审题,让学生挖掘隐藏的条件:
①∵AM=NC,AB=DC
∴AB-AM=DC-NC
即BM=DN
②∵BF=DE
∴BF+EF=DE+EF
即BE=DF
随机抽取学生,展示学生的书写格式,请其他同学检查书写格式.
即时小结方法:一题多解和一题多变。让学生感受到“作一题通一类”。
用三种判定方法画平行四边形,作动手操作过程中,形成知识框架:如何判定平行四边形。同时将现在的知识与小学的知识进行衔接.
学生畅所欲言环节,及时了解学生的学习状态,反馈课堂实效.
引导学生自己总结知识和数学思想。教师对学生总结的知识点给予重现,及时解答学生困惑.
学生根据新知解决课堂引入时的问题:两条木棒交叉摆放,使得交点分别是每根木棒的中点.
适当练习,巩固新知
教师对踊跃回答问题的学生进行及时的表扬和肯定.
让学生自主的将题干中的条件转化为判定方法需要的条件,体会数学转化思想.
重视几何证明的书写格式。抽取学生的答题,学生互相纠错更正,然后小组互助合作和交流,达到全部过关的理想目标.
培养学生分析问题,解决问题能力以及知识的应用能力.
平行四边形的性质与判定的简单结合.
通过作图形这个数学活动来放松学生的大脑,提高学生的学习积极性.
学生对本节课所学内容的归纳、总结,帮助学生建构起比较完善的知识结构,归纳数学学习中常用的思想方法,从而提高他们自主学习、独立学习的能力。
培养学生养成反思习惯、提高归纳能力、体会数学思想.
着重检查学生的书写格式
让学生体会到数学来源于生活,同时又服务于生活,从而提高学生学习的积极性
分层次布置作业,让不同层次的学生的数学能力得到提升。
教学反思
平行四边形的判定这一节课堂容量大,所以本节课我采用
“几何问题→实际问题→实践活动→
思考交流→归纳性质→解决问题”的模式。给学生创建平等、轻松和谐的学习氛围,让学生的个性得到张扬,形成师生互动、生生互动的学习环境,学生积极参与每个环节的学习活动,积极回答问题,课堂气氛活跃,学生思维活跃,使我们的课堂走向精彩。本节课从总体上看,学生基本掌握了平行四边形的判定方法的运用,较好的完成了教学目的。但教无定法,我们只有以发展的眼光看待我们的孩子,不断改进我们的教学,才能实现真正意义上的让学生作学习的主人。
