鲁教版(五四制)九上2.1.1 锐角三角函数-正切 教案
文档属性
| 名称 | 鲁教版(五四制)九上2.1.1 锐角三角函数-正切 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 114.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 15:57:24 | ||
图片预览


文档简介
锐角三角函数(第一课时)
学习目标
经历刻画梯子倾斜程度的过程,能理解正切的使用意义,能说出一个锐角的正切的表示方法,感受正切在生活中的应用。
在探究的过程中感受转化,数形结合,特殊到一般等数学思想在解决问题中的应用。
评价任务
能够清晰说出一个锐角的正切以及正切表示物体倾斜程度。
根据课堂上的活动说出在这个过程中体现的数学思想方法。
学习重点难点
重点:用正切表示物体倾斜程度。
难点:理解为什么正切可以表示物体的倾斜程度。
学习过程
导入新课
在生活中我们常常需要表示物体的倾斜程度。如:梯子,楼梯等(多媒体展示生活图片),对于物体的倾斜程度你有哪些生活体验呢?(学生通过生活经验说一说对物体倾斜程度的感受)那么你知道数学上是怎么刻画物体的倾斜程度的吗?今天我们就一起深入学习一下。
探索新知
1.引入探究
以梯子为例,如何比较两个梯子的倾斜程度?
生1:可以看梯子与地面的夹角,也就是梯子的倾斜角,倾斜角大的梯子就陡。
师:这是个好方法,很直接。但是我们知道在生活中有时测量角度会比较困难,有没有其他的方法呢?
生2:角度不行可以用长度嘛,同一个梯子,梯子底端到墙角的距离近,梯子就陡,梯子顶端到墙角的距离远,梯子就陡。
师:非常好,这位同学用到了转化的数学思想方法,同时这也说明了操作方法。那么我们就根据长度尝试一下表示物体的倾斜程度。
2.探究新知
如图,你能比较梯子的倾斜程度吗?
问题1:你准备怎么解决这个问题?小组内讨论1分钟
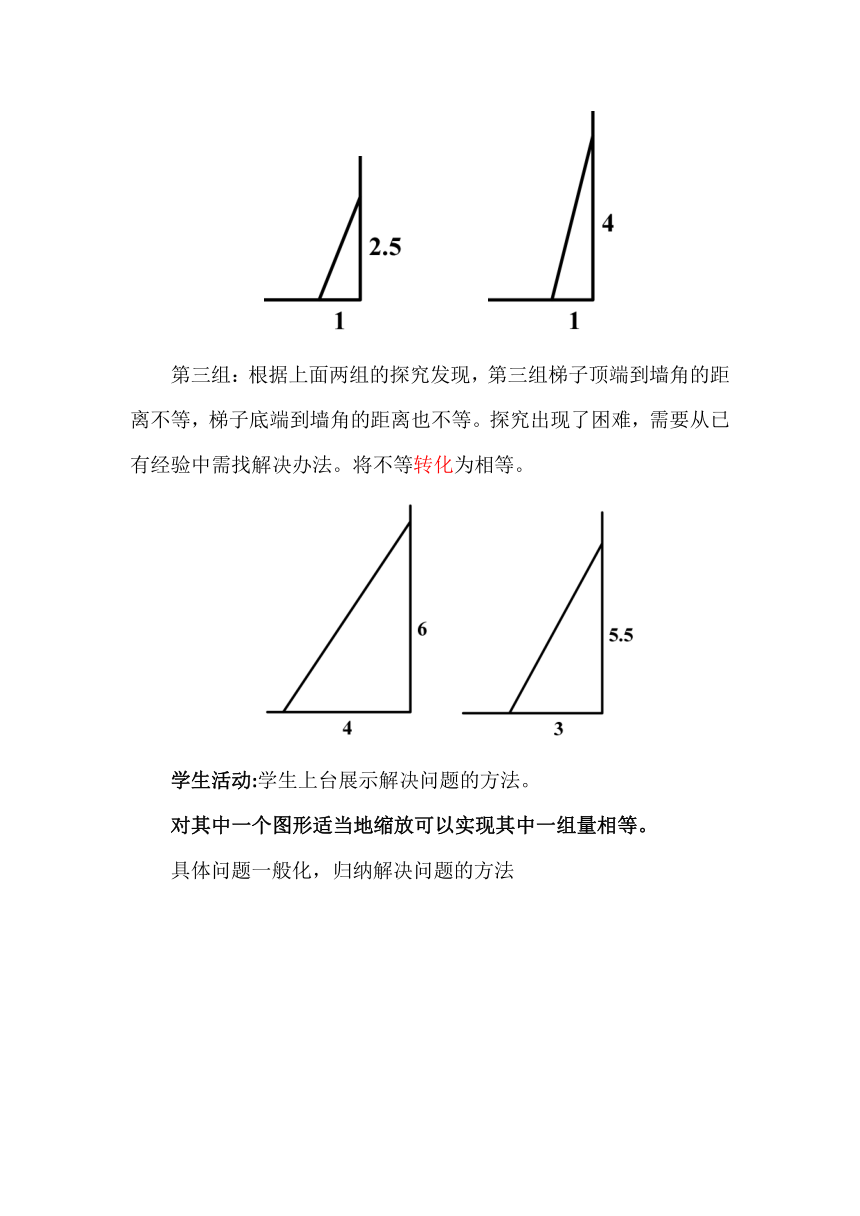
第一组的共同特征是:梯子顶端到墙角的距离相等。比较梯子底端到墙角的距离就可判断梯子的倾斜程度。
第二组的共同特征是:梯子底端到墙角的距离相等。比较梯子顶端到墙角的距离就可以判断梯子的倾斜程度。
第三组:根据上面两组的探究发现,第三组梯子顶端到墙角的距离不等,梯子底端到墙角的距离也不等。探究出现了困难,需要从已有经验中需找解决办法。将不等转化为相等。
学生活动:学生上台展示解决问题的方法。
对其中一个图形适当地缩放可以实现其中一组量相等。
具体问题一般化,归纳解决问题的方法
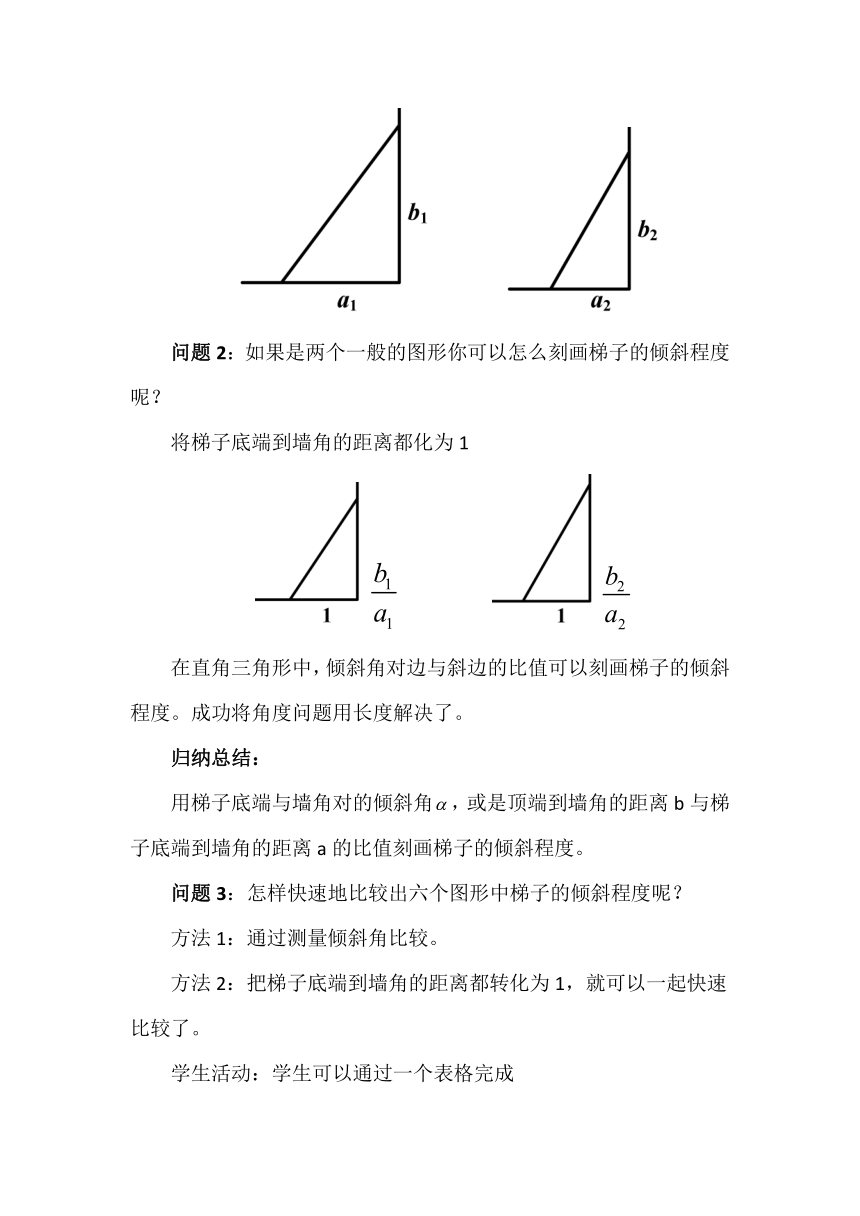
问题2:如果是两个一般的图形你可以怎么刻画梯子的倾斜程度呢?
将梯子底端到墙角的距离都化为1
在直角三角形中,倾斜角对边与斜边的比值可以刻画梯子的倾斜程度。成功将角度问题用长度解决了。
归纳总结:
用梯子底端与墙角对的倾斜角,或是顶端到墙角的距离b与梯子底端到墙角的距离a的比值刻画梯子的倾斜程度。
问题3:怎样快速地比较出六个图形中梯子的倾斜程度呢?
方法1:通过测量倾斜角比较。
方法2:把梯子底端到墙角的距离都转化为1,就可以一起快速比较了。
学生活动:学生可以通过一个表格完成
①
②
③
④
⑤
⑥
倾斜角
总结探索结论
倾斜角和都能刻画梯子的倾斜程度,它们是对应的关系,是一种函数关系。
特殊到一般
问题4:你能表示上图斜坡的倾斜程度吗?
缺少直角三角形,需要构造直角三角形,能够构造出很多直角三角形,就会发现这些直角三角形都是相似的,因此得到在直角三角形中倾斜角的对边与邻边的比值只与倾斜角的大小有关。给出正切的概念。
正切的概念
在中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
总结:倾斜角越大,tanA的值越大,梯子越陡。
给出一个倾斜角就有唯一一个比值tan与它对应,tan是倾斜角的函数,这种刻画三角形边角关系的函数称为三角函数,是倾斜角的正切函数。
同步练习
1.如图,甲乙两个自动扶梯,哪一个自动扶梯比较陡?
2.如图,某人从山脚下的点A走了200m后到达山顶的点B,已知点B到山脚的垂直距离为55m,求山的坡度(结果精确到0.01)
课堂小结
教师的小结
通过本节课的探索学习总结数学思想方法有:转化,特殊到一般,数形结合等。
学生的小结
1.通过本节课的学习在学习方法上你有什么收获?
2.在知识上你有什么收获?
板书设计
三角函数-正切
倾斜角
①
②
③
④
⑤
⑥
倾斜角
倾斜角∠A越大,tanA的值越大,梯子越陡。
教学反思
通过本节课针对本人的教学设计和课堂实施情况进行总结其中处理的特别好的环节有以下几点:1.在探索高度和宽度都不等的两个梯子的倾斜程度的时候,学生的活动时间比较多,充分展示了学生的思维成果,体现了学生的主体作用。2.对于为什么倾斜角的正切值可以表示梯子的倾斜程度,学生在探究的过程中有了自己的理解。3.学生对于三角函数这个抽象的概念也通过函数
的变量对应学生有了清楚的理解。课堂上存在的不足有:学生的对应练习时间有些不足。
通过本节课我的收获有:1.给学生充分表达自己想法的机会,学生会给教师很多的惊喜。2.关注知识的由来和发生过程,学生对知识的理解会更深刻。
学习目标
经历刻画梯子倾斜程度的过程,能理解正切的使用意义,能说出一个锐角的正切的表示方法,感受正切在生活中的应用。
在探究的过程中感受转化,数形结合,特殊到一般等数学思想在解决问题中的应用。
评价任务
能够清晰说出一个锐角的正切以及正切表示物体倾斜程度。
根据课堂上的活动说出在这个过程中体现的数学思想方法。
学习重点难点
重点:用正切表示物体倾斜程度。
难点:理解为什么正切可以表示物体的倾斜程度。
学习过程
导入新课
在生活中我们常常需要表示物体的倾斜程度。如:梯子,楼梯等(多媒体展示生活图片),对于物体的倾斜程度你有哪些生活体验呢?(学生通过生活经验说一说对物体倾斜程度的感受)那么你知道数学上是怎么刻画物体的倾斜程度的吗?今天我们就一起深入学习一下。
探索新知
1.引入探究
以梯子为例,如何比较两个梯子的倾斜程度?
生1:可以看梯子与地面的夹角,也就是梯子的倾斜角,倾斜角大的梯子就陡。
师:这是个好方法,很直接。但是我们知道在生活中有时测量角度会比较困难,有没有其他的方法呢?
生2:角度不行可以用长度嘛,同一个梯子,梯子底端到墙角的距离近,梯子就陡,梯子顶端到墙角的距离远,梯子就陡。
师:非常好,这位同学用到了转化的数学思想方法,同时这也说明了操作方法。那么我们就根据长度尝试一下表示物体的倾斜程度。
2.探究新知
如图,你能比较梯子的倾斜程度吗?
问题1:你准备怎么解决这个问题?小组内讨论1分钟
第一组的共同特征是:梯子顶端到墙角的距离相等。比较梯子底端到墙角的距离就可判断梯子的倾斜程度。
第二组的共同特征是:梯子底端到墙角的距离相等。比较梯子顶端到墙角的距离就可以判断梯子的倾斜程度。
第三组:根据上面两组的探究发现,第三组梯子顶端到墙角的距离不等,梯子底端到墙角的距离也不等。探究出现了困难,需要从已有经验中需找解决办法。将不等转化为相等。
学生活动:学生上台展示解决问题的方法。
对其中一个图形适当地缩放可以实现其中一组量相等。
具体问题一般化,归纳解决问题的方法
问题2:如果是两个一般的图形你可以怎么刻画梯子的倾斜程度呢?
将梯子底端到墙角的距离都化为1
在直角三角形中,倾斜角对边与斜边的比值可以刻画梯子的倾斜程度。成功将角度问题用长度解决了。
归纳总结:
用梯子底端与墙角对的倾斜角,或是顶端到墙角的距离b与梯子底端到墙角的距离a的比值刻画梯子的倾斜程度。
问题3:怎样快速地比较出六个图形中梯子的倾斜程度呢?
方法1:通过测量倾斜角比较。
方法2:把梯子底端到墙角的距离都转化为1,就可以一起快速比较了。
学生活动:学生可以通过一个表格完成
①
②
③
④
⑤
⑥
倾斜角
总结探索结论
倾斜角和都能刻画梯子的倾斜程度,它们是对应的关系,是一种函数关系。
特殊到一般
问题4:你能表示上图斜坡的倾斜程度吗?
缺少直角三角形,需要构造直角三角形,能够构造出很多直角三角形,就会发现这些直角三角形都是相似的,因此得到在直角三角形中倾斜角的对边与邻边的比值只与倾斜角的大小有关。给出正切的概念。
正切的概念
在中,如果锐角A确定,那么∠A的对边与邻边的比便随之确定,这个比叫做∠A的正切,记作tanA,即
总结:倾斜角越大,tanA的值越大,梯子越陡。
给出一个倾斜角就有唯一一个比值tan与它对应,tan是倾斜角的函数,这种刻画三角形边角关系的函数称为三角函数,是倾斜角的正切函数。
同步练习
1.如图,甲乙两个自动扶梯,哪一个自动扶梯比较陡?
2.如图,某人从山脚下的点A走了200m后到达山顶的点B,已知点B到山脚的垂直距离为55m,求山的坡度(结果精确到0.01)
课堂小结
教师的小结
通过本节课的探索学习总结数学思想方法有:转化,特殊到一般,数形结合等。
学生的小结
1.通过本节课的学习在学习方法上你有什么收获?
2.在知识上你有什么收获?
板书设计
三角函数-正切
倾斜角
①
②
③
④
⑤
⑥
倾斜角
倾斜角∠A越大,tanA的值越大,梯子越陡。
教学反思
通过本节课针对本人的教学设计和课堂实施情况进行总结其中处理的特别好的环节有以下几点:1.在探索高度和宽度都不等的两个梯子的倾斜程度的时候,学生的活动时间比较多,充分展示了学生的思维成果,体现了学生的主体作用。2.对于为什么倾斜角的正切值可以表示梯子的倾斜程度,学生在探究的过程中有了自己的理解。3.学生对于三角函数这个抽象的概念也通过函数
的变量对应学生有了清楚的理解。课堂上存在的不足有:学生的对应练习时间有些不足。
通过本节课我的收获有:1.给学生充分表达自己想法的机会,学生会给教师很多的惊喜。2.关注知识的由来和发生过程,学生对知识的理解会更深刻。
