鲁教版(五四制)九上2.1.1 锐角三角函数-正切 教案
文档属性
| 名称 | 鲁教版(五四制)九上2.1.1 锐角三角函数-正切 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 831.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览


文档简介
《锐角三角函数(1)》教学设计
教学目标:
知识与技能:
1、理解正切的概念及意义。
2、了解坡角、坡度的概念,能用正切进行简单的计算。
过程与方法:
1、探索刻画梯子倾斜程度的过程,感受正切与现实生活的联系,体会数形结合的数学思想。
2、通过对正切的学习,逐步学会利用数形结合、从特殊到一般、转化等数学思想,分析问题和解决问题,体会数学在解决实际问题中的应用。
情感态度与价值观:
1、通过探究提高学生对数学的好奇心和求知欲。
2、感受数学来源于生活又应用于生活,理解三角函数与现实生活的联系。
教学重点:
理解锐角正切的概念及意义。
教学难点:
理解为什么正切能够刻画梯子的倾斜程度。
教具准备:
多媒体课件(PPT)
教学方法:
引导—探索法
教学过程:
1、回顾复习
复习:直角三角形中边与边之间的关系、两锐角之间的关系、边与角之间的关系
【设计意图】回顾直角三角形相关知识,为本节课热身。
二、创设情境,导入新课
用多媒体展示生活中与梯子相关的图片,提示生活中使用梯子的时候,有时放得缓有时放得陡,引出如何刻画梯子的倾斜程度。(板书:2.1锐角三角函数—正切)
【设计意图】由学生熟悉的梯子引入新课,紧扣课题,从而自然过渡到下面的探究活动。
三、提出问题,动手实践,探求新知
(一)数学实验
实验工具:课本、直尺
实验过程:用课本做墙壁,尺子当梯子,进行模拟探究,模拟梯子由“缓”变“陡”的过程。
实验思考:
1、梯子在上升变“陡”的过程中,直角三角形中哪些量发生了变化?
2、什么量决定梯子的倾斜程度?
(二)实验结论应用
比较梯子AB和EF哪个更陡
多媒体演示四幅图片
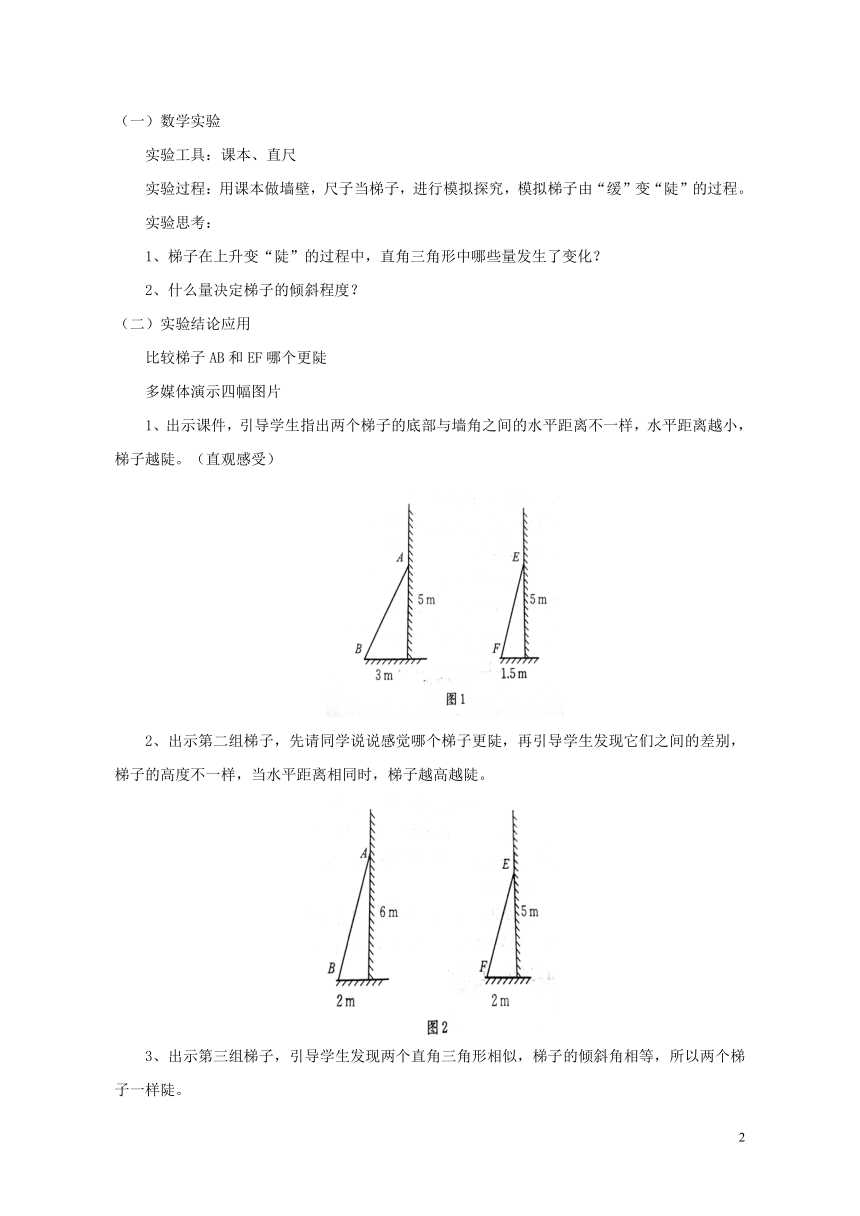
1、出示课件,引导学生指出两个梯子的底部与墙角之间的水平距离不一样,水平距离越小,梯子越陡。(直观感受)
2、出示第二组梯子,先请同学说说感觉哪个梯子更陡,再引导学生发现它们之间的差别,梯子的高度不一样,当水平距离相同时,梯子越高越陡。
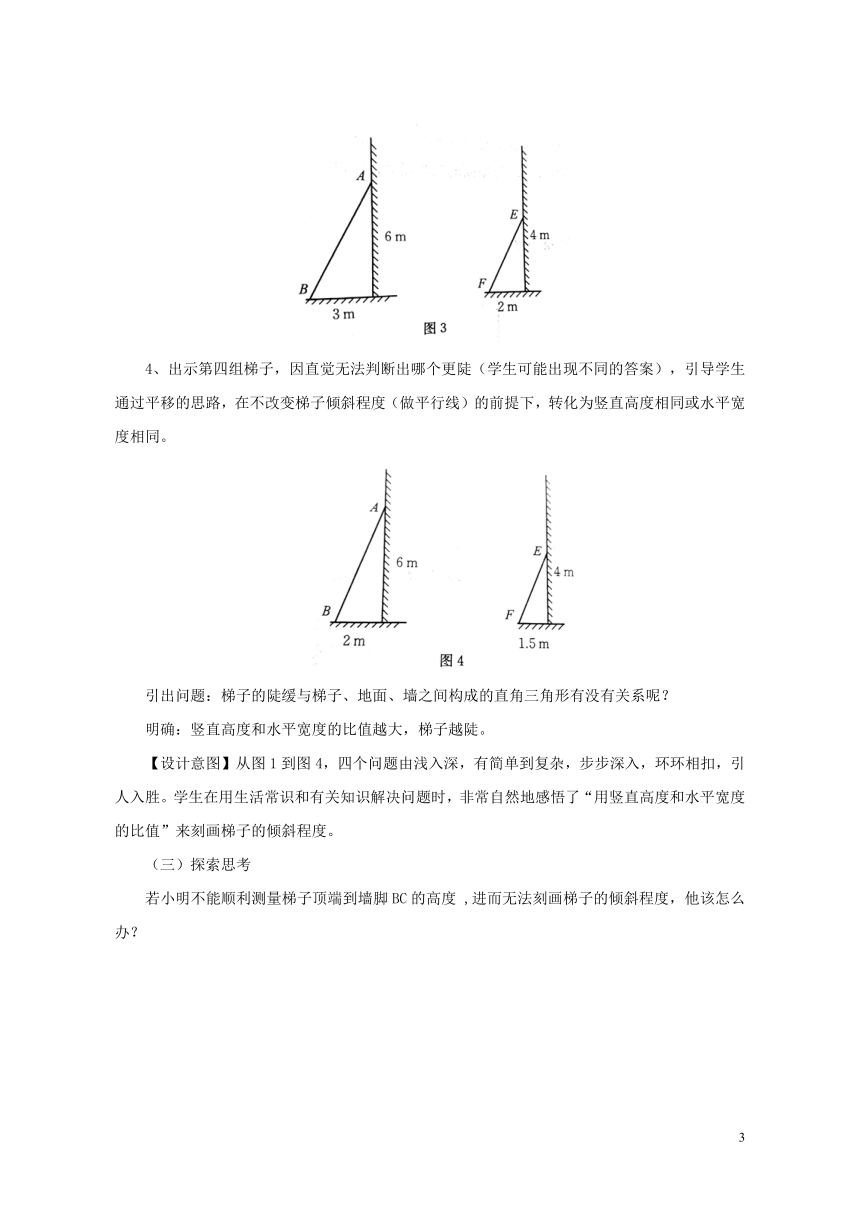
3、出示第三组梯子,引导学生发现两个直角三角形相似,梯子的倾斜角相等,所以两个梯子一样陡。
4、出示第四组梯子,因直觉无法判断出哪个更陡(学生可能出现不同的答案),引导学生通过平移的思路,在不改变梯子倾斜程度(做平行线)的前提下,转化为竖直高度相同或水平宽度相同。
引出问题:梯子的陡缓与梯子、地面、墙之间构成的直角三角形有没有关系呢?
明确:竖直高度和水平宽度的比值越大,梯子越陡。
【设计意图】从图1到图4,四个问题由浅入深,有简单到复杂,步步深入,环环相扣,引人入胜。学生在用生活常识和有关知识解决问题时,非常自然地感悟了“用竖直高度和水平宽度的比值”来刻画梯子的倾斜程度。
(三)探索思考
若小明不能顺利测量梯子顶端到墙脚BC的高度
,进而无法刻画梯子的倾斜程度,他该怎么办?
明确:当梯子的倾斜角一定时,它的竖直高度和水平宽度的比值就一定。
【设计意图】此环节旨在说明当倾斜角确定时,其对边与邻边的比值便随之确定,也就是说,这一比值只与倾斜角有关,而与三角形的大小无关。
(四)构建新知
1、正切的定义:
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比值也随之确定,这个比叫做
∠A的正切,记作tanA。
tanA的值越大,梯子越陡。
2、温馨提示:正切tanA定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的,
∠A是一个锐角.
2)
tanA是一个完整的符号,它表示∠A的正切,记号时习惯省去角的符号“∠”。但角用三个字母表示时如:∠BAC的正切表示为tan∠BAC.
3)
tanA﹥0
没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
【设计意图】理解正切的概念和表示,理解tanA是一个很抽象的符号,它代表一个“比”或“比值”,并理解梯子的倾斜程度与倾斜角的正切之间的关系。
四、跟踪评价
(一)判断真假
1.
如图
(1),tanA=(
)
2.
如图
(2),tanA=(
)
3.
如图
(2),tanB=(
)
4.
如图
(2),tanA=(
)
(二)根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。通过上述计算,你有什么发现?
明确:互余两角的正切值互为倒数
(三)如图,在Rt△ABC中,∠C=90°,AC=12,tanA=2,求BC的值。
(四)下图表示两个自动扶梯,哪一个自动扶梯比较陡?
【设计意图】学生独立完成,合作交流,订正完善,规范步骤。
五、想一想
(一)我们知道,可以用正切刻画梯子的倾斜程度,那么,怎样刻画山坡的倾斜程度呢?
点拨:正切可以描述山坡的坡度
坡面与水平面夹角称为坡角,即坡度等于坡角的正切,坡度越大,坡面越陡
【设计意图】旨在让学生理解坡角和坡度。
(二)跟踪评价
1、如下图,某人从山脚A处走了1000米爬到了山顶B处,该山顶到达的高度h为600米,则该山坡的坡度是
2、河堤横断面如上图所示,堤高BC=5米,迎水坡AB的坡度是
1:
3
,则AC
的长是(
)
A.5米
B.10米
C.15米
D.10米
【设计意图】由学生独立完成,合作交流,订正完善,规范步骤。
6、应用巩固,形成技能
1、如图,
∠BAC位于6×6的方格纸中,则tan∠BAC= .
2、某一建筑物的楼顶是“人”字型,并铺上红瓦装饰。现知道楼顶的坡度超过0.5时,瓦片会滑落下来.请你根据图中数据说明这一楼顶铺设的瓦片是否会滑落下来?
3、如图所示,Rt△ABC是一防洪堤背水坡的横截面图,高度AC的长为12
m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,求增加的宽度BD的长?
【设计意图】通过基本的练习,进一步加强学生对正切和坡度的理解,形成相应的技能
7、课堂小结
引导学生畅所欲言地谈谈本节课的收获。
1、如果锐角A确定,那么∠A的对边与邻边的比值也随之确定,这个比叫做∠A的正切,记作tanA。
2、等角的正切值相等
3、互余两角的正切值互为倒数
4、当锐角α越来越大时,α的正切值也越来越大.
【设计意图】通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
8、课堂检测
1、在Rt△ABC中,∠C=90?,AC=3,AB=5,则
tanB=(
)
A.
B.
C.
D.
2、一拦水坝的坡度为
,若坝高BC=15
米,求坝面
AB的长
九、作业布置
必做:
课本习题2.1
挑战自己:(选做题)
(2008·泰安)直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是多少?
【设计意图】如此布置作业,既巩固知识技能,又减轻学生负担
十、板书设计
二、直角三角形的边角关系
锐角三角函数
∠A的正切,记作tanA
tanA=,tanB=
坡角
坡度
∠A的对边
∠A的邻边
A
B
C
A
B
C
(1)
A
B
7m
10m
(2)
C
B
A
C
3
5
A
4
C
2
B
B
A
C
β
乙
5m
┌
13m
6m
┐
8m
α
甲
A
B
C
A
B
C
┌
A
B
C.
13m
24m
A
B
C
C
B
A
6
8
6
8
C
B
A
E
D
A
C
B
a
b
c
PAGE
2
教学目标:
知识与技能:
1、理解正切的概念及意义。
2、了解坡角、坡度的概念,能用正切进行简单的计算。
过程与方法:
1、探索刻画梯子倾斜程度的过程,感受正切与现实生活的联系,体会数形结合的数学思想。
2、通过对正切的学习,逐步学会利用数形结合、从特殊到一般、转化等数学思想,分析问题和解决问题,体会数学在解决实际问题中的应用。
情感态度与价值观:
1、通过探究提高学生对数学的好奇心和求知欲。
2、感受数学来源于生活又应用于生活,理解三角函数与现实生活的联系。
教学重点:
理解锐角正切的概念及意义。
教学难点:
理解为什么正切能够刻画梯子的倾斜程度。
教具准备:
多媒体课件(PPT)
教学方法:
引导—探索法
教学过程:
1、回顾复习
复习:直角三角形中边与边之间的关系、两锐角之间的关系、边与角之间的关系
【设计意图】回顾直角三角形相关知识,为本节课热身。
二、创设情境,导入新课
用多媒体展示生活中与梯子相关的图片,提示生活中使用梯子的时候,有时放得缓有时放得陡,引出如何刻画梯子的倾斜程度。(板书:2.1锐角三角函数—正切)
【设计意图】由学生熟悉的梯子引入新课,紧扣课题,从而自然过渡到下面的探究活动。
三、提出问题,动手实践,探求新知
(一)数学实验
实验工具:课本、直尺
实验过程:用课本做墙壁,尺子当梯子,进行模拟探究,模拟梯子由“缓”变“陡”的过程。
实验思考:
1、梯子在上升变“陡”的过程中,直角三角形中哪些量发生了变化?
2、什么量决定梯子的倾斜程度?
(二)实验结论应用
比较梯子AB和EF哪个更陡
多媒体演示四幅图片
1、出示课件,引导学生指出两个梯子的底部与墙角之间的水平距离不一样,水平距离越小,梯子越陡。(直观感受)
2、出示第二组梯子,先请同学说说感觉哪个梯子更陡,再引导学生发现它们之间的差别,梯子的高度不一样,当水平距离相同时,梯子越高越陡。
3、出示第三组梯子,引导学生发现两个直角三角形相似,梯子的倾斜角相等,所以两个梯子一样陡。
4、出示第四组梯子,因直觉无法判断出哪个更陡(学生可能出现不同的答案),引导学生通过平移的思路,在不改变梯子倾斜程度(做平行线)的前提下,转化为竖直高度相同或水平宽度相同。
引出问题:梯子的陡缓与梯子、地面、墙之间构成的直角三角形有没有关系呢?
明确:竖直高度和水平宽度的比值越大,梯子越陡。
【设计意图】从图1到图4,四个问题由浅入深,有简单到复杂,步步深入,环环相扣,引人入胜。学生在用生活常识和有关知识解决问题时,非常自然地感悟了“用竖直高度和水平宽度的比值”来刻画梯子的倾斜程度。
(三)探索思考
若小明不能顺利测量梯子顶端到墙脚BC的高度
,进而无法刻画梯子的倾斜程度,他该怎么办?
明确:当梯子的倾斜角一定时,它的竖直高度和水平宽度的比值就一定。
【设计意图】此环节旨在说明当倾斜角确定时,其对边与邻边的比值便随之确定,也就是说,这一比值只与倾斜角有关,而与三角形的大小无关。
(四)构建新知
1、正切的定义:
在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻边的比值也随之确定,这个比叫做
∠A的正切,记作tanA。
tanA的值越大,梯子越陡。
2、温馨提示:正切tanA定义的几点说明:
1)初中阶段,正切是在直角三角形中定义的,
∠A是一个锐角.
2)
tanA是一个完整的符号,它表示∠A的正切,记号时习惯省去角的符号“∠”。但角用三个字母表示时如:∠BAC的正切表示为tan∠BAC.
3)
tanA﹥0
没有单位,它表示一个比值,即直角三角形中锐角∠A的对边与邻边的比(注意顺序).
4)
tanA的大小只与∠A的大小有关,而与直角三角形的边长无关。
【设计意图】理解正切的概念和表示,理解tanA是一个很抽象的符号,它代表一个“比”或“比值”,并理解梯子的倾斜程度与倾斜角的正切之间的关系。
四、跟踪评价
(一)判断真假
1.
如图
(1),tanA=(
)
2.
如图
(2),tanA=(
)
3.
如图
(2),tanB=(
)
4.
如图
(2),tanA=(
)
(二)根据下列图中所给条件分别求出下列图中∠A、∠B的正切值。通过上述计算,你有什么发现?
明确:互余两角的正切值互为倒数
(三)如图,在Rt△ABC中,∠C=90°,AC=12,tanA=2,求BC的值。
(四)下图表示两个自动扶梯,哪一个自动扶梯比较陡?
【设计意图】学生独立完成,合作交流,订正完善,规范步骤。
五、想一想
(一)我们知道,可以用正切刻画梯子的倾斜程度,那么,怎样刻画山坡的倾斜程度呢?
点拨:正切可以描述山坡的坡度
坡面与水平面夹角称为坡角,即坡度等于坡角的正切,坡度越大,坡面越陡
【设计意图】旨在让学生理解坡角和坡度。
(二)跟踪评价
1、如下图,某人从山脚A处走了1000米爬到了山顶B处,该山顶到达的高度h为600米,则该山坡的坡度是
2、河堤横断面如上图所示,堤高BC=5米,迎水坡AB的坡度是
1:
3
,则AC
的长是(
)
A.5米
B.10米
C.15米
D.10米
【设计意图】由学生独立完成,合作交流,订正完善,规范步骤。
6、应用巩固,形成技能
1、如图,
∠BAC位于6×6的方格纸中,则tan∠BAC= .
2、某一建筑物的楼顶是“人”字型,并铺上红瓦装饰。现知道楼顶的坡度超过0.5时,瓦片会滑落下来.请你根据图中数据说明这一楼顶铺设的瓦片是否会滑落下来?
3、如图所示,Rt△ABC是一防洪堤背水坡的横截面图,高度AC的长为12
m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡比为1:1.5的斜坡AD,求增加的宽度BD的长?
【设计意图】通过基本的练习,进一步加强学生对正切和坡度的理解,形成相应的技能
7、课堂小结
引导学生畅所欲言地谈谈本节课的收获。
1、如果锐角A确定,那么∠A的对边与邻边的比值也随之确定,这个比叫做∠A的正切,记作tanA。
2、等角的正切值相等
3、互余两角的正切值互为倒数
4、当锐角α越来越大时,α的正切值也越来越大.
【设计意图】通过小结,回顾探索新知识的过程,进一步感悟其中蕴含的数学思想方法,提高学生的概括能力,培养学生良好的回顾和反思的习惯。
8、课堂检测
1、在Rt△ABC中,∠C=90?,AC=3,AB=5,则
tanB=(
)
A.
B.
C.
D.
2、一拦水坝的坡度为
,若坝高BC=15
米,求坝面
AB的长
九、作业布置
必做:
课本习题2.1
挑战自己:(选做题)
(2008·泰安)直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是多少?
【设计意图】如此布置作业,既巩固知识技能,又减轻学生负担
十、板书设计
二、直角三角形的边角关系
锐角三角函数
∠A的正切,记作tanA
tanA=,tanB=
坡角
坡度
∠A的对边
∠A的邻边
A
B
C
A
B
C
(1)
A
B
7m
10m
(2)
C
B
A
C
3
5
A
4
C
2
B
B
A
C
β
乙
5m
┌
13m
6m
┐
8m
α
甲
A
B
C
A
B
C
┌
A
B
C.
13m
24m
A
B
C
C
B
A
6
8
6
8
C
B
A
E
D
A
C
B
a
b
c
PAGE
2
