鲁教版(五四制)九上2.3用计算器求锐角三角函数值 教案
文档属性
| 名称 | 鲁教版(五四制)九上2.3用计算器求锐角三角函数值 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 392.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 00:00:00 | ||
图片预览

文档简介
2.3
用计算器求锐角的三角函数值
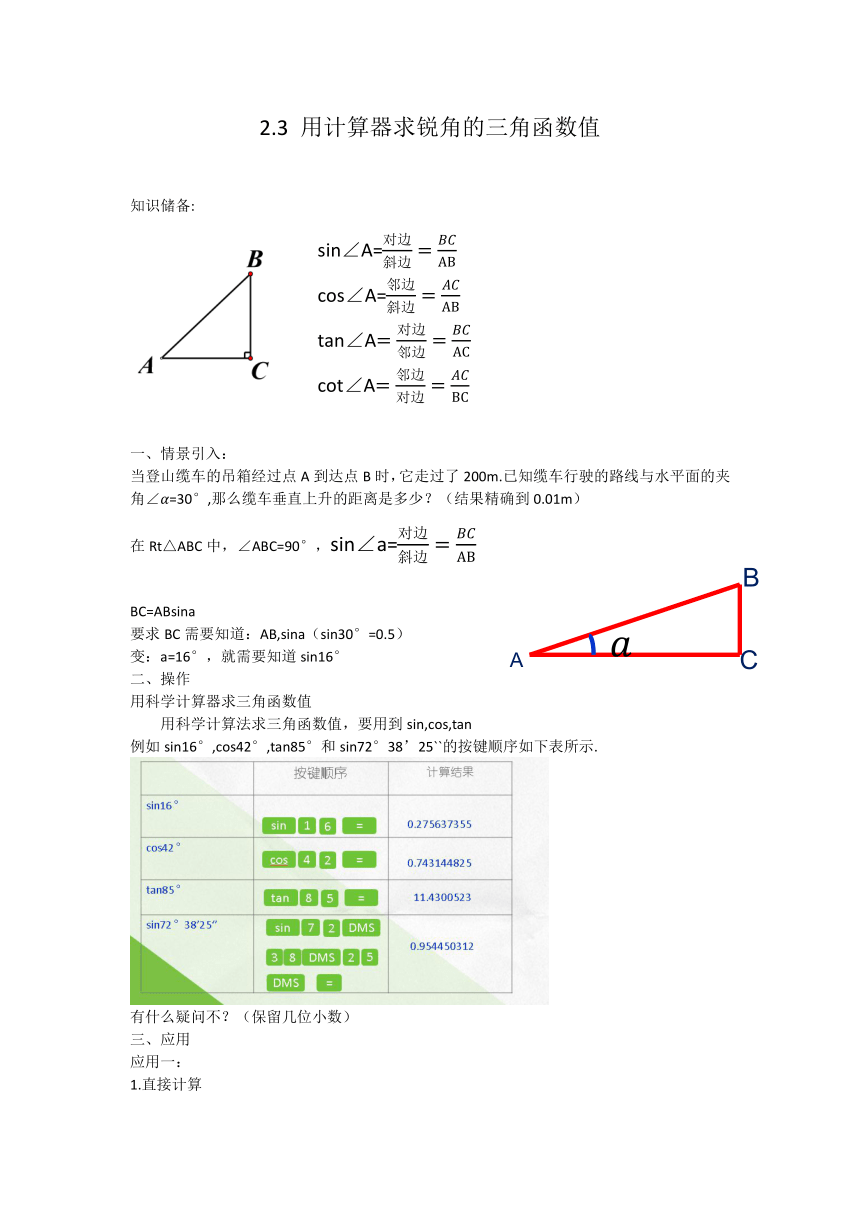
知识储备:
一、情景引入:
当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角∠?=30°,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
在Rt△ABC中,∠ABC=90°,sin∠a=
BC=ABsina
要求BC需要知道:AB,sina(sin30°=0.5)
变:a=16°,就需要知道sin16°
二、操作
用科学计算器求三角函数值
用科学计算法求三角函数值,要用到sin,cos,tan
例如sin16°,cos42°,tan85°和sin72°38’25``的按键顺序如下表所示.
有什么疑问不?(保留几位小数)
三、应用
应用一:
1.直接计算
(1)sin32°(2)cos24.53°(3)sin62°11’(4)cos51°42’20’’(5)tan39°39’39’’
2.加减
(1)sin56°+
cos61°+
tan76°(2)sin35°-3tan25°
3.乘除
计算技巧:
1.按键顺序
2.乘除不是单个三角函数值要加括号
3.按照题目要求保留小数
应用二:探索规律
用计算器求出下列三角函数的值,并填入下表
讨论找出规律:
1.随着a的度数增大,正弦值逐渐增大,
正切值逐渐增大,而余弦值逐渐减少
2.sina=cos(90°-a)
3.tana
=????/????
应用三:解决实际问题
一个人由山底爬到山顶,需要先爬40°的山坡
300m,再爬30°的山坡100m,求山高.(结果精确到0.1m)
变式1:
一楼门前的台阶高出地面1.2m,计划拆除台阶,改建成可供轮椅行走的斜坡,根据这个城市的规定,供轮椅行走的斜坡倾斜角不得超过9°,从斜坡的起点至楼门的最短水平距离是多少?(结果精确到0.1m)
变式2:
一座厂房屋顶人字架的跨度为10m,上弦AB=BD,∠A=26°,求中柱BC和上弦AB的长(结果精确到0.1m)
归纳总结:
三种类型:
类型:知道锐角与斜边求对边
知道锐角与对边求邻边
知道锐角与邻边求对边和斜边
解题思路:
1.找准条件并建造数学模型(画图)
2.分析已知和未知
选择所用公式
3.根据公式利用计算器求值
四、对标自查:
1.本节课达标了
吗?
2.还有没解决的问题吗?
3.积极发言了吗?
达标检测
1.用计算器计算
(1)sin23°5`+cos66°55`
(2)cos14°28`-tan42°57`
2.为了测量一条河流的宽度,一位测量员在和备案东西方向相距180m的PQ两点分别测定对岸河边的一棵树T的位置,T在P的正南方向,在Q的南偏西50°的方向,求河宽PT(结果精确到1m)
自我评价:
小组评价:
教师评价:
用计算器求锐角的三角函数值
知识储备:
一、情景引入:
当登山缆车的吊箱经过点A到达点B时,它走过了200m.已知缆车行驶的路线与水平面的夹角∠?=30°,那么缆车垂直上升的距离是多少?(结果精确到0.01m)
在Rt△ABC中,∠ABC=90°,sin∠a=
BC=ABsina
要求BC需要知道:AB,sina(sin30°=0.5)
变:a=16°,就需要知道sin16°
二、操作
用科学计算器求三角函数值
用科学计算法求三角函数值,要用到sin,cos,tan
例如sin16°,cos42°,tan85°和sin72°38’25``的按键顺序如下表所示.
有什么疑问不?(保留几位小数)
三、应用
应用一:
1.直接计算
(1)sin32°(2)cos24.53°(3)sin62°11’(4)cos51°42’20’’(5)tan39°39’39’’
2.加减
(1)sin56°+
cos61°+
tan76°(2)sin35°-3tan25°
3.乘除
计算技巧:
1.按键顺序
2.乘除不是单个三角函数值要加括号
3.按照题目要求保留小数
应用二:探索规律
用计算器求出下列三角函数的值,并填入下表
讨论找出规律:
1.随着a的度数增大,正弦值逐渐增大,
正切值逐渐增大,而余弦值逐渐减少
2.sina=cos(90°-a)
3.tana
=????/????
应用三:解决实际问题
一个人由山底爬到山顶,需要先爬40°的山坡
300m,再爬30°的山坡100m,求山高.(结果精确到0.1m)
变式1:
一楼门前的台阶高出地面1.2m,计划拆除台阶,改建成可供轮椅行走的斜坡,根据这个城市的规定,供轮椅行走的斜坡倾斜角不得超过9°,从斜坡的起点至楼门的最短水平距离是多少?(结果精确到0.1m)
变式2:
一座厂房屋顶人字架的跨度为10m,上弦AB=BD,∠A=26°,求中柱BC和上弦AB的长(结果精确到0.1m)
归纳总结:
三种类型:
类型:知道锐角与斜边求对边
知道锐角与对边求邻边
知道锐角与邻边求对边和斜边
解题思路:
1.找准条件并建造数学模型(画图)
2.分析已知和未知
选择所用公式
3.根据公式利用计算器求值
四、对标自查:
1.本节课达标了
吗?
2.还有没解决的问题吗?
3.积极发言了吗?
达标检测
1.用计算器计算
(1)sin23°5`+cos66°55`
(2)cos14°28`-tan42°57`
2.为了测量一条河流的宽度,一位测量员在和备案东西方向相距180m的PQ两点分别测定对岸河边的一棵树T的位置,T在P的正南方向,在Q的南偏西50°的方向,求河宽PT(结果精确到1m)
自我评价:
小组评价:
教师评价:
