鲁教版(五四制)九上1.3 反比例函数的应用 教案
文档属性
| 名称 | 鲁教版(五四制)九上1.3 反比例函数的应用 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 15:57:24 | ||
图片预览


文档简介
九年级上册《1.3反比例函数的应用》教学设计
【设计理念】
借用《乘风破浪》的歌词,交代本节课学习内容。通过“创境激思”,激发数学思考,让学生在思考中得以提升。经历“温故知新”、“新知探究”,“总结提升”方法与思想。利用“跟踪训练”、“训练提升”、培养学生多方法、多角度思考问题的能力,感受学习变量间关系的必要性,体会函数的模型思想,进一步发展符号意识。通过一系列“变式训练”,层层加深,让学生在思考中成长,培养学生迎难而上、契而不舍的科学精神。最后再次借用《乘风破浪》的歌词“扬心潮澎湃的帆”,“驾乘风破浪的船”祝愿学生在求学路上奋勇向前。
【教学目标】
(1)
知识与技能目标
1、能根据实际问题中的条件确定反比例函数的解析式,并能根据图像条件指出函数值随自变量变化情况。
2、能将实际问题转化成反比例函数模型。
3、综合运用一次函数和反比例函数的知识解决有关问题。
(二)过程与方法目标
1、经历“实际问题—数学模型—解决问题”的过程,体会“数学是现实的”,发展分析问题、解决问题的能力,增强应用意识。
2、通过培养学生看图像、识图像、读图像的能力,体会用“数、形”结合思想解答函数问题。
3、通过对问题用不同方法,从不同角度的思考、分析过程,渗透一题多解的方法,培养学生的思维灵活性。
(三)情感与态度价值观目标
1、调动学生参与数学活动的积极性,体验数学活动充满着探索性和创造性。
2、让学生经历分析实际问题中的两个变量之间的关系,并解决有关问题的过程,发展应用意识,
提高实践能力,感悟数学来源于生活实践、服务于生产实践的理性精神。
3、发展学生从图象中获取信息的能力,渗透数形结合的思想方法,通过对实际问题的分析与解决,让学生体验数学的价值,培养学生对数学的兴趣。
【教学重点】
将实际问题抽象为数学问题,建立反比例函数模型,并能用反比例函数的性质去解决实际问题。
【教学难点】
根据实际问题的条件确定反比例函数的表达式,及反比例函数与其它知识的综合运用。
【教学资源】PPT课件,课宝软件,Mp4歌曲《乘风破浪》
【教学过程及设计意图】
1、创境激思
学校生物小组要进行湿地植物调查,需横跨一片十几米宽的烂泥湿地。为了安全迅速通过湿地,他们要沿着前进路线铺垫若干木板,构筑一条临时通道,才能顺利完成了任务。
师:问题1:
你能解释他们这样做的道理吗?
生:主要是为减小压强而安全通过。
师:问题2:当人和木板对湿地的压力一定时,随着木板面积S(m2)
变化,人和木板对地面的压强P(Pa)将如何变化?
生:由P=
可知,当压力一定时,随着木板面积的增大,
人和木板对地面的压强减小。
【把原题的“野外考察小组”改成“生物小组”,将课本知识背景步入学生实际学习生活。结合学校“生物小组”植物调查活动的开展,以帮助同学获取“木板”为主线做自然铺垫。】
2、温故知新
师:感叹生物小组同学们物理知识运用的恰到好处,可现在,他们却因没有木板而发愁。请同学们开动脑筋带动双手,从老师这儿获取更多的木板,以解他们的燃眉之急。
请同学们选择你喜欢的颜色木板。
【分别由学生讲解,其他学生评价,老师再进行梳理和强调反比例函数知识的基本知识与技能,为下一步实际问题的解决做好充分准备。】
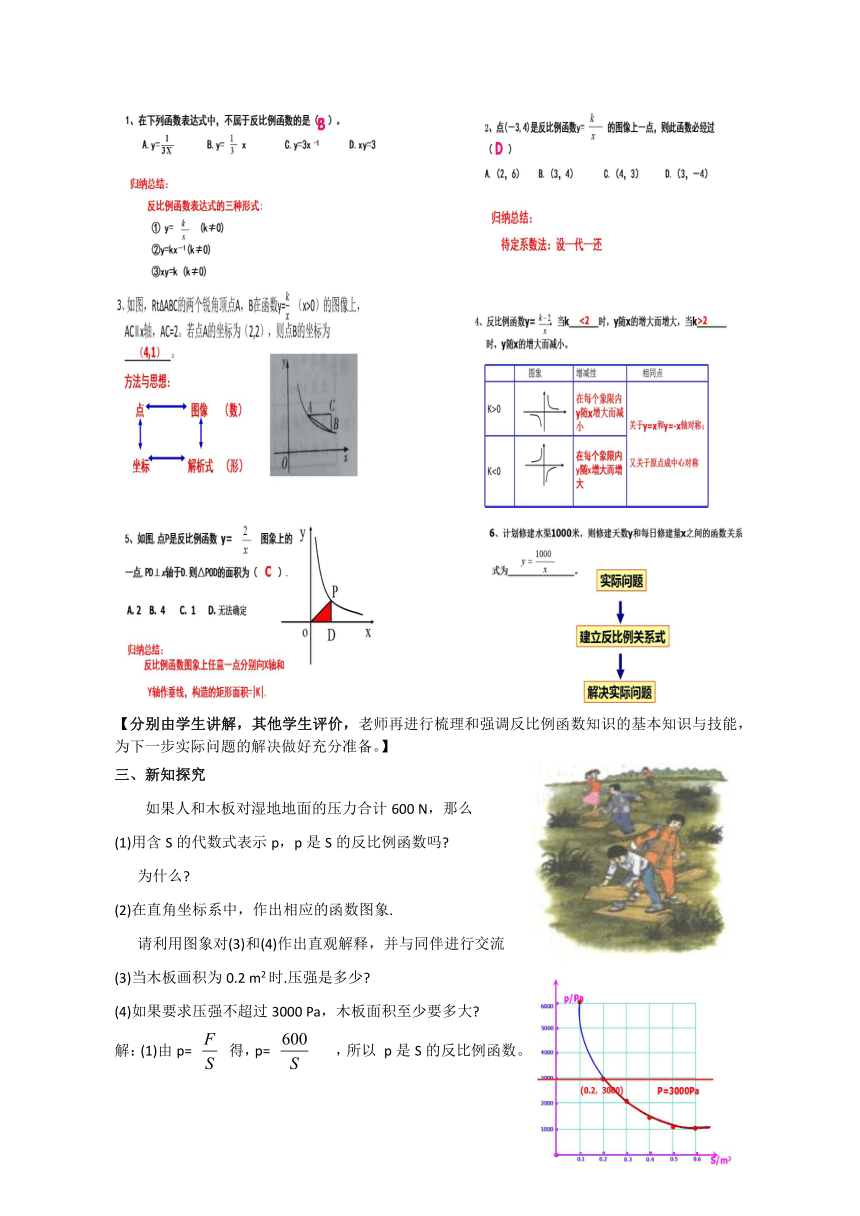
3、新知探究
如果人和木板对湿地地面的压力合计600
N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗?
为什么?
(2)在直角坐标系中,作出相应的函数图象.
请利用图象对(3)和(4)作出直观解释,并与同伴进行交流
(3)当木板画积为0.2
m2时.压强是多少?
(4)如果要求压强不超过3000
Pa,木板面积至少要多大?
解:(1)由p=
得,p=
,所以
p是S的反比例函数。
(3)当p=3000
Pa时,S=
=0.2(m2).
(4)第一种:在图像上过(0.2,3000)做y轴垂线,该点和该
点一下部分的曲线是压强不超过3000Pa,因此木板面积至少得0.2m2。
第二种:当p≥3000,由p=
,
得≥3000
S≤0.2
答:木板面积至少得0.2m2。
【调整原来问题的顺序,强调让学生先画图,改变习惯用代数方法来解决问题的方法。让学生齐声朗读试题,一是帮助学生加深题干印象,二是帮助学生提高瞬间思考效率。通过学生自主探究、师友交流、上台展示等方式,培养学生看图像、识图像、读图像的能力,自然运用“数、形”结合思想解答函数问题。利用课宝软件,及时将学生完成情况图片上传,节省时间,而且使得同一问题的不同方法能在同一时间对比展示,达到更方便、更快捷、更直观的拓展了学生的思维角度的目的。最后,通过PPT课件与学生共同回忆利用图像解决函数问题的过程,强调数形结合的思想,领会实际问题的数学意义,体会数形统一。】
师:总结提升
四、跟踪训练
蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示,
请结合图像回答问题:
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
【让学生齐声朗读试题,并限定时间完成试题。通过黑板上学生试题解答过程,规范所有学生反比例函数解题步骤。再通过课宝软件拍照,利用图像方法,学生教学生的加强数形结合思想的运用,增强应用意识。】
五、训练提升(一)
为迎接2018年青岛“上合峰会”的召开,某工艺品厂每天要生产一种精美工艺品60个,若每名工人一天能够做该工艺品x个,则需工人y名。
(1)求y关于x的函数解析式;
(2)若一名工人每天能做的工艺品个数最少6个,最多8个,估计该工艺品厂每天需要这种工艺品的工人的人数范围。
【限定时间完成试题。发现学生问题点,在学生辩疑中,帮助他们解决问题(2)当x=6时,求得y=7.5,而需要的工人数取正整数,因此y=8,工人的人数范围是8≤y≤10人。另外,可利用课宝软件画图,直观说明反比例函数图像上符合条件的范围。】
五、训练提升(二)
如图所示,正比例函数y=k1x的图象与反比例
函数
y=
的图象交
于A、B两点,其中点A的坐标为().
(1)分别写出这两个函数的表达式.
(2)你能求出点B的坐标吗?你是怎样求的?
【利用已有的正比例、反比例函数的知识经验,得到问题(1)答案。对于问题(2),根据学生情况,利用课宝软件将两种方法拍照,形成直观的对比,根据“若两函数有交点,则函数值相等”的代数法,列方程求得B点坐标,根据“正比例函数和反比例函数都是关于点O的中心对称图形”,直接得到点A与点B关于点O中心对称,求得B点坐标。通过第二种方法,再次巩固数形结合思想方法,并体验数学的对称美。通过对问题用不同方法,从不同角度的思考、分析过程,渗透一题多解的方法,培养学生的思维灵活性】
六、变式训练(一)
如图所示,正比例函数y=
的图象与反比例
函数y=
的图象交于A、B两点,过点A做
AM⊥X轴,过点B做BM⊥Y轴,交于点M。若⊿ABM
的面积等于12,则=_________
【结合“若正比例函数与反比例函数相交于不同象限两交点,则两交点关于原点中心对称。”、“反比例函数图象上任意一点分别向X轴和
Y轴作垂线,构造的矩形面积=|K|。”和相似三角形的性质,用不同的方法分析。让学生充分展示思维,激起共鸣,巩固数形结合思想】
六、变式训练(二)
如图,反比例函数y=
与一次函数
y=
的图像,
交于A、B两点。求(1)A、B点坐标。(2)求⊿AOB的面积。
【可作为课后思考题,考察学生对图形分解与整合的能力,在探索中学会反思,挑战学生能力,坚定学习数学的信心。】
师:让我们再一次聆听《乘风破浪》,借歌词“扬心潮澎湃的帆,驾乘风波浪的船”,祝愿同学们在求学路上勇往直前。谢谢!
七、作业布置
必做:P16习题1.4
1、2
选作:P16联系拓展
实践作业:利用废弃纸板,结合数学图形,设计环保标志。
【课后作业分层布置,尊重学生个体差异,让不同层次的学生所能收获喜悦。另外,回归开头的问题情境,回收“木板”,变废为宝,增强学生的环保意识,进行美育教育。】
【设计理念】
借用《乘风破浪》的歌词,交代本节课学习内容。通过“创境激思”,激发数学思考,让学生在思考中得以提升。经历“温故知新”、“新知探究”,“总结提升”方法与思想。利用“跟踪训练”、“训练提升”、培养学生多方法、多角度思考问题的能力,感受学习变量间关系的必要性,体会函数的模型思想,进一步发展符号意识。通过一系列“变式训练”,层层加深,让学生在思考中成长,培养学生迎难而上、契而不舍的科学精神。最后再次借用《乘风破浪》的歌词“扬心潮澎湃的帆”,“驾乘风破浪的船”祝愿学生在求学路上奋勇向前。
【教学目标】
(1)
知识与技能目标
1、能根据实际问题中的条件确定反比例函数的解析式,并能根据图像条件指出函数值随自变量变化情况。
2、能将实际问题转化成反比例函数模型。
3、综合运用一次函数和反比例函数的知识解决有关问题。
(二)过程与方法目标
1、经历“实际问题—数学模型—解决问题”的过程,体会“数学是现实的”,发展分析问题、解决问题的能力,增强应用意识。
2、通过培养学生看图像、识图像、读图像的能力,体会用“数、形”结合思想解答函数问题。
3、通过对问题用不同方法,从不同角度的思考、分析过程,渗透一题多解的方法,培养学生的思维灵活性。
(三)情感与态度价值观目标
1、调动学生参与数学活动的积极性,体验数学活动充满着探索性和创造性。
2、让学生经历分析实际问题中的两个变量之间的关系,并解决有关问题的过程,发展应用意识,
提高实践能力,感悟数学来源于生活实践、服务于生产实践的理性精神。
3、发展学生从图象中获取信息的能力,渗透数形结合的思想方法,通过对实际问题的分析与解决,让学生体验数学的价值,培养学生对数学的兴趣。
【教学重点】
将实际问题抽象为数学问题,建立反比例函数模型,并能用反比例函数的性质去解决实际问题。
【教学难点】
根据实际问题的条件确定反比例函数的表达式,及反比例函数与其它知识的综合运用。
【教学资源】PPT课件,课宝软件,Mp4歌曲《乘风破浪》
【教学过程及设计意图】
1、创境激思
学校生物小组要进行湿地植物调查,需横跨一片十几米宽的烂泥湿地。为了安全迅速通过湿地,他们要沿着前进路线铺垫若干木板,构筑一条临时通道,才能顺利完成了任务。
师:问题1:
你能解释他们这样做的道理吗?
生:主要是为减小压强而安全通过。
师:问题2:当人和木板对湿地的压力一定时,随着木板面积S(m2)
变化,人和木板对地面的压强P(Pa)将如何变化?
生:由P=
可知,当压力一定时,随着木板面积的增大,
人和木板对地面的压强减小。
【把原题的“野外考察小组”改成“生物小组”,将课本知识背景步入学生实际学习生活。结合学校“生物小组”植物调查活动的开展,以帮助同学获取“木板”为主线做自然铺垫。】
2、温故知新
师:感叹生物小组同学们物理知识运用的恰到好处,可现在,他们却因没有木板而发愁。请同学们开动脑筋带动双手,从老师这儿获取更多的木板,以解他们的燃眉之急。
请同学们选择你喜欢的颜色木板。
【分别由学生讲解,其他学生评价,老师再进行梳理和强调反比例函数知识的基本知识与技能,为下一步实际问题的解决做好充分准备。】
3、新知探究
如果人和木板对湿地地面的压力合计600
N,那么
(1)用含S的代数式表示p,p是S的反比例函数吗?
为什么?
(2)在直角坐标系中,作出相应的函数图象.
请利用图象对(3)和(4)作出直观解释,并与同伴进行交流
(3)当木板画积为0.2
m2时.压强是多少?
(4)如果要求压强不超过3000
Pa,木板面积至少要多大?
解:(1)由p=
得,p=
,所以
p是S的反比例函数。
(3)当p=3000
Pa时,S=
=0.2(m2).
(4)第一种:在图像上过(0.2,3000)做y轴垂线,该点和该
点一下部分的曲线是压强不超过3000Pa,因此木板面积至少得0.2m2。
第二种:当p≥3000,由p=
,
得≥3000
S≤0.2
答:木板面积至少得0.2m2。
【调整原来问题的顺序,强调让学生先画图,改变习惯用代数方法来解决问题的方法。让学生齐声朗读试题,一是帮助学生加深题干印象,二是帮助学生提高瞬间思考效率。通过学生自主探究、师友交流、上台展示等方式,培养学生看图像、识图像、读图像的能力,自然运用“数、形”结合思想解答函数问题。利用课宝软件,及时将学生完成情况图片上传,节省时间,而且使得同一问题的不同方法能在同一时间对比展示,达到更方便、更快捷、更直观的拓展了学生的思维角度的目的。最后,通过PPT课件与学生共同回忆利用图像解决函数问题的过程,强调数形结合的思想,领会实际问题的数学意义,体会数形统一。】
师:总结提升
四、跟踪训练
蓄电池的电压为定值.使用此电源时,电流I(A)与电阻R(Ω)之间的函数关系如图所示,
请结合图像回答问题:
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
(2)如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
【让学生齐声朗读试题,并限定时间完成试题。通过黑板上学生试题解答过程,规范所有学生反比例函数解题步骤。再通过课宝软件拍照,利用图像方法,学生教学生的加强数形结合思想的运用,增强应用意识。】
五、训练提升(一)
为迎接2018年青岛“上合峰会”的召开,某工艺品厂每天要生产一种精美工艺品60个,若每名工人一天能够做该工艺品x个,则需工人y名。
(1)求y关于x的函数解析式;
(2)若一名工人每天能做的工艺品个数最少6个,最多8个,估计该工艺品厂每天需要这种工艺品的工人的人数范围。
【限定时间完成试题。发现学生问题点,在学生辩疑中,帮助他们解决问题(2)当x=6时,求得y=7.5,而需要的工人数取正整数,因此y=8,工人的人数范围是8≤y≤10人。另外,可利用课宝软件画图,直观说明反比例函数图像上符合条件的范围。】
五、训练提升(二)
如图所示,正比例函数y=k1x的图象与反比例
函数
y=
的图象交
于A、B两点,其中点A的坐标为().
(1)分别写出这两个函数的表达式.
(2)你能求出点B的坐标吗?你是怎样求的?
【利用已有的正比例、反比例函数的知识经验,得到问题(1)答案。对于问题(2),根据学生情况,利用课宝软件将两种方法拍照,形成直观的对比,根据“若两函数有交点,则函数值相等”的代数法,列方程求得B点坐标,根据“正比例函数和反比例函数都是关于点O的中心对称图形”,直接得到点A与点B关于点O中心对称,求得B点坐标。通过第二种方法,再次巩固数形结合思想方法,并体验数学的对称美。通过对问题用不同方法,从不同角度的思考、分析过程,渗透一题多解的方法,培养学生的思维灵活性】
六、变式训练(一)
如图所示,正比例函数y=
的图象与反比例
函数y=
的图象交于A、B两点,过点A做
AM⊥X轴,过点B做BM⊥Y轴,交于点M。若⊿ABM
的面积等于12,则=_________
【结合“若正比例函数与反比例函数相交于不同象限两交点,则两交点关于原点中心对称。”、“反比例函数图象上任意一点分别向X轴和
Y轴作垂线,构造的矩形面积=|K|。”和相似三角形的性质,用不同的方法分析。让学生充分展示思维,激起共鸣,巩固数形结合思想】
六、变式训练(二)
如图,反比例函数y=
与一次函数
y=
的图像,
交于A、B两点。求(1)A、B点坐标。(2)求⊿AOB的面积。
【可作为课后思考题,考察学生对图形分解与整合的能力,在探索中学会反思,挑战学生能力,坚定学习数学的信心。】
师:让我们再一次聆听《乘风破浪》,借歌词“扬心潮澎湃的帆,驾乘风波浪的船”,祝愿同学们在求学路上勇往直前。谢谢!
七、作业布置
必做:P16习题1.4
1、2
选作:P16联系拓展
实践作业:利用废弃纸板,结合数学图形,设计环保标志。
【课后作业分层布置,尊重学生个体差异,让不同层次的学生所能收获喜悦。另外,回归开头的问题情境,回收“木板”,变废为宝,增强学生的环保意识,进行美育教育。】
