八年级数学利用频率估计概率
图片预览








文档简介
(共34张PPT)
请拿出你的导学案,课本,双色笔,典型题本还有你的激情、动力和目标
全力投入会使你与众不同
你是最优秀的,你一定能做的更好!
温馨提示
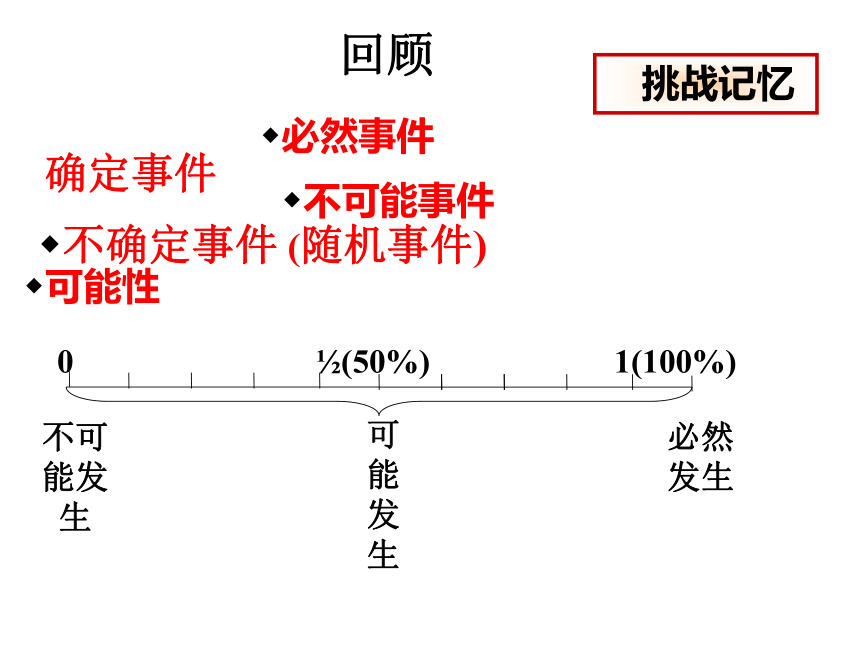
必然事件
不可能事件
可能性
0 (50%) 1(100%)
不可能发生
可能发生
必然发生
不确定事件 (随机事件)
回顾
挑战记忆
确定事件
概率 事件发生的可能性,也称为事件发生的概率.
必然事件发生的概率为1(或100%),
记作P(必然事件)=1;
不可能事件发生的概率为0,
记作P(不可能事件)=0;
随机事件(不确定事件)发生的概率介于0~1之 间,即0如果A为随机事件(不确定事件),
那么0挑战记忆
m为事件A可能发生的结果数
n为所有等可能结果的总数
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
频数:每个对象出现的次数
频率:每个对象出现的次数 与总次数
的比值
问题1.掷一枚硬币,落地后会出现几种结果?
。正面向上、反面向上,2种可能性相等
问题2.掷两枚硬币(硬币A,硬币B),落地后会出现几种结果?
。A正B正,A正B反,A反B正,A反B反,四种可能性相等。
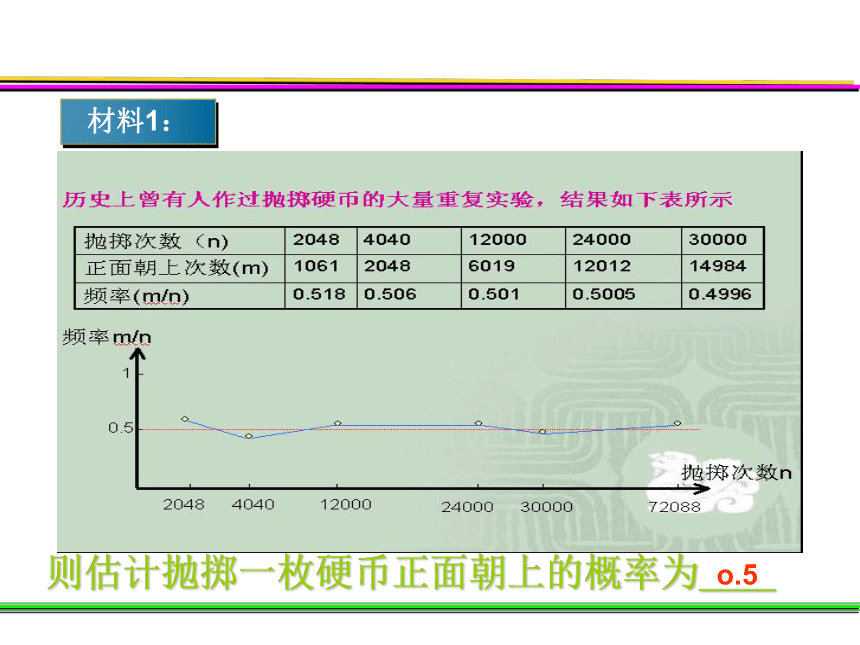
材料1:
则估计抛掷一枚硬币正面朝上的概率为__
o.5
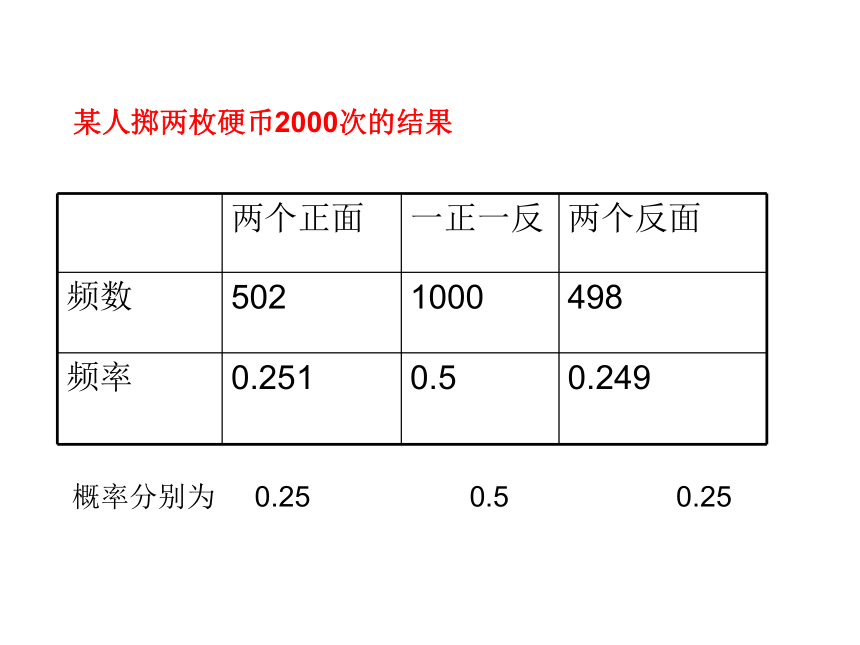
两个正面 一正一反 两个反面
频数 502 1000 498
频率 0.251 0.5 0.249
某人掷两枚硬币2000次的结果
概率分别为 0.25 0.5 0.25
在进行大量重复试验时,随着实验次数的增加,
一个不确定事件发生的频率会逐渐稳定到某一个数值。
我们可以用平稳时的频率来估计这个事件发生的概率.
结论
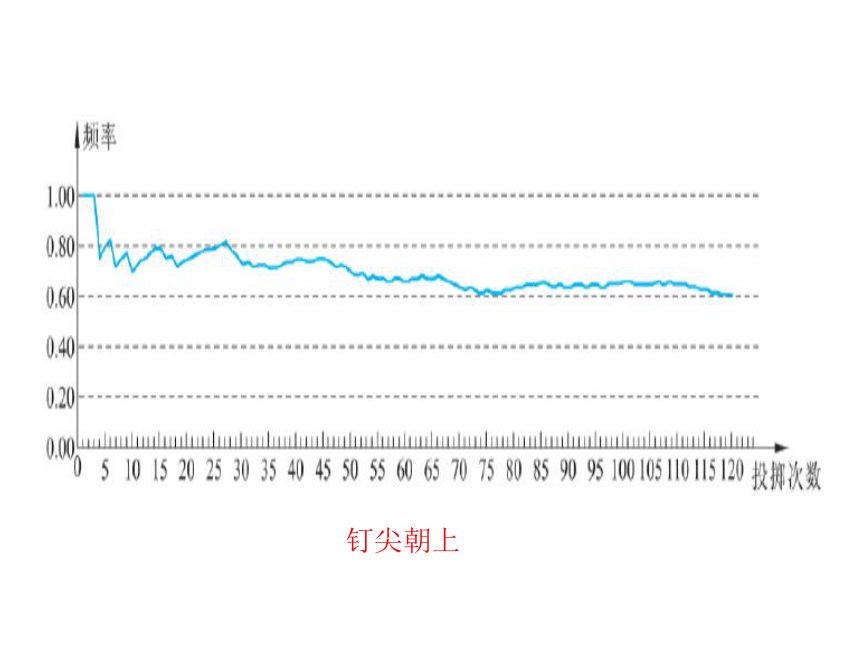
从一定的高度落下的图钉,落地后可能图钉尖着地,也可能图钉尖不找地,估计一下哪种事件的概率更大,与同学合作,通过做实验来验证
一下你事先估计是否正确?
你能估计图钉尖朝上的概率吗?
大家都来做一做
钉尖朝上
用列举法计算概率
问题1.掷一枚硬币,落地后会出现几种结果?
。正面向上、反面向上,2种可能性相等
问题2.掷两枚硬币(硬币A,硬币B),落地后会出现几种结果?
。A正B正,A正B反,A反B正,A反B反,四种可能性相等。
为了既不重复,又不遗漏地列举出所有这些等可能的结果,还有比较简便的方法吗?
10.2 用列举法计算概率(1)
开始
硬币A 正面 反面
硬币B 正面 反面 正面 反面
由图可知,抛掷硬币A、硬币B落地后共有四种可能结果(正面,正面),(正面,反面),(反面,正面),(反面,反面)
请仔细观察:
上图像一棵倒立的树,我们把它称为树状图。我们会发现:从上到下每一条路径就是一种可能结果,并且每种结果发生的可能性相同。
(反面,反面)
(反面,正面)
(正面,反面)
(正面,正面)
硬币A
正面
反面
硬币B 正面 反面
由上表可知,抛掷硬币A、硬币B落地后共有四种可能结果(正面,正面),(正面,反面),(反面,正面),(反面,反面)
上表中第一列表示抛掷硬币A 出现正面、反面两种可能,第一行表示抛掷硬币B出现正面、反面两种可能,从而在表中列出了所有等可能的4种结果。
例1 在A、B两个盒子中都装入分别写有数字1,2的两张卡片,分别从每个盒子中任取一张卡片,两张卡片上的数字之和为3的概率是多少?
解:画出树状图 开始
A盒 1 2
B盒 1 2 1 2
试一试
由图可知,有4种等可能的结果 ,其中两数和为3的结果有 种,即 。
所以P(和为3)= =
(1,1),(1,2),(2,1),(2,2)
(1,2),(2,1)
2
试一试 将一个均匀的硬币上抛三次,结果两次正面朝上,一次反面朝上的概率________.
解:
开始
反
正
正
反
反
正
正
反
反
反
正
反
正
正
第一次:
第二次:
第三次:
3/8
幻灯片 7
要“玩”出水平
做一做
2
“配紫色”游戏
小明为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
真知灼见源于实践
议一议
3
树状图可以是:
“配紫色”游戏
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
游戏者获胜的概率是1/6.
真知灼见源于实践
想一想
4
表格可以是:
“配紫色”游戏
游戏者获胜的概率是1/6.
第二个
转盘
第一个
转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
1200
红
红
蓝
蓝
真知灼见源于实践
想一想
5
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
是“玩家”就玩出水平
想一想
6
“配紫色”游戏的变异
小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2.
1200
红1
红
蓝
蓝
红2
你认为谁做的对 说说你的理由.
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
是“玩家”就玩出水平
议一议
6
由“配紫色”游戏的变异想到的
1200
红1
红
蓝
蓝
红2
小颖的做法不正确.因为左边的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.
1200
红
红
蓝
蓝
用树状图和列表的方法求概率时应注意些什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
行家看“门道”
例题欣赏
7
例2 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
用心领“悟”
1
2
3
行家看“门道”
例题欣赏
8
学以致用
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
用树状图怎么解答例2 请用行动来证明“我能行”.
理性的结论源于实践操作
是真是假,事实说话
设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为1/3.
随堂练习
7
具体要求:
1. 根的判别式的推导过程是什么?在应用时应注意哪些问题?
2.重点:例1(3)拓展(一)例2 拓展(二)巩固练习1(5 ) 2
合作探究(6分钟)
明确目标:
A层同学注重方法的总结,并适当拓展延伸,目标达成 率120%。
B层同学注重运用基础知识解决问题,目标达成100%。
C层同学注重基础知识,掌握探究1-2,目标达成率80%。
方式:
1.先一对一讨论,再组内互相交流,疑问用红笔 标出。
2. 注意总结题目的解题规律、方法和易错点 ,提前讨论完的小组坐下改错并全部达成目标,多拓展, 注重总结与掌握 。
3. 小组长做好展示、点评分工。
高效展示
展示内容 展示小组
前黑板:例1(3) 2A2
前黑板:拓展(一) 7B2
后黑板:例2 1B1
后黑板:拓展(二) 6A2
侧黑板:巩固练习1(5) 4A2
侧黑板 巩固练习2 5B2
:
要求:⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、 规范。
⑵非展示同学巩固基础知识、整理落实学案,做好拓展。不浪费一分钟,小组长做好安排和检查。
精彩点评
要求:⑴先点评对错;再点评思路方法,应该注意的问题,力争进行必要的变形拓展。
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑。
点评内容 点评小组
前黑板:例1(3) 5A1
前黑板:拓展(一) 6A1
后黑板:例2 7A1
后黑板:拓展(二) 4A1
侧黑板:巩固练习1(5) 3A1
侧黑板 巩固练习2 1A1
挑战记忆
m为事件A可能发生的结果数
n为所有等可能结果的总数
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
课堂评价
学科班长:1.回扣目标 总结收获
2.评出优秀小组和个人
请拿出你的导学案,课本,双色笔,典型题本还有你的激情、动力和目标
全力投入会使你与众不同
你是最优秀的,你一定能做的更好!
温馨提示
必然事件
不可能事件
可能性
0 (50%) 1(100%)
不可能发生
可能发生
必然发生
不确定事件 (随机事件)
回顾
挑战记忆
确定事件
概率 事件发生的可能性,也称为事件发生的概率.
必然事件发生的概率为1(或100%),
记作P(必然事件)=1;
不可能事件发生的概率为0,
记作P(不可能事件)=0;
随机事件(不确定事件)发生的概率介于0~1之 间,即0
那么0
m为事件A可能发生的结果数
n为所有等可能结果的总数
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
频数:每个对象出现的次数
频率:每个对象出现的次数 与总次数
的比值
问题1.掷一枚硬币,落地后会出现几种结果?
。正面向上、反面向上,2种可能性相等
问题2.掷两枚硬币(硬币A,硬币B),落地后会出现几种结果?
。A正B正,A正B反,A反B正,A反B反,四种可能性相等。
材料1:
则估计抛掷一枚硬币正面朝上的概率为__
o.5
两个正面 一正一反 两个反面
频数 502 1000 498
频率 0.251 0.5 0.249
某人掷两枚硬币2000次的结果
概率分别为 0.25 0.5 0.25
在进行大量重复试验时,随着实验次数的增加,
一个不确定事件发生的频率会逐渐稳定到某一个数值。
我们可以用平稳时的频率来估计这个事件发生的概率.
结论
从一定的高度落下的图钉,落地后可能图钉尖着地,也可能图钉尖不找地,估计一下哪种事件的概率更大,与同学合作,通过做实验来验证
一下你事先估计是否正确?
你能估计图钉尖朝上的概率吗?
大家都来做一做
钉尖朝上
用列举法计算概率
问题1.掷一枚硬币,落地后会出现几种结果?
。正面向上、反面向上,2种可能性相等
问题2.掷两枚硬币(硬币A,硬币B),落地后会出现几种结果?
。A正B正,A正B反,A反B正,A反B反,四种可能性相等。
为了既不重复,又不遗漏地列举出所有这些等可能的结果,还有比较简便的方法吗?
10.2 用列举法计算概率(1)
开始
硬币A 正面 反面
硬币B 正面 反面 正面 反面
由图可知,抛掷硬币A、硬币B落地后共有四种可能结果(正面,正面),(正面,反面),(反面,正面),(反面,反面)
请仔细观察:
上图像一棵倒立的树,我们把它称为树状图。我们会发现:从上到下每一条路径就是一种可能结果,并且每种结果发生的可能性相同。
(反面,反面)
(反面,正面)
(正面,反面)
(正面,正面)
硬币A
正面
反面
硬币B 正面 反面
由上表可知,抛掷硬币A、硬币B落地后共有四种可能结果(正面,正面),(正面,反面),(反面,正面),(反面,反面)
上表中第一列表示抛掷硬币A 出现正面、反面两种可能,第一行表示抛掷硬币B出现正面、反面两种可能,从而在表中列出了所有等可能的4种结果。
例1 在A、B两个盒子中都装入分别写有数字1,2的两张卡片,分别从每个盒子中任取一张卡片,两张卡片上的数字之和为3的概率是多少?
解:画出树状图 开始
A盒 1 2
B盒 1 2 1 2
试一试
由图可知,有4种等可能的结果 ,其中两数和为3的结果有 种,即 。
所以P(和为3)= =
(1,1),(1,2),(2,1),(2,2)
(1,2),(2,1)
2
试一试 将一个均匀的硬币上抛三次,结果两次正面朝上,一次反面朝上的概率________.
解:
开始
反
正
正
反
反
正
正
反
反
反
正
反
正
正
第一次:
第二次:
第三次:
3/8
幻灯片 7
要“玩”出水平
做一做
2
“配紫色”游戏
小明为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
真知灼见源于实践
议一议
3
树状图可以是:
“配紫色”游戏
开始
红
白
黄
蓝
绿
(红,黄)
(红,蓝)
(红,绿)
(白,黄)
(白,蓝)
(白,绿)
黄
蓝
绿
游戏者获胜的概率是1/6.
真知灼见源于实践
想一想
4
表格可以是:
“配紫色”游戏
游戏者获胜的概率是1/6.
第二个
转盘
第一个
转盘
黄
蓝
绿
红
(红,黄)
(红,蓝)
(红,绿)
白
(白,黄)
(白,蓝)
(白,绿)
1200
红
红
蓝
蓝
真知灼见源于实践
想一想
5
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
是“玩家”就玩出水平
想一想
6
“配紫色”游戏的变异
小亮则先把左边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2.
1200
红1
红
蓝
蓝
红2
你认为谁做的对 说说你的理由.
红色 蓝色
红色1 (红1,红) (红1,蓝)
红色2 (红2,红) (红2,蓝)
蓝色 (蓝,红) (蓝,蓝)
是“玩家”就玩出水平
议一议
6
由“配紫色”游戏的变异想到的
1200
红1
红
蓝
蓝
红2
小颖的做法不正确.因为左边的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.
1200
红
红
蓝
蓝
用树状图和列表的方法求概率时应注意些什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同.
行家看“门道”
例题欣赏
7
例2 如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
用心领“悟”
1
2
3
行家看“门道”
例题欣赏
8
学以致用
解:每次游戏时,所有可能出现的结果如下:
总共有6种结果,每种结果出现的可能性相同,而所摸球上的数字与转盘转出的数字之和为2的结果只有一种:(1,1),因此游戏者获胜的概率为1/6.
转盘
摸球
1
1
2
(1,1)
(1,2)
2
(2,1)
(2,2)
3
(1,3)
(2,3)
用树状图怎么解答例2 请用行动来证明“我能行”.
理性的结论源于实践操作
是真是假,事实说话
设计两个转盘做“配紫色”游戏,使游戏者获胜的概率为1/3.
随堂练习
7
具体要求:
1. 根的判别式的推导过程是什么?在应用时应注意哪些问题?
2.重点:例1(3)拓展(一)例2 拓展(二)巩固练习1(5 ) 2
合作探究(6分钟)
明确目标:
A层同学注重方法的总结,并适当拓展延伸,目标达成 率120%。
B层同学注重运用基础知识解决问题,目标达成100%。
C层同学注重基础知识,掌握探究1-2,目标达成率80%。
方式:
1.先一对一讨论,再组内互相交流,疑问用红笔 标出。
2. 注意总结题目的解题规律、方法和易错点 ,提前讨论完的小组坐下改错并全部达成目标,多拓展, 注重总结与掌握 。
3. 小组长做好展示、点评分工。
高效展示
展示内容 展示小组
前黑板:例1(3) 2A2
前黑板:拓展(一) 7B2
后黑板:例2 1B1
后黑板:拓展(二) 6A2
侧黑板:巩固练习1(5) 4A2
侧黑板 巩固练习2 5B2
:
要求:⑴口头展示,声音洪亮、清楚;书面展示要分层次、要点化,书写要认真、 规范。
⑵非展示同学巩固基础知识、整理落实学案,做好拓展。不浪费一分钟,小组长做好安排和检查。
精彩点评
要求:⑴先点评对错;再点评思路方法,应该注意的问题,力争进行必要的变形拓展。
⑵其他同学认真倾听、积极思考、记好笔记、大胆质疑。
点评内容 点评小组
前黑板:例1(3) 5A1
前黑板:拓展(一) 6A1
后黑板:例2 7A1
后黑板:拓展(二) 4A1
侧黑板:巩固练习1(5) 3A1
侧黑板 巩固练习2 1A1
挑战记忆
m为事件A可能发生的结果数
n为所有等可能结果的总数
(1)实验的所有结果是有限个(n)
(2)各种结果的可能性相等.
课堂评价
学科班长:1.回扣目标 总结收获
2.评出优秀小组和个人
