1.1.2空间向量的数量积运算(共36张PPT)
文档属性
| 名称 | 1.1.2空间向量的数量积运算(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 626.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:49:50 | ||
图片预览










文档简介
(共36张PPT)
1.1.2
空间向量的数量积运算
平面向量及其线性运算
空间向量及其线性运算
推
广
平面向量的数量积运算
空间向量的数量积运算
问题1
你能类比平面向量的数量积运算,把它推广到空间向量吗?
追问(1)
学习平面向量时,我们是如何研究它的数量积运算的?
夹角
数量积的定义
运算律
应用
追问(2)
什么是平面向量的夹角?你能类比平面向量,给出空间向量夹角的概念吗?
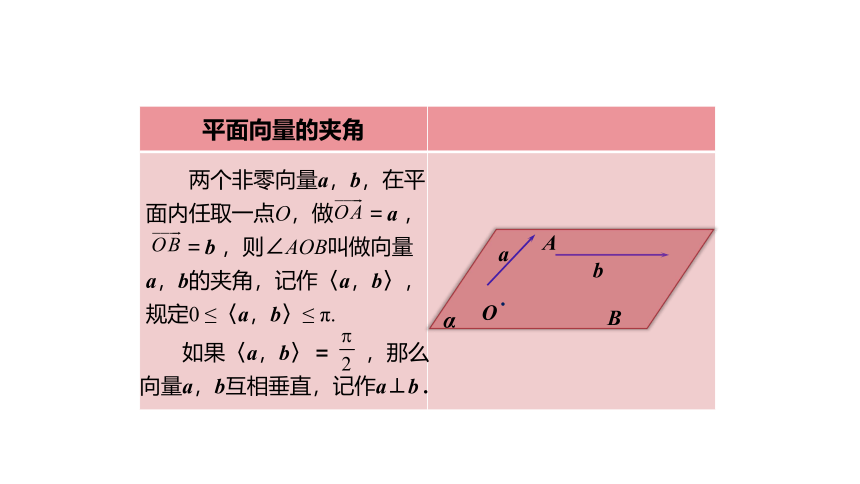
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做
=a
,
=b
,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0
≤〈a,b〉≤
π.
如果〈a,b〉=
,那么向量a,b互相垂直,记作a⊥b
.
b
a
.
O
α
A
B
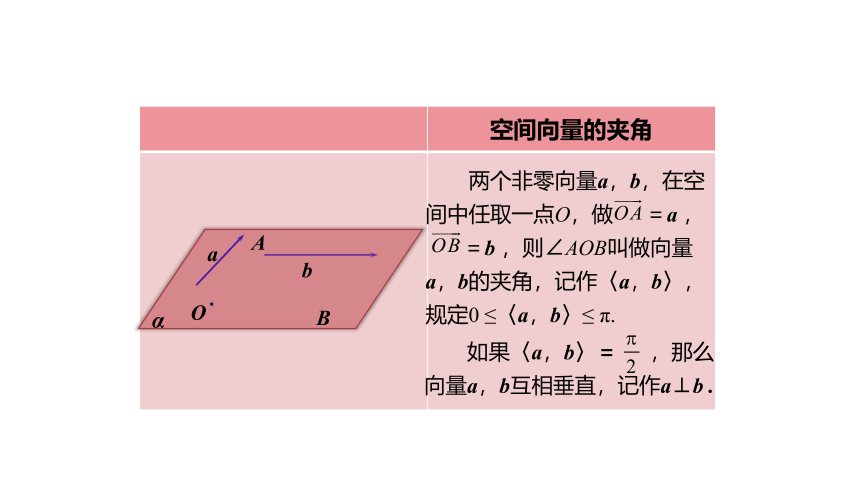
空间向量的夹角
两个非零向量a,b,在空间中任取一点O,做
=a
,
=b
,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0
≤〈a,b〉≤
π.
如果〈a,b〉=
,那么向量a,b互相垂直,记作a⊥b
.
b
a
.
O
α
A
B
两个非零平面向量的数量积是一个实数,等于这两个向量的模和它们夹角余弦值的乘积,即:
a
·
b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
追问(3)
平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间向量的数量积
已知非零向量a,b,|a||b|cos〈a,b〉叫做a,b的数量积(inner
product),记作a
·
b
.
即
a
·
b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
追问(3)
平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间向量的数量积的性质
①
若a,b是非零向量,a⊥b
?
a
·
b=0;
②
a
·
a=a
2=|a||a|cos〈a,a〉=|a|2
.
③若a与b同向,则a·b=______;若反向,则a·b=________.
④
若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
证明空间中的垂直关系
求空间中线段的长度
追问(3)
平面向量的数量积有哪些性质?你能类比平面向量,给出空间向量数量积的性质吗?
|a|·|b|
-|a|·|b|
求向量的夹角
追问(4)
平面向量的数量积运算有哪些运算律?
平面向量的数量积运算律
①
(λa)·b=λ(a·b),
λ∈R;
②
a·b=b·a(交换律);
③
a·(b+c)=a·b+a·c(分配律).
追问(4)
类比平面向量,你能得出空间向量的数量积运算有哪些运算律?
空间向量的数量积运算律
①
(λa)
·b=λ(a·b),
λ∈R;
②
a·b=b·a(交换律);
③
a·(b+c)=a·b+a·c(分配律).
追问(5)
在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
b
a
A
B
A1
D
C
B1
b
a
.
O
N
M
M1
=|a|cos〈a,b〉
平面向量的投影
两个非零向量a,b,
=a,
=b,过A和B分别做
所在直线的垂线,垂足分别为A1和B1,得到
,称上述变换为向量a向向量b的投影,
叫向量a在向量b上的投影向量.
b
a
A
B
A1
D
C
B1
b
a
.
O
α
a
c
追问(5)
在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
空间向量的投影向量
将空间向量a,b
,平移到同一个平面α内,利用平面上向量的投影得到与向量b共线的向量c,即:
c
=|a|cos〈a,b〉
,
向量c称为向量a在向量b上的投影向量.
问题2
空间向量的数量积运算由平面向量的数量积运算推广而来,与平面向量数量积运算一样,要注意它与向量的线性运算、实数的乘法运算的区别.你能回答以下问题吗?
追问(1)
由a·b=0,能否得到a=0或
b=0?
不一定!
因为
a·b=|a||b|cos〈a,b〉=0,
所以|a|=0或|b|=0或cos〈a,b〉=0.
即a=0或b=0或a⊥b.
追问(2)
对于三个均不为零的实数a,b,c,若ab=ac,则b=c.
对于非零向量a,b,c,由a·b=a·c,能得到b=c吗?
不一定!
由a·b
=
a·c,有a·(b-c)=0.
从而有b=c或a⊥(b-c).
追问(3)
对于三个均不为零的数a,b,c,若ab=c,则
或
.那么对于向量a,b,若a·b=k,能写成
或
吗?
不能!因为没有定义向量的除法运算.
k
k
追问(4)
对于三个均不为零的数a,b,c,有(ab)c=a(bc).对于向量a,b,c,(a·b)c=a(b·c)成立吗?
不一定!两个向量的数量积为一个实数,(a·b)c和a(b·c)分别表示与向量c和向量a共线的向量,它们不一定相等.
向量的数量积运算没有结合律.
问题3
用空间向量的数量积运算,可以解决空间中的哪些问题?
追问
空间向量的数量积运算可以解决哪些问题?
平面向量数量积的应用
空间向量数量积的应用
(1)求线段长度(距离):
(2)求夹角:
(3)证明垂直:
把所求线段看成一个向量的模,并用已知向量表示所求向量,再用数量积运算求该向量的模;
a⊥b
?
a
·
b=0.
cos
〈a,b〉=
;
问题4
如右图,在平行六面体ABCD-A'B'C'D'中,AB
=
5,
AD
=
3,AA'=
7,∠BAD
=
60°,∠BAA'=
∠DAA'=
45°.
求:
(1)
;(2)
AC'的长(精确到0.1).
追问(1)
如何计算
?它们的长度,夹角是多少?
AB,AD的长度和夹角均已知,AB=5,AD=3,
∠BAD
=
60°.
解:(1)
追问(2)
为了求AC'的长,应该用哪些向量表示
?为什么?如何表示?
可以根据已知条件与平行四边形法则,用
来表示,因为它们的模长和夹角均已知,可以进行数量积运算.
(2)
先用已知向量表示所求向量,
再由数量积运算求模长,
是立体几何中求线段长度的常用向量方法.
问题5
如右图,m,n是平面α内的两条相交直线.
如果l⊥m,
l⊥n,
求证:
l⊥平面α;
m
n
l
α
追问(1)
直线和平面垂直的定义是什么?
m
n
l
α
如果直线l和平面α内的任意一条直线都垂直,则
直线l垂直于平面α
.
追问(2)
如何用向量方法证明l和平面α内任意一条直线垂直?
m
n
l
α
在平面α内任取一条直线g,分别在直线l,m,n,g
上取非零向量l,m,n,g作为方向向量,由向量共面的
充要条件知,g可由m,n的线性组合表示.
由已知l⊥m,
l⊥n,通过数量积运算,得到l⊥g,从而l⊥g,
从而l⊥平面α.
g
m
g
n
l
m
n
l
α
g
m
g
n
l
证明:
在平面α内作任意直线g,分别在直线l,m,n,g上取非零向量l,m,n,g.
因为直线m,n相交,所以m,n不共线.
因此,存在唯一有序实数对(x,y),使得g=xm
+yn.
因为l⊥m,
l⊥n,所以l⊥m,
l⊥n,即l·m=0,l·n=0.
于是l·g=l·xn+
l·ym=xl·n+yl·m=0,
所以l⊥g.
即l⊥g,所以l⊥平面α.
在表示直线上取非零向量,用向量数量积为零刻画直线的垂直,是立体几何中的常用向量方法.
m
n
l
α
g
m
g
n
l
练习
A
B
A1
C1
B1
C
(1).如图,在正三棱柱ABC-A1B1C1
中,若AB=
BB1,则AB1与C1B所成角的大小为(
)
A.
B.
C.
D.
B
问题6
回顾本节课的探究过程,你学到了什么?
1
空间向量的数量积运算
(1)
空间向量数量积运算的定义;
(2)
空间向量数量积运算的运算律;
(3)
空间向量数量积运算的应用.
2
类比平面向量的研究方法
类比
猜想
证明或转化
推广
课后作业
用投影向量证明空间向量数量积运算的分配律;
2.
教材P9-10,习题1.1第4,7,10题.
1.1.2
空间向量的数量积运算
平面向量及其线性运算
空间向量及其线性运算
推
广
平面向量的数量积运算
空间向量的数量积运算
问题1
你能类比平面向量的数量积运算,把它推广到空间向量吗?
追问(1)
学习平面向量时,我们是如何研究它的数量积运算的?
夹角
数量积的定义
运算律
应用
追问(2)
什么是平面向量的夹角?你能类比平面向量,给出空间向量夹角的概念吗?
平面向量的夹角
两个非零向量a,b,在平面内任取一点O,做
=a
,
=b
,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0
≤〈a,b〉≤
π.
如果〈a,b〉=
,那么向量a,b互相垂直,记作a⊥b
.
b
a
.
O
α
A
B
空间向量的夹角
两个非零向量a,b,在空间中任取一点O,做
=a
,
=b
,则∠AOB叫做向量
a,b的夹角,记作〈a,b〉,规定0
≤〈a,b〉≤
π.
如果〈a,b〉=
,那么向量a,b互相垂直,记作a⊥b
.
b
a
.
O
α
A
B
两个非零平面向量的数量积是一个实数,等于这两个向量的模和它们夹角余弦值的乘积,即:
a
·
b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
追问(3)
平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间向量的数量积
已知非零向量a,b,|a||b|cos〈a,b〉叫做a,b的数量积(inner
product),记作a
·
b
.
即
a
·
b=|a||b|cos〈a,b〉.
特别地,零向量与任意向量的数量积为0.
追问(3)
平面向量的数量积是什么?你能类比平面向量,给出空间向量数量积的运算吗?
空间向量的数量积的性质
①
若a,b是非零向量,a⊥b
?
a
·
b=0;
②
a
·
a=a
2=|a||a|cos〈a,a〉=|a|2
.
③若a与b同向,则a·b=______;若反向,则a·b=________.
④
若〈a,b〉为a,b的夹角,则cos〈a,b〉=_______
⑤|a·b|≤|a|·|b|
证明空间中的垂直关系
求空间中线段的长度
追问(3)
平面向量的数量积有哪些性质?你能类比平面向量,给出空间向量数量积的性质吗?
|a|·|b|
-|a|·|b|
求向量的夹角
追问(4)
平面向量的数量积运算有哪些运算律?
平面向量的数量积运算律
①
(λa)·b=λ(a·b),
λ∈R;
②
a·b=b·a(交换律);
③
a·(b+c)=a·b+a·c(分配律).
追问(4)
类比平面向量,你能得出空间向量的数量积运算有哪些运算律?
空间向量的数量积运算律
①
(λa)
·b=λ(a·b),
λ∈R;
②
a·b=b·a(交换律);
③
a·(b+c)=a·b+a·c(分配律).
追问(5)
在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
b
a
A
B
A1
D
C
B1
b
a
.
O
N
M
M1
=|a|cos〈a,b〉
平面向量的投影
两个非零向量a,b,
=a,
=b,过A和B分别做
所在直线的垂线,垂足分别为A1和B1,得到
,称上述变换为向量a向向量b的投影,
叫向量a在向量b上的投影向量.
b
a
A
B
A1
D
C
B1
b
a
.
O
α
a
c
追问(5)
在平面向量中我们学习过投影向量的概念,什么是投影向量?你能把它推广到空间向量中吗?
空间向量的投影向量
将空间向量a,b
,平移到同一个平面α内,利用平面上向量的投影得到与向量b共线的向量c,即:
c
=|a|cos〈a,b〉
,
向量c称为向量a在向量b上的投影向量.
问题2
空间向量的数量积运算由平面向量的数量积运算推广而来,与平面向量数量积运算一样,要注意它与向量的线性运算、实数的乘法运算的区别.你能回答以下问题吗?
追问(1)
由a·b=0,能否得到a=0或
b=0?
不一定!
因为
a·b=|a||b|cos〈a,b〉=0,
所以|a|=0或|b|=0或cos〈a,b〉=0.
即a=0或b=0或a⊥b.
追问(2)
对于三个均不为零的实数a,b,c,若ab=ac,则b=c.
对于非零向量a,b,c,由a·b=a·c,能得到b=c吗?
不一定!
由a·b
=
a·c,有a·(b-c)=0.
从而有b=c或a⊥(b-c).
追问(3)
对于三个均不为零的数a,b,c,若ab=c,则
或
.那么对于向量a,b,若a·b=k,能写成
或
吗?
不能!因为没有定义向量的除法运算.
k
k
追问(4)
对于三个均不为零的数a,b,c,有(ab)c=a(bc).对于向量a,b,c,(a·b)c=a(b·c)成立吗?
不一定!两个向量的数量积为一个实数,(a·b)c和a(b·c)分别表示与向量c和向量a共线的向量,它们不一定相等.
向量的数量积运算没有结合律.
问题3
用空间向量的数量积运算,可以解决空间中的哪些问题?
追问
空间向量的数量积运算可以解决哪些问题?
平面向量数量积的应用
空间向量数量积的应用
(1)求线段长度(距离):
(2)求夹角:
(3)证明垂直:
把所求线段看成一个向量的模,并用已知向量表示所求向量,再用数量积运算求该向量的模;
a⊥b
?
a
·
b=0.
cos
〈a,b〉=
;
问题4
如右图,在平行六面体ABCD-A'B'C'D'中,AB
=
5,
AD
=
3,AA'=
7,∠BAD
=
60°,∠BAA'=
∠DAA'=
45°.
求:
(1)
;(2)
AC'的长(精确到0.1).
追问(1)
如何计算
?它们的长度,夹角是多少?
AB,AD的长度和夹角均已知,AB=5,AD=3,
∠BAD
=
60°.
解:(1)
追问(2)
为了求AC'的长,应该用哪些向量表示
?为什么?如何表示?
可以根据已知条件与平行四边形法则,用
来表示,因为它们的模长和夹角均已知,可以进行数量积运算.
(2)
先用已知向量表示所求向量,
再由数量积运算求模长,
是立体几何中求线段长度的常用向量方法.
问题5
如右图,m,n是平面α内的两条相交直线.
如果l⊥m,
l⊥n,
求证:
l⊥平面α;
m
n
l
α
追问(1)
直线和平面垂直的定义是什么?
m
n
l
α
如果直线l和平面α内的任意一条直线都垂直,则
直线l垂直于平面α
.
追问(2)
如何用向量方法证明l和平面α内任意一条直线垂直?
m
n
l
α
在平面α内任取一条直线g,分别在直线l,m,n,g
上取非零向量l,m,n,g作为方向向量,由向量共面的
充要条件知,g可由m,n的线性组合表示.
由已知l⊥m,
l⊥n,通过数量积运算,得到l⊥g,从而l⊥g,
从而l⊥平面α.
g
m
g
n
l
m
n
l
α
g
m
g
n
l
证明:
在平面α内作任意直线g,分别在直线l,m,n,g上取非零向量l,m,n,g.
因为直线m,n相交,所以m,n不共线.
因此,存在唯一有序实数对(x,y),使得g=xm
+yn.
因为l⊥m,
l⊥n,所以l⊥m,
l⊥n,即l·m=0,l·n=0.
于是l·g=l·xn+
l·ym=xl·n+yl·m=0,
所以l⊥g.
即l⊥g,所以l⊥平面α.
在表示直线上取非零向量,用向量数量积为零刻画直线的垂直,是立体几何中的常用向量方法.
m
n
l
α
g
m
g
n
l
练习
A
B
A1
C1
B1
C
(1).如图,在正三棱柱ABC-A1B1C1
中,若AB=
BB1,则AB1与C1B所成角的大小为(
)
A.
B.
C.
D.
B
问题6
回顾本节课的探究过程,你学到了什么?
1
空间向量的数量积运算
(1)
空间向量数量积运算的定义;
(2)
空间向量数量积运算的运算律;
(3)
空间向量数量积运算的应用.
2
类比平面向量的研究方法
类比
猜想
证明或转化
推广
课后作业
用投影向量证明空间向量数量积运算的分配律;
2.
教材P9-10,习题1.1第4,7,10题.
