1.2空间向量基本定理(共26张PPT)
文档属性
| 名称 | 1.2空间向量基本定理(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 535.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 09:51:03 | ||
图片预览







文档简介
(共26张PPT)
1.2
空间向量基本定理
一、复习回顾、提出问题
问题:空间中,任意一个空间向量能否用任意三个不共面的向量
来表示呢?
平面向量基本定理
如果
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数
,使
.
若
不共线,我们把
叫做表示这一平面内所有向量的一个基底.
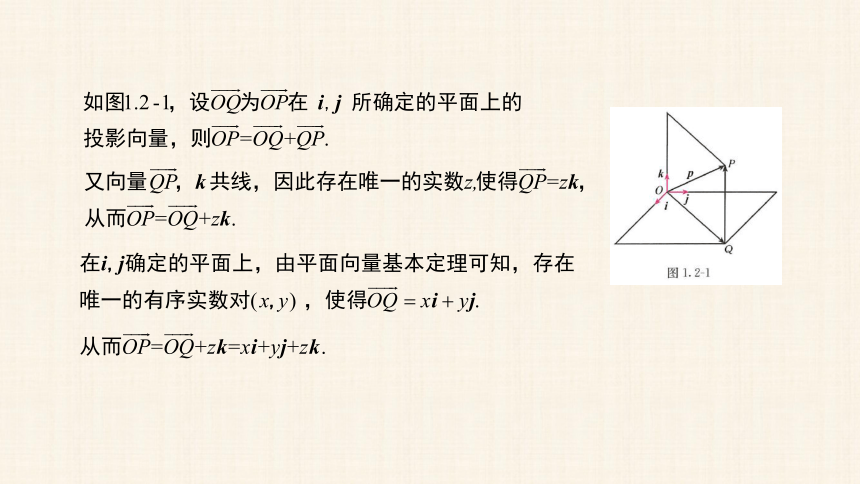
如图,设
是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点
,对于任意一个空间向量
,
能否用
表示呢?
O
i
j
p
P
k
二、探究新知
因此,如果
是空间三个两两垂直的向量,那么对于任意一个空间向量
,存在唯一的有序实数组
,使得
.
我们称
分别为向量
在
上的分向量.
探究
在空间中,如果用任意三个不共面的向量
代替两两垂直的向量
,你能得出类似的结论吗?
空间向量基本定理
如果三个向量
不共面,那么对
任意一个空间向量
,存在唯一的有序实数组
,
使得
我们把
叫做空间的一个基底,
都叫做基向量.
所有空间向量组成的集合就是
空间任意三个不共面的向量都可以构成空间的一个基底。
单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用
表示.
空间向量的正交分解
由空间向量基本定理可知,对空间中的任意向量
,均可以分解为三个向量
,使
,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
(1)构成空间的基底是唯一的吗?
(2)基底选定后,空间中向量用基底表示,表示形式唯一吗?
(3)基向量可以为零向量吗?
思考
答案:不唯一
答案:唯一
答案:不可以.因为零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面.
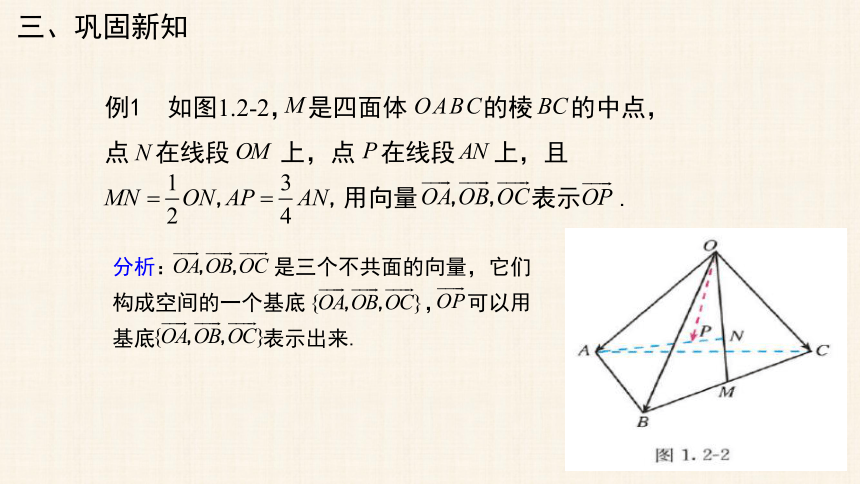
例1
如图1.2-2,
是四面体
的棱
的中点,
点
在线段
上,点
在线段
上,且
用向量
表示
.
分析:
是三个不共面的向量,它们
构成空间的一个基底
,
可以用
基底
表示出来.
三、巩固新知
解:
1.
已知向量
是空间的一个基底,从
中选哪一个向量,一定可以与向量
构成空间的另一个基底?
练习
解:向量
与
一定构成空间的一个基底.否则
与
共面,
即
与
共面,于是
与
共面,这与已知矛盾.
2.
已知
为空间的四个点,且向量
不构成空间的一个基底,那么点
是否共面?
解:共面
3.
如图,已知平行六面体
点
是侧面
的中心,且
用向量
表示下列向量:
解:
问题:怎样用向量的方法解决异面直线的垂直问题呢?
要证直线垂直,只要证直线的方向向量的数量积等于零.
利用向量数量积证明线线垂直的步骤:
1.找到所证直线的方向向量;
2.用已知向量表示所证向量;
3.结合数量积公式和运算律证数量积等于0;
4.将向量问题回归到几何问题。
1.空间向量基本定理及其意义
2.单位正交基底、空间向量正交分解
3.体会类比、转化的数学思想,所有空间向量间的运算转化为基向量间的运算,为几何问题代数化奠定了基础.
空间向量基本定理
如果三个向量
不共面,那么对任意一个空间向量
,存在唯一的有序实数组
,使得
我们把
叫做空间的一个基底,
都叫做基向量.
五、总结提升
教科书第15页习题1.2第1,2,3,4题
六、布置作业
谢
谢!
1.2
空间向量基本定理
一、复习回顾、提出问题
问题:空间中,任意一个空间向量能否用任意三个不共面的向量
来表示呢?
平面向量基本定理
如果
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数
,使
.
若
不共线,我们把
叫做表示这一平面内所有向量的一个基底.
如图,设
是空间中三个两两垂直的向量,且表示它们的有向线段有公共起点
,对于任意一个空间向量
,
能否用
表示呢?
O
i
j
p
P
k
二、探究新知
因此,如果
是空间三个两两垂直的向量,那么对于任意一个空间向量
,存在唯一的有序实数组
,使得
.
我们称
分别为向量
在
上的分向量.
探究
在空间中,如果用任意三个不共面的向量
代替两两垂直的向量
,你能得出类似的结论吗?
空间向量基本定理
如果三个向量
不共面,那么对
任意一个空间向量
,存在唯一的有序实数组
,
使得
我们把
叫做空间的一个基底,
都叫做基向量.
所有空间向量组成的集合就是
空间任意三个不共面的向量都可以构成空间的一个基底。
单位正交基底
如果空间的一个基底中的三个基向量两两垂直,且长度都为1,那么这个基底叫做单位正交基底,常用
表示.
空间向量的正交分解
由空间向量基本定理可知,对空间中的任意向量
,均可以分解为三个向量
,使
,像这样,把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.
(1)构成空间的基底是唯一的吗?
(2)基底选定后,空间中向量用基底表示,表示形式唯一吗?
(3)基向量可以为零向量吗?
思考
答案:不唯一
答案:唯一
答案:不可以.因为零向量与任意一个非零向量共线,与任意两个不共线的非零向量共面.
例1
如图1.2-2,
是四面体
的棱
的中点,
点
在线段
上,点
在线段
上,且
用向量
表示
.
分析:
是三个不共面的向量,它们
构成空间的一个基底
,
可以用
基底
表示出来.
三、巩固新知
解:
1.
已知向量
是空间的一个基底,从
中选哪一个向量,一定可以与向量
构成空间的另一个基底?
练习
解:向量
与
一定构成空间的一个基底.否则
与
共面,
即
与
共面,于是
与
共面,这与已知矛盾.
2.
已知
为空间的四个点,且向量
不构成空间的一个基底,那么点
是否共面?
解:共面
3.
如图,已知平行六面体
点
是侧面
的中心,且
用向量
表示下列向量:
解:
问题:怎样用向量的方法解决异面直线的垂直问题呢?
要证直线垂直,只要证直线的方向向量的数量积等于零.
利用向量数量积证明线线垂直的步骤:
1.找到所证直线的方向向量;
2.用已知向量表示所证向量;
3.结合数量积公式和运算律证数量积等于0;
4.将向量问题回归到几何问题。
1.空间向量基本定理及其意义
2.单位正交基底、空间向量正交分解
3.体会类比、转化的数学思想,所有空间向量间的运算转化为基向量间的运算,为几何问题代数化奠定了基础.
空间向量基本定理
如果三个向量
不共面,那么对任意一个空间向量
,存在唯一的有序实数组
,使得
我们把
叫做空间的一个基底,
都叫做基向量.
五、总结提升
教科书第15页习题1.2第1,2,3,4题
六、布置作业
谢
谢!
