华东师大版数学九年级上册 23.4中位线 课件(共33张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.4中位线 课件(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览






文档简介
(共33张PPT)
学习目标
知识与技能:理解三角形中位线定义与性质,会应用三角形中位线解决实际问题.
过程与方法:经历探究三角形中位线定义、性质的过程,感受三角形中位线定理的应用思想。
情感、态度与价值观:培养良好的探究意识和合作交流的习惯,体会数学推理的应用价值.
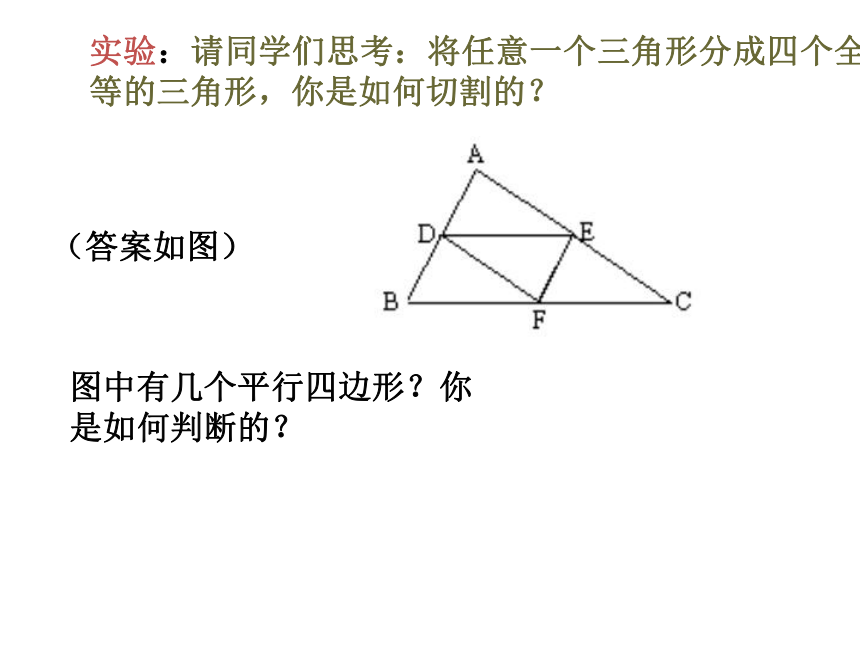
实验:请同学们思考:将任意一个三角形分成四个全等的三角形,你是如何切割的?
图中有几个平行四边形?你是如何判断的?
(答案如图)
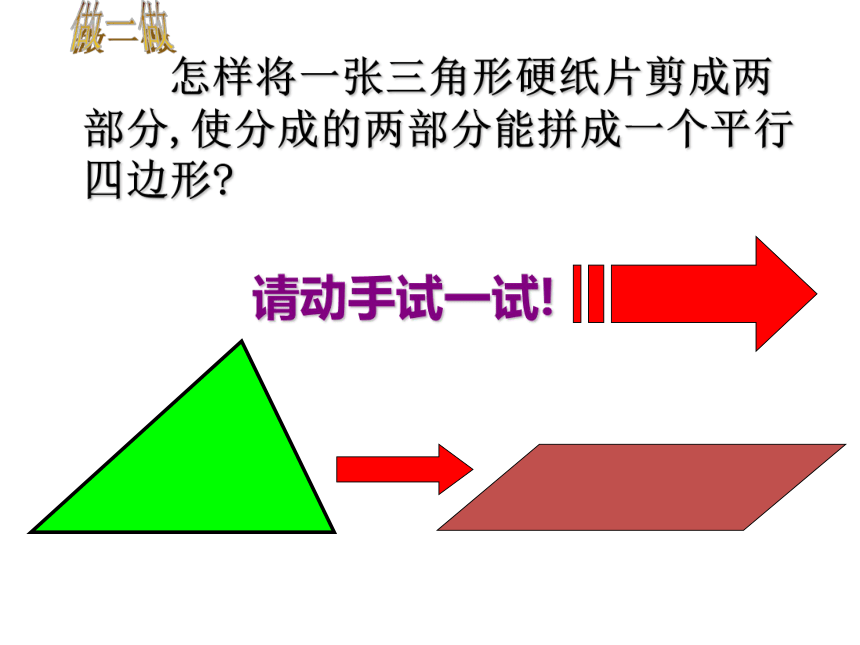
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
请动手试一试!
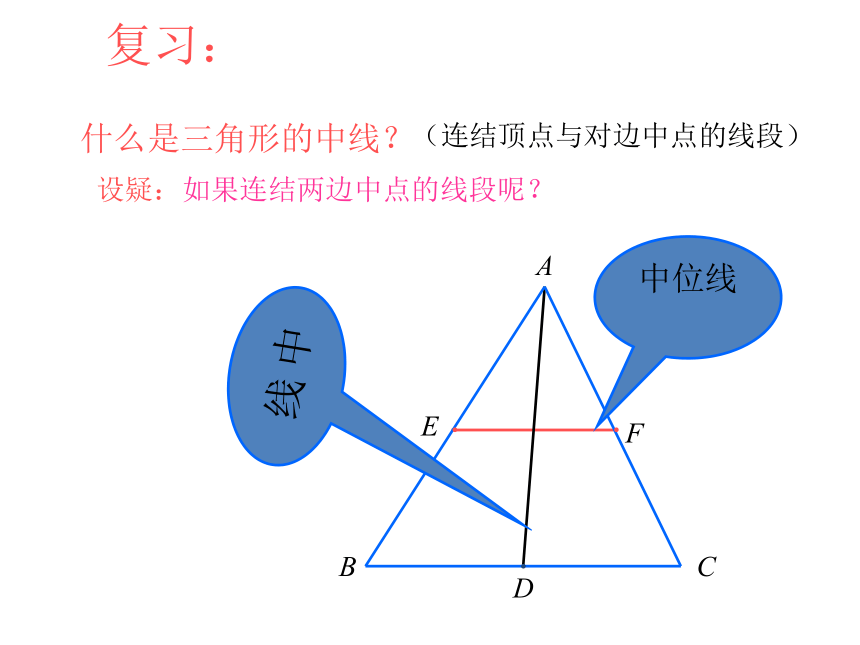
复习:
A
B
C
E
F
.
.
D
.
中位线
中线
什么是三角形的中线?
(连结顶点与对边中点的线段)
设疑:如果连结两边中点的线段呢?
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
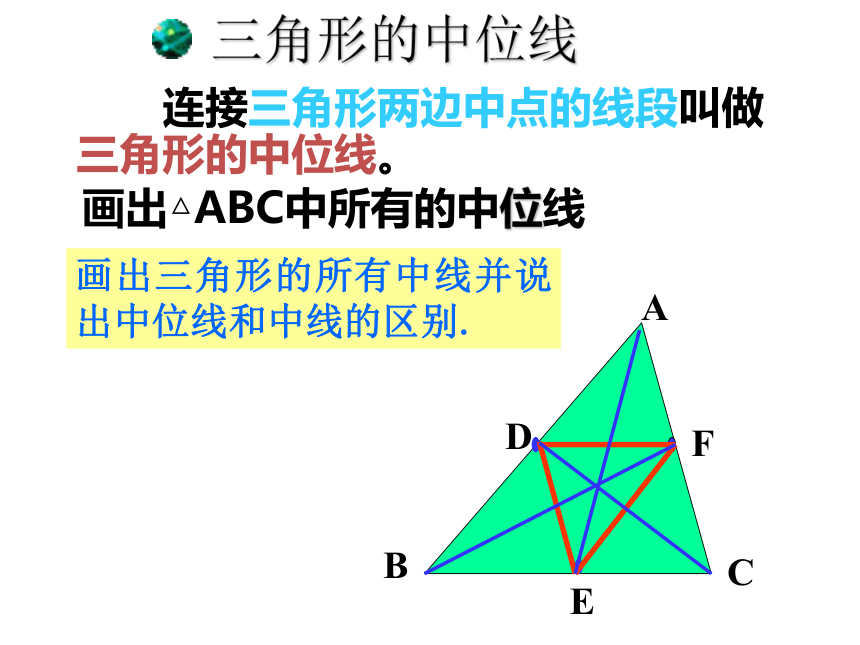
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
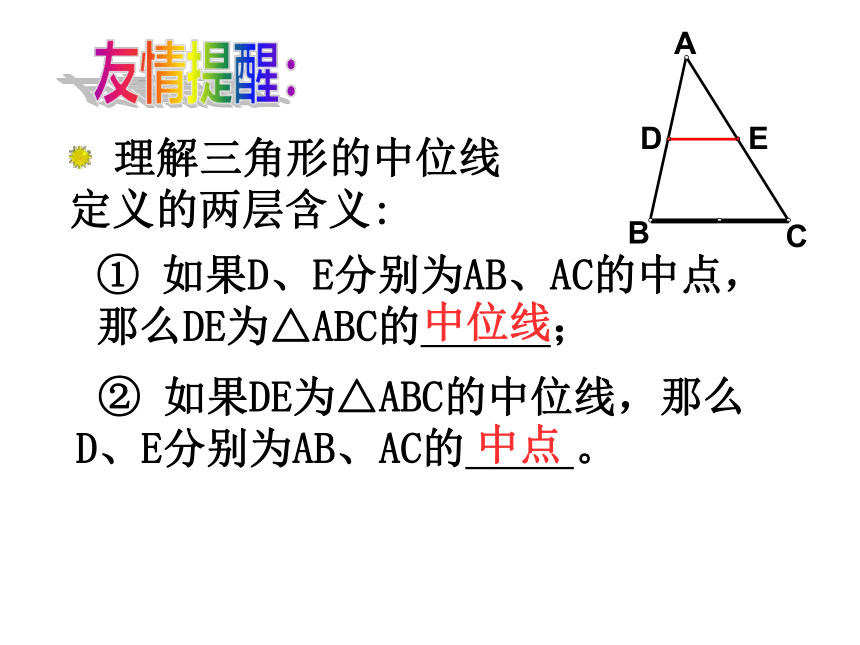
理解三角形的中位线定义的两层含义:
②
如果DE为△ABC的中位线,那么
D、E分别为AB、AC的
。
①
如果D、E分别为AB、AC的中点,
那么DE为△ABC的
;
C
B
A
E
D
中位线
中点
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
A
B
C
D
E
平行
DE是BC的一半
结论:三角形的中位线平行于第三边,并且等于它的一半.
D
A
B
C
E
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE=
BC.
2
1
能说出理由吗?
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE=
BC.
2
1
D
A
B
C
E
F
用不同的方法证明
三角形的中位线的性质
三角形的中位线平行于第三边,并且等于它的一半
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴
DE∥BC,
DE=
BC.
2
1
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B=
度,为什么?
(2)若BC=8cm,
则DE=
cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长=
cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
问题
例1
求证三角形的一条中位线与第三边上的中线互相平分.
已知: 如图24.4.3所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.
证明
连结DE、EF.
∵
AD=DB,BE=EC,
∴
DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴
AE、DF互相平分(平行四边形的对角线互相平分).
例2
如图24.4.4,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
证明
:连结ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴ △ACG∽△DEG,
∴
∴
如果在上图中,取AC的中点F,假设BF与AD交于G`,如下图,那么我们同理有,
所以有
,即两图中的点G与G`是重合的。
于是我们有以下结论:
三角形三条边上的中线交于
一点,这个点就是三形的
重心,重心与一边中点
的连线的长是对应中线长的
A
B
C
D
F
G`
A
G`
数学上的重心与物理上的重心是一致的
1、如图:EF是△ABC
的中位线,BC=20,则EF=
(
)
;
10
2、在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是(
)
平行且相等
求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD
∴HG∥AC,
HG=
AC
同理
EF∥AC
EF=
AC
∴HG∥EF
HG=EF
∴四边形EFGH是平行四边形.
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=36
m,则AB=
2MN=72
m
如果,MN两点之间还有阻隔,你有什么解决办法?
④顺次连结对角线相等且互相垂直的四边形四边中点所得的四边形是—————
一些重要结论:
②顺次连结对角线相等的四边形四边中点所得的四边形是————
③顺次连结对角线互相垂直的四边形四边中点所得的四边形是————
①顺次连结四边形四边中点所得的四边形是———————
平行四边形.
矩形.
菱形.
正方形.
下
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
①顺次连结平行四边形四边中点所得的四边形是————————
②顺次连结等腰梯形四边中点所得的四边形是——————
③顺次连结矩形四边中点所得的四边形是——————
④顺次连结菱形四边中点所得的四边形是——————
⑤顺次连结正方形四边中点所得的四边形是—————
1、填空题:
下
3.已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——,
面积为△ABC面积的——,
2.已知:三角形的各边分别为6cm,8cm,
10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。
6
10
8
3
5
4
B
C
A
D
E
F
∠B
——
∠ADE(填“=”或“≠”)
=
H
P
N
下
4.如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP=
———,BC=
———
3
4.5
9
1.5
P
A
B
F
G
E
C
D
下
BC=CD,则顺次连结它的各边中点得到的四边形是(
)
A
等腰梯形
C
菱形
D
正方形
B
矩形
C
A
B
D
O
E
F
H
G
5.在四边形ABCD中,AB=AD,
6.已知:E为平行四边形ABCD中DC边的延长
线上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证:
AB=
2
OF
A
D
B
C
E
G
F
O
提示:证明△ABF≌
△ECF,
得BF=CF,再证OF是△ABC的中位线.
7.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
学习目标
知识与技能:理解三角形中位线定义与性质,会应用三角形中位线解决实际问题.
过程与方法:经历探究三角形中位线定义、性质的过程,感受三角形中位线定理的应用思想。
情感、态度与价值观:培养良好的探究意识和合作交流的习惯,体会数学推理的应用价值.
实验:请同学们思考:将任意一个三角形分成四个全等的三角形,你是如何切割的?
图中有几个平行四边形?你是如何判断的?
(答案如图)
怎样将一张三角形硬纸片剪成两部分,使分成的两部分能拼成一个平行四边形?
请动手试一试!
复习:
A
B
C
E
F
.
.
D
.
中位线
中线
什么是三角形的中线?
(连结顶点与对边中点的线段)
设疑:如果连结两边中点的线段呢?
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
三角形的中位线
连接三角形两边中点的线段叫做三角形的中位线。
A
B
C
画出△ABC中所有的中位线
画出三角形的所有中线并说出中位线和中线的区别.
D
E
F
理解三角形的中位线定义的两层含义:
②
如果DE为△ABC的中位线,那么
D、E分别为AB、AC的
。
①
如果D、E分别为AB、AC的中点,
那么DE为△ABC的
;
C
B
A
E
D
中位线
中点
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
A
B
C
D
E
平行
DE是BC的一半
结论:三角形的中位线平行于第三边,并且等于它的一半.
D
A
B
C
E
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE=
BC.
2
1
能说出理由吗?
如图:在△ABC中,D是AB的中点,E是AC的中点。
则有:
DE∥BC,
DE=
BC.
2
1
D
A
B
C
E
F
用不同的方法证明
三角形的中位线的性质
三角形的中位线平行于第三边,并且等于它的一半
用符号语言表示
D
A
B
C
E
∵DE是△ABC的中位线
∴
DE∥BC,
DE=
BC.
2
1
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B=
度,为什么?
(2)若BC=8cm,
则DE=
cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长=
cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
问题
例1
求证三角形的一条中位线与第三边上的中线互相平分.
已知: 如图24.4.3所示,在△ABC中,AD=DB,BE=EC,AF=FC.
求证: AE、DF互相平分.
证明
连结DE、EF.
∵
AD=DB,BE=EC,
∴
DE∥AC(三角形的中位线平行于第三边并且等于第三边的一半).
同理EF∥AB.
∴四边形ADEF是平行四边形.
∴
AE、DF互相平分(平行四边形的对角线互相平分).
例2
如图24.4.4,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
证明
:连结ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC,
(三角形的中位线平行于第三边并且等于第三边的一半),
∴ △ACG∽△DEG,
∴
∴
如果在上图中,取AC的中点F,假设BF与AD交于G`,如下图,那么我们同理有,
所以有
,即两图中的点G与G`是重合的。
于是我们有以下结论:
三角形三条边上的中线交于
一点,这个点就是三形的
重心,重心与一边中点
的连线的长是对应中线长的
A
B
C
D
F
G`
A
G`
数学上的重心与物理上的重心是一致的
1、如图:EF是△ABC
的中位线,BC=20,则EF=
(
)
;
10
2、在△ABC中,中线CE、BF相交点O、M、N分别是OB、OC的中点,则EF和MN的关系是(
)
平行且相等
求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
求证:顺次连结四边形四条边的中点所得的四边形是平行四边形。
已知:在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
证明:连结AC.
∵AH=HD,CG=GD
∴HG∥AC,
HG=
AC
同理
EF∥AC
EF=
AC
∴HG∥EF
HG=EF
∴四边形EFGH是平行四边形.
A
B
C
测出MN的长,就可知A、B两点的距离
M
N
在AB外选一点C,使C能直接到达A和B,
连结AC和BC,并分别找出AC和BC的中点M、N.
若MN=36
m,则AB=
2MN=72
m
如果,MN两点之间还有阻隔,你有什么解决办法?
④顺次连结对角线相等且互相垂直的四边形四边中点所得的四边形是—————
一些重要结论:
②顺次连结对角线相等的四边形四边中点所得的四边形是————
③顺次连结对角线互相垂直的四边形四边中点所得的四边形是————
①顺次连结四边形四边中点所得的四边形是———————
平行四边形.
矩形.
菱形.
正方形.
下
1.三角形的中位线定义.
2.三角形的中位线定理.
3.三角形的中位线定理不仅给出了中位线与第三边的关系,而且给出了他们的数量关系,在三角形中给出一边的中点时,要转化为中位线.
4.线段的倍分要转化为相等问题来解决.
5.三角形的中位线定理的发现过程所用到的数学方法(包括画图、实验、猜想、分析、归纳等.)
①顺次连结平行四边形四边中点所得的四边形是————————
②顺次连结等腰梯形四边中点所得的四边形是——————
③顺次连结矩形四边中点所得的四边形是——————
④顺次连结菱形四边中点所得的四边形是——————
⑤顺次连结正方形四边中点所得的四边形是—————
1、填空题:
下
3.已知:△ABC三边长分别为a,b,c,它的三条中位线组成△DEF,△DEF的三条中位线又组成△HPN,则△HPN的周长等于——————,为△ABC周长的——,
面积为△ABC面积的——,
2.已知:三角形的各边分别为6cm,8cm,
10cm,则连结各边中点所成三角形的周长为——cm,面积为——cm2,为原三角形面积的——。
6
10
8
3
5
4
B
C
A
D
E
F
∠B
——
∠ADE(填“=”或“≠”)
=
H
P
N
下
4.如图,AF=FD=DB,FG∥DE∥BC,PE=1.5,则DP=
———,BC=
———
3
4.5
9
1.5
P
A
B
F
G
E
C
D
下
BC=CD,则顺次连结它的各边中点得到的四边形是(
)
A
等腰梯形
C
菱形
D
正方形
B
矩形
C
A
B
D
O
E
F
H
G
5.在四边形ABCD中,AB=AD,
6.已知:E为平行四边形ABCD中DC边的延长
线上一点,且CE=DC,连结AE,分别交BC、BD于
点F、G,连接AC交BD于O,连结OF.
求证:
AB=
2
OF
A
D
B
C
E
G
F
O
提示:证明△ABF≌
△ECF,
得BF=CF,再证OF是△ABC的中位线.
7.已知:如图,E、F、G、H分别是AB、BC、CD、DA的中点.求证:四边形EFGH是平行四边形.
