鲁教版五四小学六年级上册数学 第四章达标检测卷(Word版含答案)
文档属性
| 名称 | 鲁教版五四小学六年级上册数学 第四章达标检测卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览


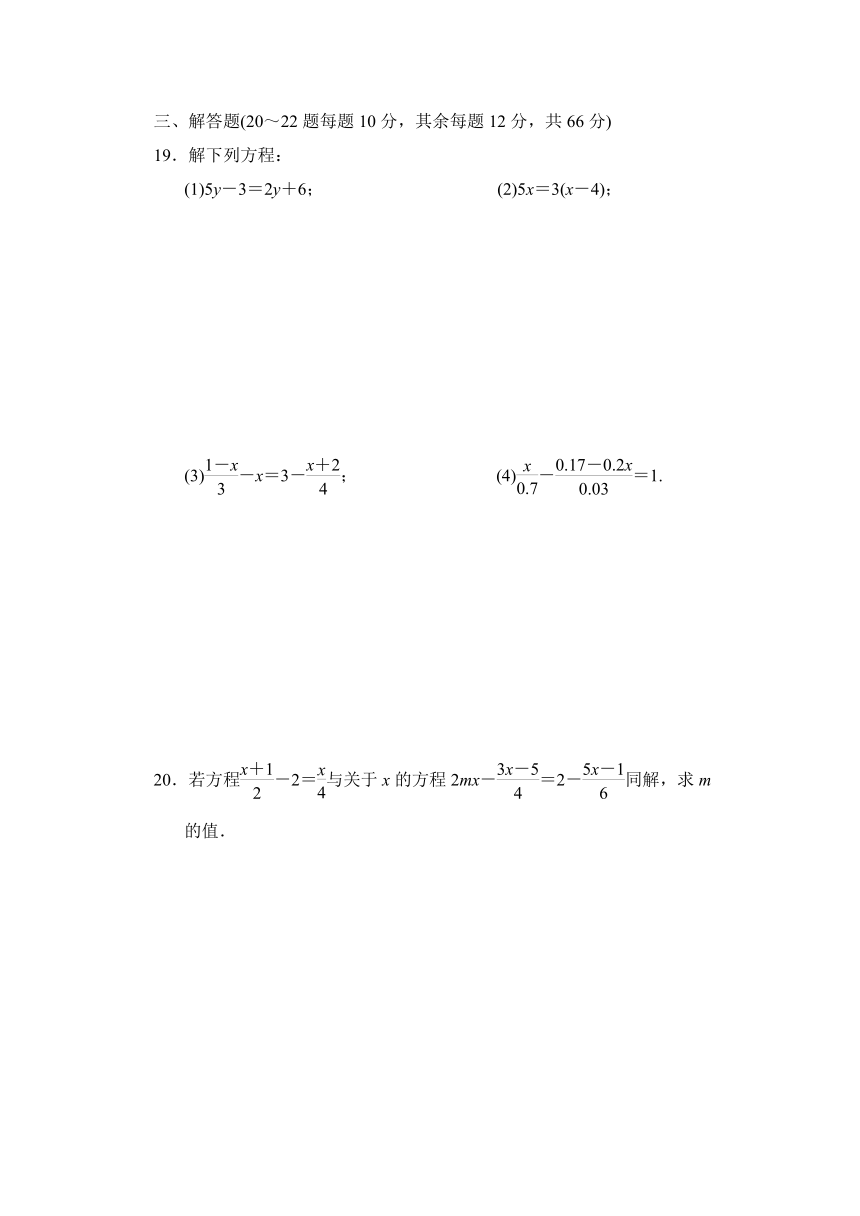

文档简介
第四章达标检测卷
一、选择题(每题3分,共30分)
1.下列等式是一元一次方程的是( )
A.x-2=3
B.1+5=6
C.x2+x=1
D.x-3y=0
2.下列等式变形正确的是( )
A.若a=b,则a-3=3-b
B.若x=y,则=
C.若a=b,则ac=bc
D.若=,则b=d
3.下列四组变形中,属于移项变形的是( )
A.由5x+10=0,得5x=-10
B.由=4,得x=12
C.由3y=-4,得y=-
D.由2x-(3-x)=6,得2x-3+x=6
4.将方程+1=去分母后正确的是( )
A.3(x+2)+1=4x
B.12(x+2)+12=12x
C.4(x+2)+12=3x
D.3(x+2)+12=4x
5.若2(a+3)的值与4互为相反数,则a的值为( )
A.-1
B.-
C.-5
D.
6.若x=-3是方程2(x-m)=6的解,则m的值为( )
A.6
B.-6
C.12
D.-12
7.已知方程7x+2=3x-6与关于x的方程x-1=k的解相同,则3k2-1的值为( )
A.18
B.20
C.26
D.-26
8.甲、乙两人练习赛跑,甲每秒跑7
m,乙每秒跑6.5
m,甲让乙先跑5
m,设甲跑x
s后可追上乙,则下列四个方程中不正确的是( )
A.7x=6.5x+5
B.7x+5=6.5x
C.(7-6.5)x=5
D.6.5x=7x-5
9.小马虎在做作业,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1
B.2
C.3
D.4
10.已知a为整数,关于x的一元一次方程2x+1=+3的解也为整数,则所有满足条件的数a的和为( )
A.0
B.24
C.36
D.48
二、填空题(每题3分,共24分)
11.方程(m+1)x|m|-2=1是关于x的一元一次方程,则m=________.
12.已知x=3是关于x的方程a(x-1)=3x-5的解,那么a的值等于________.
13.如图有三个平衡的天平,请问第三个天平“?”处放________个.
14.美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量比国画作品数量的2倍多7幅,则展出的油画作品有________幅.
15.一个两位数,个位上的数字是十位上的数字的2倍,如果把十位上与个位上的数字对调,那么所得的两位数比原两位数大27,求原两位数.若设原两位数个位上的数字为x,则可列方程为____________________;若设原两位数十位上的数字为y,则可列方程为______________________.
16.甲、乙两个足球队连续进行对抗赛,规定胜一场得3分,平一场得1分,负一场得0分,共赛10场,甲队保持不败,得22分,甲队胜_______场.
17.
一台空调标价2
000元,若按六折销售仍可获利20%,则这台空调的进价是________元.
18.如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55
cm,此时木桶中水的深度是________.
三、解答题(20~22题每题10分,其余每题12分,共66分)
19.解下列方程:
(1)5y-3=2y+6; (2)5x=3(x-4);
(3)-x=3-;
(4)-=1.
20.若方程-2=与关于x的方程2mx-=2-同解,求m
的值.
21.下面是小红解方程-=1的过程.
解:去分母,得2(2x+1)-5x-1=1.①
去括号,得4x+2-5x-1=1.②
移项,得4x-5x=1-2+1.③
合并同类项,得-x=0.④
系数化为1,得x=0.⑤
上述解方程的过程中,是否有错误?
答:________(填“有”或者“没有”);如果有错误,则开始出错的一步是________(填序号).如果上述解方程有错误,请你给出正确的解题过程.
22.《计算之书》是意大利中世纪著名数学家斐波那契(公元1175—1250年)的经典之作.书中记载了一道非常有趣的“狐跑犬追”问题:在相同的时间里,猎犬每跑9
m,狐狸跑6
m.若狐狸与猎犬同时起跑时狐狸在猎犬前面50
m,问狐狸跑多少米后被猎犬追上?
23.某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
(2)已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3
950元.则甲、乙两车每天的租金分别为多少元?
24.元旦期间,各大商场纷纷推出优惠政策吸引顾客,下面是百盛和武商两个商场各自推出的优惠办法:
百盛:1.若一次购物不超过500元,不予优惠.2.若一次购物超过500元,但不超过1
000元,所有商品享受9折优惠.3.若一次购物超过1
000元,不超过1
000元的部分享受九折优惠,超过1
000元的部分享受6折优惠;
武商:1.若一次购物不超过500元,不予优惠.2.若一次购物超过500元,则所有商品享受8折优惠.
(1)王老师想到百盛买件标价为1
800元的衣服,她应该付多少钱?
(2)请问当我们购买多少钱的商品时,在两个商场所花的钱相同?
(3)王老师元旦打算消费3
000元购买自己想要的商品,她有三种打算:①到百盛和武商各消费1
500元;②全到百盛去消费;③全到武商去消费.假设王老师需要的商品百盛和武商都有,如果你是王老师,你会如何选择?
答案
一、1.A 2.C 3.A 4.D 5.C 6.B 7.C 8.B 9.B
10.D 点拨:因为2x+1=+3,所以(6-a)x=6,因为关于x的一元一次方程2x+1=+3的解为整数,所以x=为整数,又因为a为整数,所以6-a=±1或±2或±3或±6,所以a=5或7或4或8或3或9或0或12,所以所有满足条件的数a的和为5+7+4+8+3+9+0+12=48.
二、11.1 12.2
13.5 点拨:由第一个天平可知:=+,将第二个天平中的换作+,可得+=++,即=+,将第一个天平中的换作+,可得=++,因此,+=++++,即第三个天平“?”处放5个.
14.69
15.10×+x=10x+-27;
10y+2y=10×2y+y-27
16.6 17.1
000 18.20
cm
三、19.解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得5x=3x-12.
移项,得5x-3x=-12.
合并同类项,得2x=-12.
系数化为1,得x=-6.
(3)去分母,得4(1-x)-12x=36-3(x+2).
去括号,得4-4x-12x=36-3x-6.
移项,得3x-4x-12x=36-6-4.
合并同类项,得-13x=26.
系数化为1,得x=-2.
(4)原方程可化为-=1.
去分母,得30x-7(17-20x)=21.
去括号,得30x-119+140x=21.
移项、合并同类项,得170x=140.
系数化为1,得x=.
20.解:解方程-2=,得x=6,
将x=6代入2mx-=2-中,
得12m-=2-,
解得m=.
21.解:有;①
正确的解题过程:
去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项,得4x-5x=6-2-1.
合并同类项,得-x=3.
系数化为1,得x=-3.
22.解:设狐狸跑x
m后被猎犬追上,此时猎犬跑了x
m,
依题意,得x-x=50,解得x=100.
答:狐狸跑100
m后被猎犬追上.
23.解:(1)设甲、乙两车合作还需要x天运完垃圾,
依题意,得+=1,解得x=8.
答:甲、乙两车合作还需要8天运完垃圾.
(2)设乙车每天的租金为y元,则甲车每天的租金为(y+100)元,
依题意,得:(8+3)(y+100)+8y=3
950,解得:y=150,所以y+100=250.
答:甲车每天的租金为250元,乙车每天的租金为150元.
24.解:(1)1
000×0.9+(1
800-1
000)×0.6=1
380(元).
答:她应该付1
380元钱.
(2)一次购物不超过500元,在两个商场都不享受优惠;
一次购物超过1
000元,设当我们购买x元钱的商品时,在两个商场所花的钱相同,依题意有
1
000×0.9+0.6(x-1
000)=0.8x,解得x=1
500.
综上所述,当我们购买不超过500元钱或1
500元钱的商品时,在两个商场所花的钱相同;
(3)①1
000+(1
500-1
000×0.9)÷0.6=2
000(元),
1
500÷0.8=1
875(元),
2
000+1
875=3
875(元);
②1
000+(3
000-1
000×0.9)÷0.6=4
500(元);
③3
000÷0.8=3
750(元);
因为4
500>3
875>3
750,
所以选择第②种打算.
一、选择题(每题3分,共30分)
1.下列等式是一元一次方程的是( )
A.x-2=3
B.1+5=6
C.x2+x=1
D.x-3y=0
2.下列等式变形正确的是( )
A.若a=b,则a-3=3-b
B.若x=y,则=
C.若a=b,则ac=bc
D.若=,则b=d
3.下列四组变形中,属于移项变形的是( )
A.由5x+10=0,得5x=-10
B.由=4,得x=12
C.由3y=-4,得y=-
D.由2x-(3-x)=6,得2x-3+x=6
4.将方程+1=去分母后正确的是( )
A.3(x+2)+1=4x
B.12(x+2)+12=12x
C.4(x+2)+12=3x
D.3(x+2)+12=4x
5.若2(a+3)的值与4互为相反数,则a的值为( )
A.-1
B.-
C.-5
D.
6.若x=-3是方程2(x-m)=6的解,则m的值为( )
A.6
B.-6
C.12
D.-12
7.已知方程7x+2=3x-6与关于x的方程x-1=k的解相同,则3k2-1的值为( )
A.18
B.20
C.26
D.-26
8.甲、乙两人练习赛跑,甲每秒跑7
m,乙每秒跑6.5
m,甲让乙先跑5
m,设甲跑x
s后可追上乙,则下列四个方程中不正确的是( )
A.7x=6.5x+5
B.7x+5=6.5x
C.(7-6.5)x=5
D.6.5x=7x-5
9.小马虎在做作业,不小心将方程中的一个常数污染了,被污染的方程是2(x-3)-■=x+1,怎么办呢?他想了想便翻看书后的答案,方程的解是x=9,请问这个被污染的常数是( )
A.1
B.2
C.3
D.4
10.已知a为整数,关于x的一元一次方程2x+1=+3的解也为整数,则所有满足条件的数a的和为( )
A.0
B.24
C.36
D.48
二、填空题(每题3分,共24分)
11.方程(m+1)x|m|-2=1是关于x的一元一次方程,则m=________.
12.已知x=3是关于x的方程a(x-1)=3x-5的解,那么a的值等于________.
13.如图有三个平衡的天平,请问第三个天平“?”处放________个.
14.美术馆举办的一次画展中,展出的油画作品和国画作品共有100幅,其中油画作品数量比国画作品数量的2倍多7幅,则展出的油画作品有________幅.
15.一个两位数,个位上的数字是十位上的数字的2倍,如果把十位上与个位上的数字对调,那么所得的两位数比原两位数大27,求原两位数.若设原两位数个位上的数字为x,则可列方程为____________________;若设原两位数十位上的数字为y,则可列方程为______________________.
16.甲、乙两个足球队连续进行对抗赛,规定胜一场得3分,平一场得1分,负一场得0分,共赛10场,甲队保持不败,得22分,甲队胜_______场.
17.
一台空调标价2
000元,若按六折销售仍可获利20%,则这台空调的进价是________元.
18.如图,两根铁棒直立于桶底水平的木桶中,在木桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为55
cm,此时木桶中水的深度是________.
三、解答题(20~22题每题10分,其余每题12分,共66分)
19.解下列方程:
(1)5y-3=2y+6; (2)5x=3(x-4);
(3)-x=3-;
(4)-=1.
20.若方程-2=与关于x的方程2mx-=2-同解,求m
的值.
21.下面是小红解方程-=1的过程.
解:去分母,得2(2x+1)-5x-1=1.①
去括号,得4x+2-5x-1=1.②
移项,得4x-5x=1-2+1.③
合并同类项,得-x=0.④
系数化为1,得x=0.⑤
上述解方程的过程中,是否有错误?
答:________(填“有”或者“没有”);如果有错误,则开始出错的一步是________(填序号).如果上述解方程有错误,请你给出正确的解题过程.
22.《计算之书》是意大利中世纪著名数学家斐波那契(公元1175—1250年)的经典之作.书中记载了一道非常有趣的“狐跑犬追”问题:在相同的时间里,猎犬每跑9
m,狐狸跑6
m.若狐狸与猎犬同时起跑时狐狸在猎犬前面50
m,问狐狸跑多少米后被猎犬追上?
23.某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
(2)已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3
950元.则甲、乙两车每天的租金分别为多少元?
24.元旦期间,各大商场纷纷推出优惠政策吸引顾客,下面是百盛和武商两个商场各自推出的优惠办法:
百盛:1.若一次购物不超过500元,不予优惠.2.若一次购物超过500元,但不超过1
000元,所有商品享受9折优惠.3.若一次购物超过1
000元,不超过1
000元的部分享受九折优惠,超过1
000元的部分享受6折优惠;
武商:1.若一次购物不超过500元,不予优惠.2.若一次购物超过500元,则所有商品享受8折优惠.
(1)王老师想到百盛买件标价为1
800元的衣服,她应该付多少钱?
(2)请问当我们购买多少钱的商品时,在两个商场所花的钱相同?
(3)王老师元旦打算消费3
000元购买自己想要的商品,她有三种打算:①到百盛和武商各消费1
500元;②全到百盛去消费;③全到武商去消费.假设王老师需要的商品百盛和武商都有,如果你是王老师,你会如何选择?
答案
一、1.A 2.C 3.A 4.D 5.C 6.B 7.C 8.B 9.B
10.D 点拨:因为2x+1=+3,所以(6-a)x=6,因为关于x的一元一次方程2x+1=+3的解为整数,所以x=为整数,又因为a为整数,所以6-a=±1或±2或±3或±6,所以a=5或7或4或8或3或9或0或12,所以所有满足条件的数a的和为5+7+4+8+3+9+0+12=48.
二、11.1 12.2
13.5 点拨:由第一个天平可知:=+,将第二个天平中的换作+,可得+=++,即=+,将第一个天平中的换作+,可得=++,因此,+=++++,即第三个天平“?”处放5个.
14.69
15.10×+x=10x+-27;
10y+2y=10×2y+y-27
16.6 17.1
000 18.20
cm
三、19.解:(1)移项,得5y-2y=6+3.
合并同类项,得3y=9.
系数化为1,得y=3.
(2)去括号,得5x=3x-12.
移项,得5x-3x=-12.
合并同类项,得2x=-12.
系数化为1,得x=-6.
(3)去分母,得4(1-x)-12x=36-3(x+2).
去括号,得4-4x-12x=36-3x-6.
移项,得3x-4x-12x=36-6-4.
合并同类项,得-13x=26.
系数化为1,得x=-2.
(4)原方程可化为-=1.
去分母,得30x-7(17-20x)=21.
去括号,得30x-119+140x=21.
移项、合并同类项,得170x=140.
系数化为1,得x=.
20.解:解方程-2=,得x=6,
将x=6代入2mx-=2-中,
得12m-=2-,
解得m=.
21.解:有;①
正确的解题过程:
去分母,得2(2x+1)-(5x-1)=6.
去括号,得4x+2-5x+1=6.
移项,得4x-5x=6-2-1.
合并同类项,得-x=3.
系数化为1,得x=-3.
22.解:设狐狸跑x
m后被猎犬追上,此时猎犬跑了x
m,
依题意,得x-x=50,解得x=100.
答:狐狸跑100
m后被猎犬追上.
23.解:(1)设甲、乙两车合作还需要x天运完垃圾,
依题意,得+=1,解得x=8.
答:甲、乙两车合作还需要8天运完垃圾.
(2)设乙车每天的租金为y元,则甲车每天的租金为(y+100)元,
依题意,得:(8+3)(y+100)+8y=3
950,解得:y=150,所以y+100=250.
答:甲车每天的租金为250元,乙车每天的租金为150元.
24.解:(1)1
000×0.9+(1
800-1
000)×0.6=1
380(元).
答:她应该付1
380元钱.
(2)一次购物不超过500元,在两个商场都不享受优惠;
一次购物超过1
000元,设当我们购买x元钱的商品时,在两个商场所花的钱相同,依题意有
1
000×0.9+0.6(x-1
000)=0.8x,解得x=1
500.
综上所述,当我们购买不超过500元钱或1
500元钱的商品时,在两个商场所花的钱相同;
(3)①1
000+(1
500-1
000×0.9)÷0.6=2
000(元),
1
500÷0.8=1
875(元),
2
000+1
875=3
875(元);
②1
000+(3
000-1
000×0.9)÷0.6=4
500(元);
③3
000÷0.8=3
750(元);
因为4
500>3
875>3
750,
所以选择第②种打算.
