7.1 植树问题(一) 人教版(33张PPT)
文档属性
| 名称 | 7.1 植树问题(一) 人教版(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-31 21:30:22 | ||
图片预览







文档简介
(共33张PPT)
第
1
课时
植树问题(一)
7
数学广角——植树问题
R
五年级上册
课后作业
探索新知
课堂小结
当堂检测
(1)不封闭路段两端都植树的问题
(2)不封闭路段两端都不植树的问题
(3)不封闭路段一端植树一端不植树的问题
1
课堂探究点
2
课时流程
探究点
1
不封闭路段两端都植树的问题
例1:同学们在全长100
m的小路一边植树,每隔5
m栽
一棵(两端要栽)。一共要栽多少棵树?
1.
你都知道了什么?怎么理解“两端都栽”?
2.
你认为一共要栽多少棵树?
到底一共要栽多少棵树呢,你能想办法验证一下吗?
我们可以以20米、25米为例进行研究,我们可以用什么方法?
提示:
1.我们把100米叫做“总长”。
2.把5米叫做“间隔距离”。
3.我们通常把树与树之间叫做“间隔”。
当遇到较为复杂的数学问题时,可以先从简单的事例中发现规律,然后应用找到的规律解决原来的问题。
每隔5
m栽一棵,共
栽100÷5=20(棵)。
总长(m)
间隔距离(m)
间隔数(个)
棵数(棵)
5
5
10
20
25
30
60
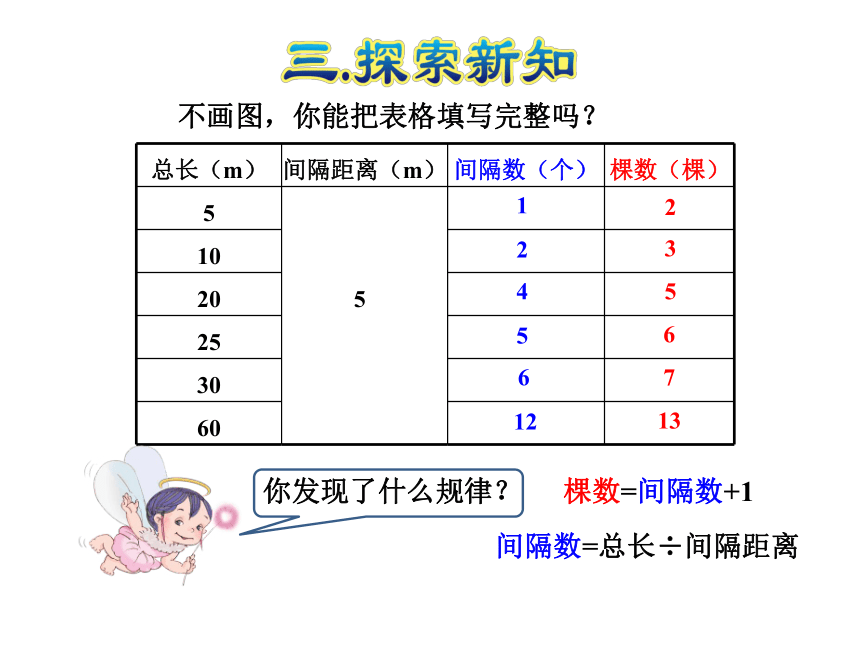
不画图,你能把表格填写完整吗?
你发现了什么规律?
棵数=间隔数+1
1
2
2
3
4
5
5
6
6
7
12
13
间隔数=总长÷间隔距离
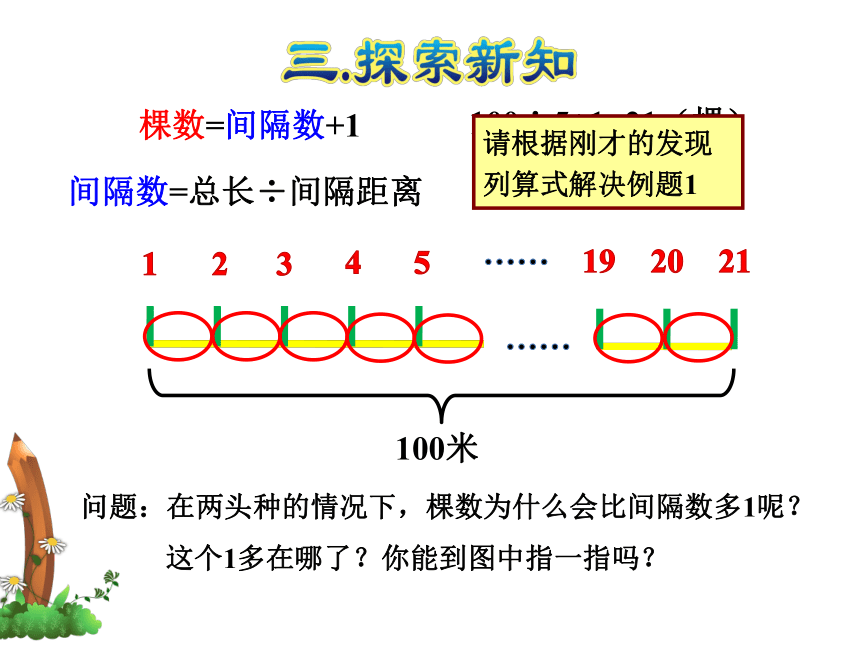
问题:在两头种的情况下,棵数为什么会比间隔数多1呢?
这个1多在哪了?你能到图中指一指吗?
100米
棵数=间隔数+1
100÷5+1=21(棵)
间隔数
棵数
+1=
间隔数=总长÷间隔距离
请根据刚才的发现列算式解决例题1
归纳总结:
在一条线段上植树,两端都栽的情况:
间隔数=总长÷间隔距离
棵数=间隔数+1
小试牛刀
5路公共汽车行驶路线全长12
km,相邻两站之间的路程都是1
km。一共设有多少个车站?
(选题源于教材P109第2题)
12
÷1=12(个)
12+1=13(个)
答:一共设有13个车站。
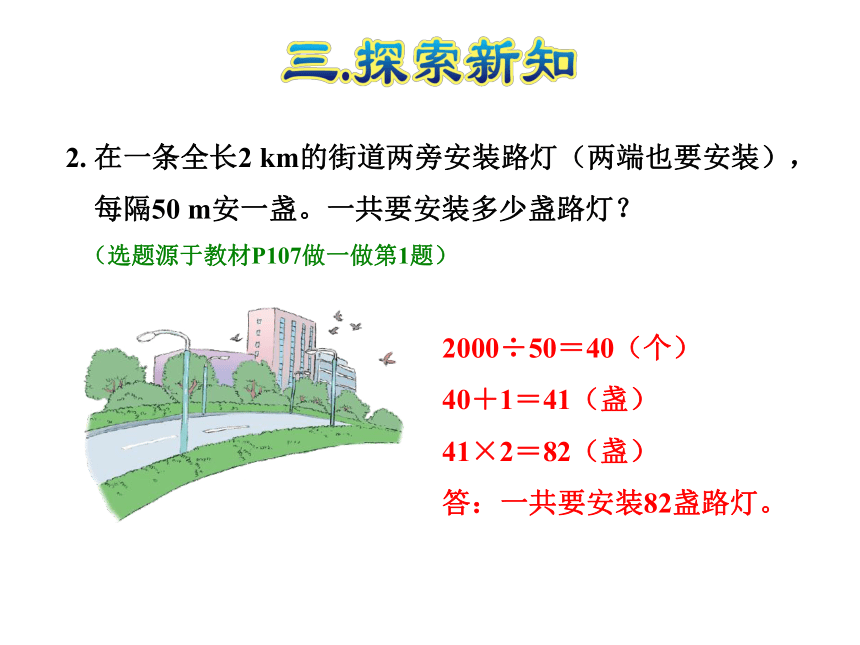
2.
在一条全长2
km的街道两旁安装路灯(两端也要安装),
每隔50
m安一盏。一共要安装多少盏路灯?
(选题源于教材P107做一做第1题)
2000÷50=40(个)
40+1=41(盏)
41×2=82(盏)
答:一共要安装82盏路灯。
3.
园林工人沿一条笔直的公路一侧植树,每隔6
m
种一棵,一共种了36棵。从第一棵到最后一棵
的距离有多远?(选题源于教材P109第4题)
36-1=35(个)
35×6=210(米)
答:从第一棵到最后一棵的距离有210米。
探究点
2
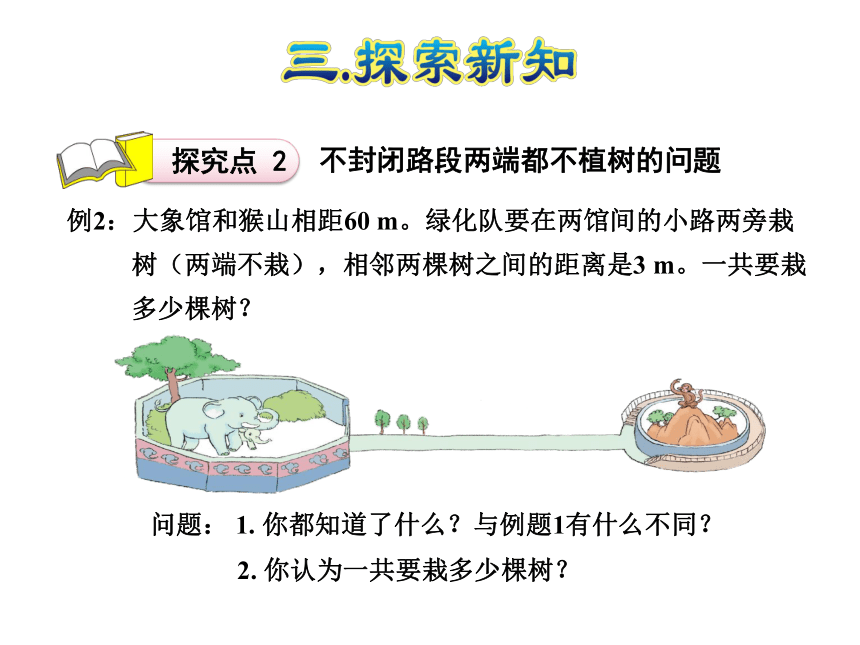
不封闭路段两端都不植树的问题
问题:
1.
你都知道了什么?与例题1有什么不同?
2.
你认为一共要栽多少棵树?
例2:大象馆和猴山相距60
m。绿化队要在两馆间的小路两旁栽
树(两端不栽),相邻两棵树之间的距离是3
m。一共要栽
多少棵树?
自学提示:
1.请根据学习例题1的经验,先自主研究。
2.自主探索之后,先与同桌交流,然后在小组内交流。
3.将自己研究的成果,归纳总结出规律用式子去表示。
间隔数=总长÷间隔距离
棵数=间隔数-1
60÷3=20(个)
20-1=19(棵)
19×2
=38(棵)
1.为什么要用20减1呢?减的1你能说一说是在哪里吗?
2.为什么最后用19乘2?
问题:
1.
在两头都不种的情况下,棵数为什么会比间
隔数少1呢?
2.
少的“1”在哪呢,请你到图中指一指。
60米
棵数=间隔数-1
问题:
1.
比较两种情况,有什么相同?有什么不同?
2.
如果你忘记结论,可以怎样做呢?
棵数=间隔数+1
棵数=间隔数-1
100米
60米
两头种
两头不种
归纳总结:
在一条线段上植树(两端都不栽)的情况:
间隔数=总长÷间隔距离
棵数=间隔数-1
小试牛刀
1.
一条走廊长32
m,每隔4
m摆放一盆植物(两端不放)。
一共要放多少盆植物?
(选题源于教材P109第6题)
32÷4=8(个)
8-1=7(盆)
答:一共要放7盆植物。
5-1=4(次)
4×8=32(分钟)
答:锯完一共要花32分钟。
2.
一根木头长10m,要把它平均分成5段。每锯下一段需要
8分钟。锯完一共要花多少分钟?(选题源于教材P110第8题)
锯木头时,锯成n段,需要锯(n-1)次,锯每次的时间与次数相乘就是所需时间。
探究点
3
不封闭路段一端植树一端不植树的问题
例3:小明家门前有一条35
m的小路,绿化队要在路旁栽一
排树。每隔5
m栽一棵树(一端栽一端不栽)。一共
要栽多少棵?
该怎样列式计算呢?试一试吧!
35÷5=7(棵)
答:一共要栽7棵树。
为什么间隔数等于棵树?请用图示加以说明。
问题:1.
植树问题有哪几种情况?
每种情况中棵数与间隔数之间是什么关系?
2.
我们是通过什么方法得到这些结论的?
3.
如果你忘记或者混淆了这些情况,可以怎样做?
棵数=间隔数+1
100米
35米
两头种
60米
两头不种
棵数=间隔数-1
一头种
棵数=间隔数
间隔数=总长÷间隔距离
棵数=间隔数
归纳总结:
在一条线段上植树(一端栽,一端不栽)的情况:
42÷3=14(处)
答:全程一共有14处这样的服务点。
1.
马拉松比赛全程约42
km。平均每3
km设置一处饮水服务点
(起点不设,终点设),全程一共有多少处这样的服务点?
(选题源于教材P110第7题)
小试牛刀
两端都栽
棵数=间隔数+1
两端不栽
棵数=间隔数-1
一端栽一端不栽
棵树=间隔数
间隔数=总长÷间隔距离
植树问题基本解决思路:
1.要在学校门口一条长180
m的林荫路的一侧栽树,起点和终点都栽。如果每相邻两棵树之间的距离是3
m,需要多少棵树?
夯实基础
180÷3+1=61(棵)
答:需要61棵树。
2.在一条长40
m的小路两旁,每隔2
m栽一棵树(两端都栽),一共要栽多少棵树?
(40÷2+1)×2=42(棵)
答:一共要栽42棵树。
3.两根电线杆相距200
m,在两根电线杆之间每隔5
m栽一棵树(两端都不栽),一共可以栽多少棵树?
200÷5-1=39(棵)
答:一共要栽39棵树。
4.在绿化工程中,要在公园和动物园之间的马路两旁栽树(两端都不栽),每相邻两棵树之间相距4米,一共要栽多少棵树?
(400÷4-1)×2=198(棵)
答:一共要栽198棵树。
5.填一填。
学校有一条长为60
m的小道,计划在道路一旁栽树,每隔3
m栽一棵。
想:小道长( )m,每隔( )m栽一棵,有( )个间隔。
(1)如果两端都要栽树,那么一共要栽( )棵树。
(2)如果两端都不栽树,那么一共要栽( )棵树。
60
19
21
20
3
6.在150米长的直跑道的一旁每隔5米插一面彩旗(两端都要插),可以插多少面彩旗?
150÷5+1=31(面)
答:可以插31面彩旗。
7.某大桥的长为4500
m,在桥的两旁每隔45
m装一块广告牌(一端安装,一端不安装),这座大桥一共可以安装多少块广告牌?
4500÷45×2=200(块)
答:一共可以安装200块广告牌。
8.在一条长60米的村级小路两旁每隔5米栽一棵树苗,两端都栽,一共要准备多少棵树苗?
(60÷5+1)×2=26(棵)
答:一共要准备26棵树苗。
易错辨析
辨析:(60÷5+1)算出来的是一侧植树多少棵,在两侧植树时要乘以2。
第
1
课时
植树问题(一)
7
数学广角——植树问题
R
五年级上册
课后作业
探索新知
课堂小结
当堂检测
(1)不封闭路段两端都植树的问题
(2)不封闭路段两端都不植树的问题
(3)不封闭路段一端植树一端不植树的问题
1
课堂探究点
2
课时流程
探究点
1
不封闭路段两端都植树的问题
例1:同学们在全长100
m的小路一边植树,每隔5
m栽
一棵(两端要栽)。一共要栽多少棵树?
1.
你都知道了什么?怎么理解“两端都栽”?
2.
你认为一共要栽多少棵树?
到底一共要栽多少棵树呢,你能想办法验证一下吗?
我们可以以20米、25米为例进行研究,我们可以用什么方法?
提示:
1.我们把100米叫做“总长”。
2.把5米叫做“间隔距离”。
3.我们通常把树与树之间叫做“间隔”。
当遇到较为复杂的数学问题时,可以先从简单的事例中发现规律,然后应用找到的规律解决原来的问题。
每隔5
m栽一棵,共
栽100÷5=20(棵)。
总长(m)
间隔距离(m)
间隔数(个)
棵数(棵)
5
5
10
20
25
30
60
不画图,你能把表格填写完整吗?
你发现了什么规律?
棵数=间隔数+1
1
2
2
3
4
5
5
6
6
7
12
13
间隔数=总长÷间隔距离
问题:在两头种的情况下,棵数为什么会比间隔数多1呢?
这个1多在哪了?你能到图中指一指吗?
100米
棵数=间隔数+1
100÷5+1=21(棵)
间隔数
棵数
+1=
间隔数=总长÷间隔距离
请根据刚才的发现列算式解决例题1
归纳总结:
在一条线段上植树,两端都栽的情况:
间隔数=总长÷间隔距离
棵数=间隔数+1
小试牛刀
5路公共汽车行驶路线全长12
km,相邻两站之间的路程都是1
km。一共设有多少个车站?
(选题源于教材P109第2题)
12
÷1=12(个)
12+1=13(个)
答:一共设有13个车站。
2.
在一条全长2
km的街道两旁安装路灯(两端也要安装),
每隔50
m安一盏。一共要安装多少盏路灯?
(选题源于教材P107做一做第1题)
2000÷50=40(个)
40+1=41(盏)
41×2=82(盏)
答:一共要安装82盏路灯。
3.
园林工人沿一条笔直的公路一侧植树,每隔6
m
种一棵,一共种了36棵。从第一棵到最后一棵
的距离有多远?(选题源于教材P109第4题)
36-1=35(个)
35×6=210(米)
答:从第一棵到最后一棵的距离有210米。
探究点
2
不封闭路段两端都不植树的问题
问题:
1.
你都知道了什么?与例题1有什么不同?
2.
你认为一共要栽多少棵树?
例2:大象馆和猴山相距60
m。绿化队要在两馆间的小路两旁栽
树(两端不栽),相邻两棵树之间的距离是3
m。一共要栽
多少棵树?
自学提示:
1.请根据学习例题1的经验,先自主研究。
2.自主探索之后,先与同桌交流,然后在小组内交流。
3.将自己研究的成果,归纳总结出规律用式子去表示。
间隔数=总长÷间隔距离
棵数=间隔数-1
60÷3=20(个)
20-1=19(棵)
19×2
=38(棵)
1.为什么要用20减1呢?减的1你能说一说是在哪里吗?
2.为什么最后用19乘2?
问题:
1.
在两头都不种的情况下,棵数为什么会比间
隔数少1呢?
2.
少的“1”在哪呢,请你到图中指一指。
60米
棵数=间隔数-1
问题:
1.
比较两种情况,有什么相同?有什么不同?
2.
如果你忘记结论,可以怎样做呢?
棵数=间隔数+1
棵数=间隔数-1
100米
60米
两头种
两头不种
归纳总结:
在一条线段上植树(两端都不栽)的情况:
间隔数=总长÷间隔距离
棵数=间隔数-1
小试牛刀
1.
一条走廊长32
m,每隔4
m摆放一盆植物(两端不放)。
一共要放多少盆植物?
(选题源于教材P109第6题)
32÷4=8(个)
8-1=7(盆)
答:一共要放7盆植物。
5-1=4(次)
4×8=32(分钟)
答:锯完一共要花32分钟。
2.
一根木头长10m,要把它平均分成5段。每锯下一段需要
8分钟。锯完一共要花多少分钟?(选题源于教材P110第8题)
锯木头时,锯成n段,需要锯(n-1)次,锯每次的时间与次数相乘就是所需时间。
探究点
3
不封闭路段一端植树一端不植树的问题
例3:小明家门前有一条35
m的小路,绿化队要在路旁栽一
排树。每隔5
m栽一棵树(一端栽一端不栽)。一共
要栽多少棵?
该怎样列式计算呢?试一试吧!
35÷5=7(棵)
答:一共要栽7棵树。
为什么间隔数等于棵树?请用图示加以说明。
问题:1.
植树问题有哪几种情况?
每种情况中棵数与间隔数之间是什么关系?
2.
我们是通过什么方法得到这些结论的?
3.
如果你忘记或者混淆了这些情况,可以怎样做?
棵数=间隔数+1
100米
35米
两头种
60米
两头不种
棵数=间隔数-1
一头种
棵数=间隔数
间隔数=总长÷间隔距离
棵数=间隔数
归纳总结:
在一条线段上植树(一端栽,一端不栽)的情况:
42÷3=14(处)
答:全程一共有14处这样的服务点。
1.
马拉松比赛全程约42
km。平均每3
km设置一处饮水服务点
(起点不设,终点设),全程一共有多少处这样的服务点?
(选题源于教材P110第7题)
小试牛刀
两端都栽
棵数=间隔数+1
两端不栽
棵数=间隔数-1
一端栽一端不栽
棵树=间隔数
间隔数=总长÷间隔距离
植树问题基本解决思路:
1.要在学校门口一条长180
m的林荫路的一侧栽树,起点和终点都栽。如果每相邻两棵树之间的距离是3
m,需要多少棵树?
夯实基础
180÷3+1=61(棵)
答:需要61棵树。
2.在一条长40
m的小路两旁,每隔2
m栽一棵树(两端都栽),一共要栽多少棵树?
(40÷2+1)×2=42(棵)
答:一共要栽42棵树。
3.两根电线杆相距200
m,在两根电线杆之间每隔5
m栽一棵树(两端都不栽),一共可以栽多少棵树?
200÷5-1=39(棵)
答:一共要栽39棵树。
4.在绿化工程中,要在公园和动物园之间的马路两旁栽树(两端都不栽),每相邻两棵树之间相距4米,一共要栽多少棵树?
(400÷4-1)×2=198(棵)
答:一共要栽198棵树。
5.填一填。
学校有一条长为60
m的小道,计划在道路一旁栽树,每隔3
m栽一棵。
想:小道长( )m,每隔( )m栽一棵,有( )个间隔。
(1)如果两端都要栽树,那么一共要栽( )棵树。
(2)如果两端都不栽树,那么一共要栽( )棵树。
60
19
21
20
3
6.在150米长的直跑道的一旁每隔5米插一面彩旗(两端都要插),可以插多少面彩旗?
150÷5+1=31(面)
答:可以插31面彩旗。
7.某大桥的长为4500
m,在桥的两旁每隔45
m装一块广告牌(一端安装,一端不安装),这座大桥一共可以安装多少块广告牌?
4500÷45×2=200(块)
答:一共可以安装200块广告牌。
8.在一条长60米的村级小路两旁每隔5米栽一棵树苗,两端都栽,一共要准备多少棵树苗?
(60÷5+1)×2=26(棵)
答:一共要准备26棵树苗。
易错辨析
辨析:(60÷5+1)算出来的是一侧植树多少棵,在两侧植树时要乘以2。
