25.2用列举法求概率(第2课时) 课件(共25张PPT)+视频文件
文档属性
| 名称 | 25.2用列举法求概率(第2课时) 课件(共25张PPT)+视频文件 |  | |
| 格式 | ppt | ||
| 文件大小 | 35.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 14:51:30 | ||
图片预览






文档简介
(共27张PPT)
25.2
用列举法求概率
---第2课时
人教版
九年级上
教学目标
1.进一步理解等可能事件概率的意义.
2.学会运用树状图计算事件的概率.(重点)
3.会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.(难点)
情景导入
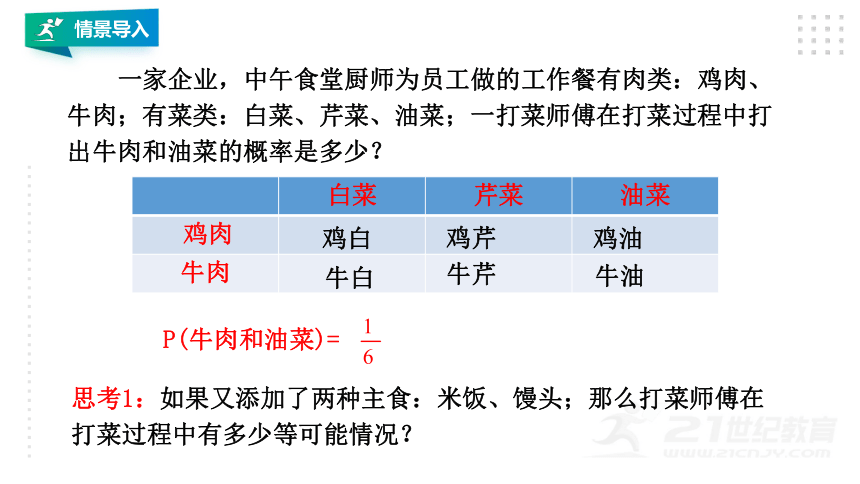
一家企业,中午食堂厨师为员工做的工作餐有肉类:鸡肉、牛肉;有菜类:白菜、芹菜、油菜;一打菜师傅在打菜过程中打出牛肉和油菜的概率是多少?
白菜
芹菜
油菜
鸡肉
牛肉
鸡白
鸡芹
鸡油
牛白
牛芹
牛油
P(牛肉和油菜)=
思考1:如果又添加了两种主食:米饭、馒头;那么打菜师傅在打菜过程中有多少等可能情况?
合作探究
合作探究
思考2:打菜师傅在打菜过程中打出鸡肉和米饭的概率是多少?
合作探究
画树状图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出试验的所有可能结果数n;
(4)数出随机事件A包含的结果数m,
(5)用概率公式进行计算.
典例精析
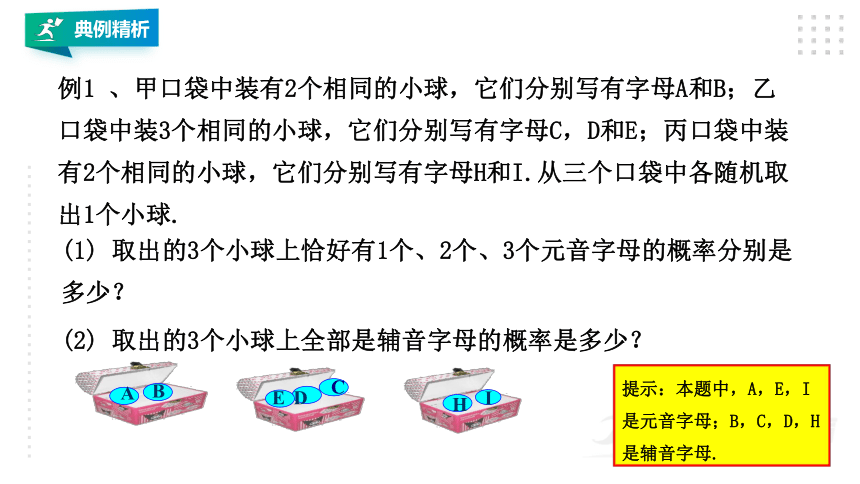
例1
、甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)
取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2)
取出的3个小球上全部是辅音字母的概率是多少?
提示:本题中,A,E,I是元音字母;B,C,D,H是辅音字母.
I
H
D
E
C
A
B
典例精析
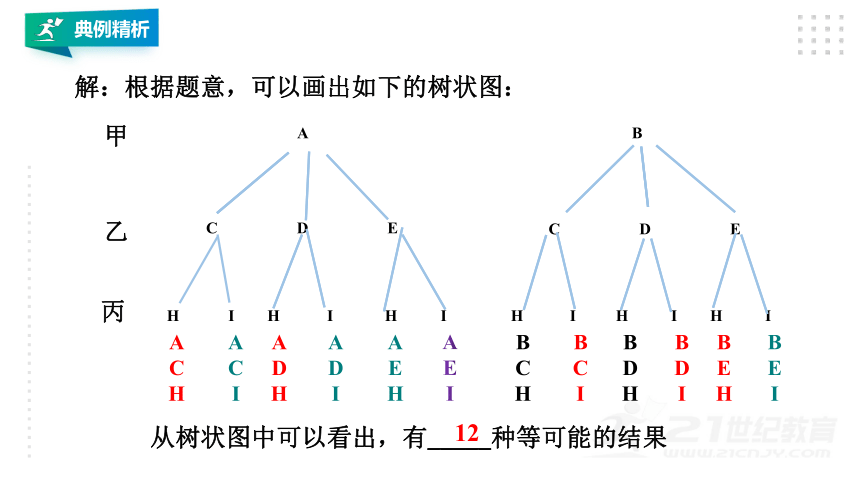
解:根据题意,可以画出如下的树状图:
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
ACH
AC
I
ADH
AD
I
AEH
BCH
BC
I
BDH
BD
I
BEH
BE
I
从树状图中可以看出,有_____种等可能的结果
12
典例精析
解:(1)取出的3个小球上恰好有1个元音字母的结果有5种,即
ACH、ADH、BCI、BDI、BEH,所以:
P(1个元音)=
恰好有2个元音字母的结果有4种,即ACI、ADI、AEH、BEI,所以:
P(2个元音)=
全部为元音字母的结果有1种,即AEI,所以:
P(3个元音)=
(2)取出的3个小球上全部是辅音字母的结果有2种,即BCH、
BDH,所以:
P(3个辅音)=
趁热打铁
1.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)
三辆车全部继续直行;
(2)
两车向右,一车向左;
(3)
至少两车向左.
趁热打铁
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种等可能
行驶结果
(2)
P(两车向右,一车向左)=
;
(1)
P(全部继续直行)=
;
(3)
P(至少两车向左)=
开始
趁热打铁
2、某班有1名男生、2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选一人去领奖,求两人都是女生的概率.
解:设两名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.
趁热打铁
开始
获演唱奖的
获演奏奖的
男
女''
女'
女1
男2
男1
女2
女1
男2
男1
女1
男2
男1
女2
女2
共有12种结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)=
合作探究
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
方法归纳:
综合演练
2.
a、b、c、d
四本不同的书放入一个书包,至少放一本,最多放两本,共有
种不同的放法.
1.九(2)班第5学习小组共有2位女生和3位男生.一次数学课上,老师随机让该学习小组的2位同学上台演示解题过程(每个同学上台演示的可能性相同),则上台演示解题过程的2位同学都是女生的概率等于( )
10
C
A.
B.
C.
D.
综合演练
3.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包、一个糖包和一个韭菜包,C盘中有一个酸菜包、一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
综合演练
解:根据题意,画出树状图如下
由树状图得,所有可能出现的结果有18种,它们出现的可能性相等.选的包子全部是酸菜包有2种,所以选的包子全部是酸菜包的概率是:P(全是酸菜包)
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
综合演练
4、甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,
写出A发生的所有可能结果;
(3)求P(A).
综合演练
解:(1)
第二次
第三次
结果
开始:甲
共有八种可能的结果,每种结果出现的可能性相同;
(2)
传球三次后,球又回到甲手中,事件A发生有两种可能
出现结果(乙,丙,甲)(丙,乙,甲);
乙
丙
第一次
甲
甲
丙
乙
甲
甲
丙
丙
乙
乙
乙
丙
(丙,乙,丙)
(乙,甲,丙)
(乙,丙,甲)
(乙,丙,乙)
(丙,甲,乙)
(丙,甲,丙)
(丙,乙,甲)
(乙,甲,乙)
(3)
P(A)=
提能训练
1.为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
提能训练
(1)m=______%,这次共抽取了______名学生进行调查;并补全条形图;
(2)请你估计该校约有______名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用画树状图的方法,求抽到一男一女学生的概率是多少?
提能训练
解:(1)m=100%-14%-8%-24%-34%=20%;
∵跳绳的人数有4人,占的百分比为8%,
∴4÷8%=50;
故答案为:20,50;
如图所示;50×20%=10(人).
提能训练
(2)1500×24%=360;
故答案为:360;
(3)画树状图如下:
男1
男2
男3
女
男2
男3
女
男1
男3
女
男1
男2
女
男1
男2
男3
所有可能出现的结果共有12种,并且每种情况出现的可能性相等,其中一男一女的情况有6种,所以P(抽到一男一女)=
课堂总结
说一说
1、什么情况用列表法简单适用?什么时候用树状图适用?
2、用树状图求概率的步骤是什么?
3、用树状图求概率需注意什么?
本节课你有哪些收获?
作业布置
习题25.2
P140页:4、5、6
https://www.21cnjy.com/help/help_extract.php
25.2
用列举法求概率
---第2课时
人教版
九年级上
教学目标
1.进一步理解等可能事件概率的意义.
2.学会运用树状图计算事件的概率.(重点)
3.会正确用画树状图法求出所有可能出现的结果,并计算事件的概率.(难点)
情景导入
一家企业,中午食堂厨师为员工做的工作餐有肉类:鸡肉、牛肉;有菜类:白菜、芹菜、油菜;一打菜师傅在打菜过程中打出牛肉和油菜的概率是多少?
白菜
芹菜
油菜
鸡肉
牛肉
鸡白
鸡芹
鸡油
牛白
牛芹
牛油
P(牛肉和油菜)=
思考1:如果又添加了两种主食:米饭、馒头;那么打菜师傅在打菜过程中有多少等可能情况?
合作探究
合作探究
思考2:打菜师傅在打菜过程中打出鸡肉和米饭的概率是多少?
合作探究
画树状图求概率的基本步骤:
(1)明确一次试验的几个步骤及顺序;
(2)画树状图列举一次试验的所有可能结果;
(3)数出试验的所有可能结果数n;
(4)数出随机事件A包含的结果数m,
(5)用概率公式进行计算.
典例精析
例1
、甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装3个相同的小球,它们分别写有字母C,D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I.从三个口袋中各随机取出1个小球.
(1)
取出的3个小球上恰好有1个、2个、3个元音字母的概率分别是多少?
(2)
取出的3个小球上全部是辅音字母的概率是多少?
提示:本题中,A,E,I是元音字母;B,C,D,H是辅音字母.
I
H
D
E
C
A
B
典例精析
解:根据题意,可以画出如下的树状图:
丙
甲
乙
B
A
E
C
D
E
C
D
I
H
I
H
I
H
I
H
I
H
I
H
ACH
AC
I
ADH
AD
I
AEH
BCH
BC
I
BDH
BD
I
BEH
BE
I
从树状图中可以看出,有_____种等可能的结果
12
典例精析
解:(1)取出的3个小球上恰好有1个元音字母的结果有5种,即
ACH、ADH、BCI、BDI、BEH,所以:
P(1个元音)=
恰好有2个元音字母的结果有4种,即ACI、ADI、AEH、BEI,所以:
P(2个元音)=
全部为元音字母的结果有1种,即AEI,所以:
P(3个元音)=
(2)取出的3个小球上全部是辅音字母的结果有2种,即BCH、
BDH,所以:
P(3个辅音)=
趁热打铁
1.经过某十字路口的汽车,可能直行,也可能向左转或向右转.如果这三种可能性大小相同,求三辆汽车经过这个十字路口时,下列事件的概率:
(1)
三辆车全部继续直行;
(2)
两车向右,一车向左;
(3)
至少两车向左.
趁热打铁
第一辆
左
右
左
右
左直右
第二辆
第三辆
直
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种等可能
行驶结果
(2)
P(两车向右,一车向左)=
;
(1)
P(全部继续直行)=
;
(3)
P(至少两车向左)=
开始
趁热打铁
2、某班有1名男生、2名女生在校文艺演出中获演唱奖,另有2名男生、2名女生获演奏奖.从获演唱奖和演奏奖的学生中各任选一人去领奖,求两人都是女生的概率.
解:设两名领奖学生都是女生的事件为A,两种奖项各任选1人的结果用“树状图”来表示.
趁热打铁
开始
获演唱奖的
获演奏奖的
男
女''
女'
女1
男2
男1
女2
女1
男2
男1
女1
男2
男1
女2
女2
共有12种结果,且每种结果出现的可能性相等,其中2名都是女生的结果有4种,所以事件A发生的概率为P(A)=
合作探究
当试验包含两步时,列表法比较方便;当然,此时也可以用树形图法;
当事件要经过多个(三个或三个以上)步骤完成时,应选用树状图法求事件的概率.
方法归纳:
综合演练
2.
a、b、c、d
四本不同的书放入一个书包,至少放一本,最多放两本,共有
种不同的放法.
1.九(2)班第5学习小组共有2位女生和3位男生.一次数学课上,老师随机让该学习小组的2位同学上台演示解题过程(每个同学上台演示的可能性相同),则上台演示解题过程的2位同学都是女生的概率等于( )
10
C
A.
B.
C.
D.
综合演练
3.现有A、B、C三盘包子,已知A盘中有两个酸菜包和一个糖包,B盘中有一个酸菜包、一个糖包和一个韭菜包,C盘中有一个酸菜包、一个糖包以及一个馒头.老师就爱吃酸菜包,如果老师从每个盘中各选一个包子(馒头除外),那请你帮老师算算选的包子全部是酸菜包的概率是多少?
A
B
C
综合演练
解:根据题意,画出树状图如下
由树状图得,所有可能出现的结果有18种,它们出现的可能性相等.选的包子全部是酸菜包有2种,所以选的包子全部是酸菜包的概率是:P(全是酸菜包)
A盘
B盘
C盘
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
酸
酸
糖
韭
酸
糖
酸
糖
酸
糖
糖
酸
糖
韭
酸
糖
酸
糖
酸
糖
综合演练
4、甲、乙、丙三人做传球的游戏,开始时,球在甲手中,每次传球,持球的人将球任意传给其余两人中的一人,如此传球三次.
(1)写出三次传球的所有可能结果(即传球的方式);
(2)指定事件A:“传球三次后,球又回到甲的手中”,
写出A发生的所有可能结果;
(3)求P(A).
综合演练
解:(1)
第二次
第三次
结果
开始:甲
共有八种可能的结果,每种结果出现的可能性相同;
(2)
传球三次后,球又回到甲手中,事件A发生有两种可能
出现结果(乙,丙,甲)(丙,乙,甲);
乙
丙
第一次
甲
甲
丙
乙
甲
甲
丙
丙
乙
乙
乙
丙
(丙,乙,丙)
(乙,甲,丙)
(乙,丙,甲)
(乙,丙,乙)
(丙,甲,乙)
(丙,甲,丙)
(丙,乙,甲)
(乙,甲,乙)
(3)
P(A)=
提能训练
1.为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况,在全校范围内随机抽查部分学生,对他们喜爱的体育项目(每人只选一项)进行了问卷调查,将统计数据绘制成如图两幅不完整统计图,请根据图中提供的信息解答下列各题.
提能训练
(1)m=______%,这次共抽取了______名学生进行调查;并补全条形图;
(2)请你估计该校约有______名学生喜爱打篮球;
(3)现学校准备从喜欢跳绳活动的4人(三男一女)中随机选取2人进行体能测试,请利用画树状图的方法,求抽到一男一女学生的概率是多少?
提能训练
解:(1)m=100%-14%-8%-24%-34%=20%;
∵跳绳的人数有4人,占的百分比为8%,
∴4÷8%=50;
故答案为:20,50;
如图所示;50×20%=10(人).
提能训练
(2)1500×24%=360;
故答案为:360;
(3)画树状图如下:
男1
男2
男3
女
男2
男3
女
男1
男3
女
男1
男2
女
男1
男2
男3
所有可能出现的结果共有12种,并且每种情况出现的可能性相等,其中一男一女的情况有6种,所以P(抽到一男一女)=
课堂总结
说一说
1、什么情况用列表法简单适用?什么时候用树状图适用?
2、用树状图求概率的步骤是什么?
3、用树状图求概率需注意什么?
本节课你有哪些收获?
作业布置
习题25.2
P140页:4、5、6
https://www.21cnjy.com/help/help_extract.php
同课章节目录
