23.5位似图形 课件(20张PPT)
文档属性
| 名称 | 23.5位似图形 课件(20张PPT) | 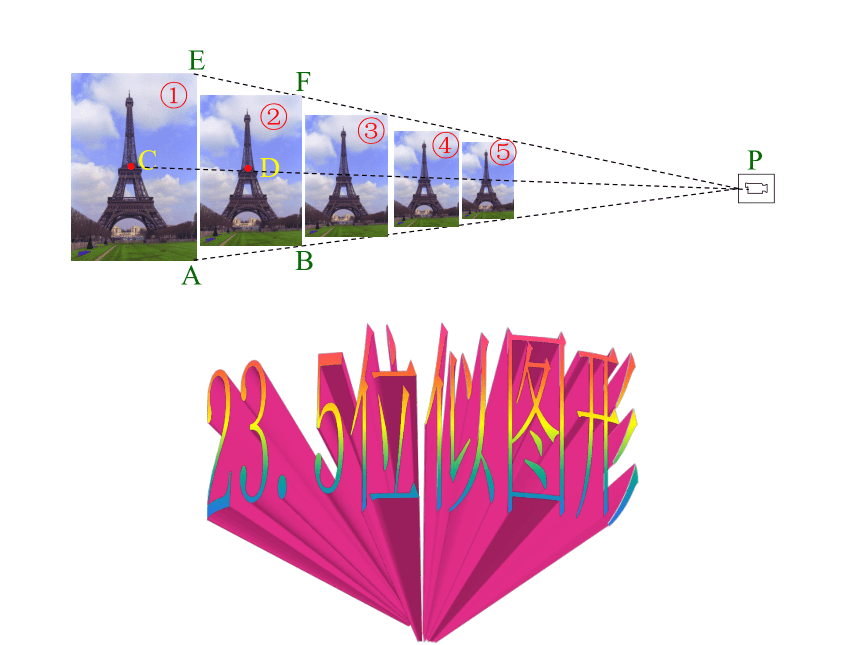 | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 15:27:10 | ||
图片预览





文档简介
(共20张PPT)
①
P
A
②
③
④
⑤
B
C
D
E
F
.
.
1.
前面我们已经学习了图形的哪些变换?
相似:相似比.
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
轴对称:对称轴,
观察与思考
?
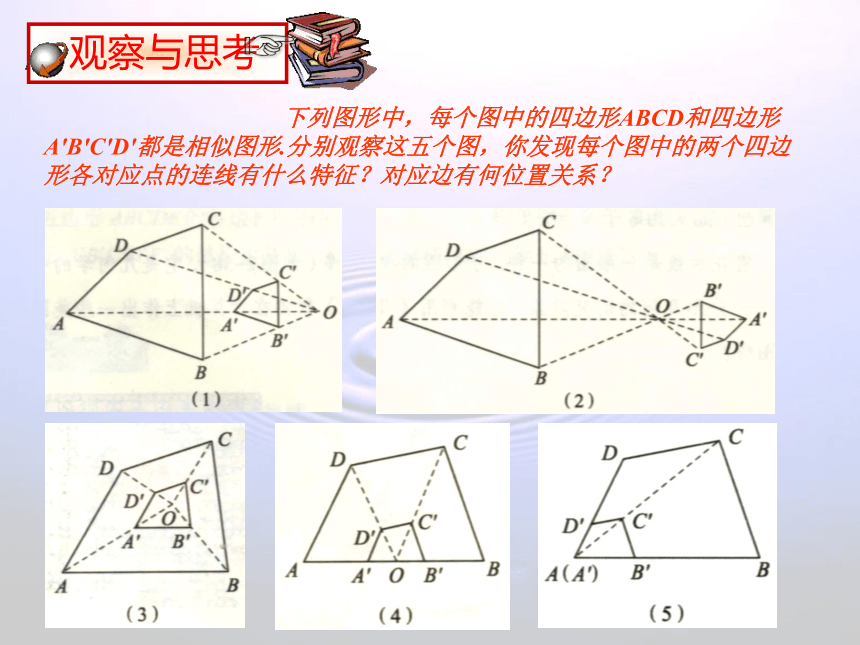
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?对应边有何位置关系?
概念与性质
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时两个相似图形的相似比又叫做它们的位似比.
相似
对应点的连线相交一点
对应边平行
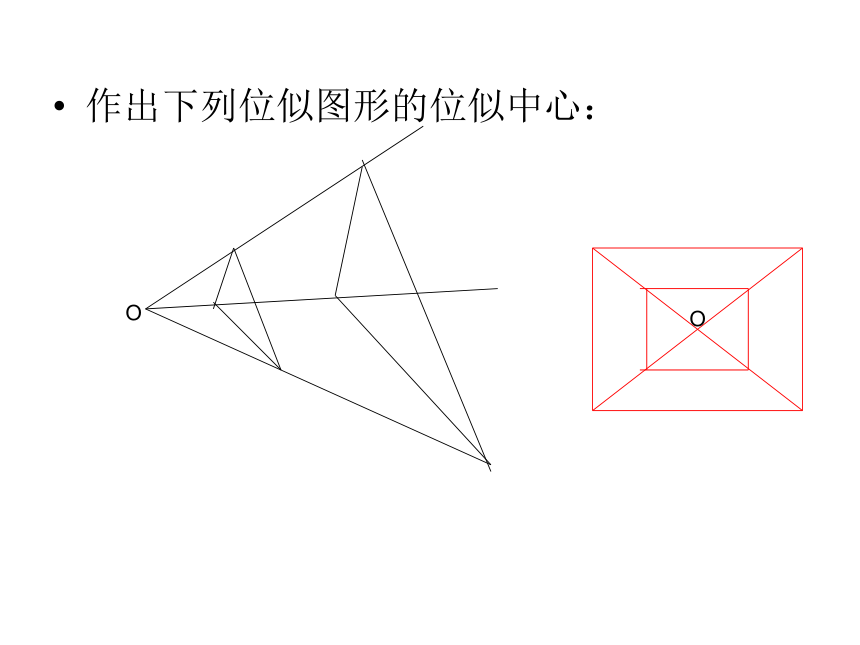
作出下列位似图形的位似中心:
O
O
判断下面的正方形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
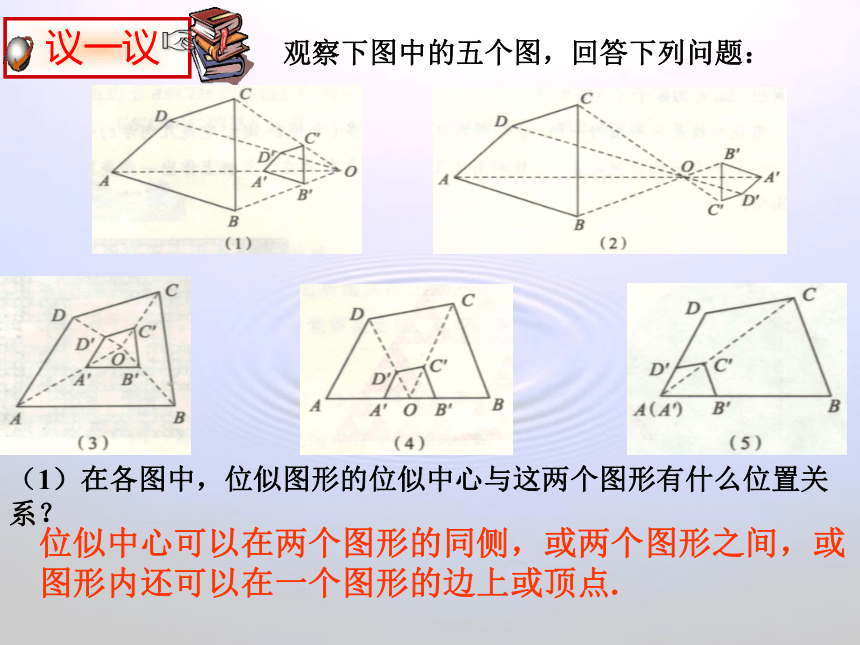
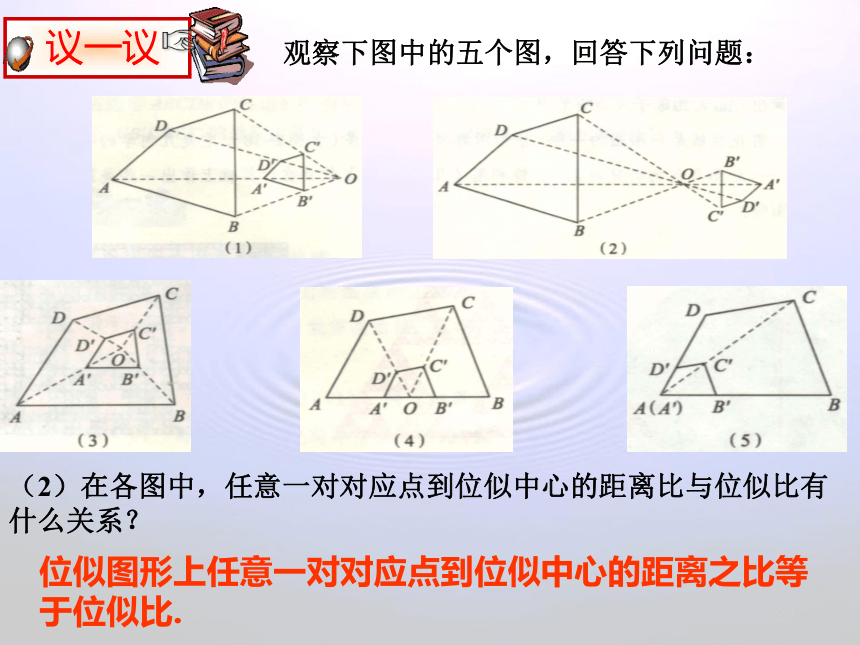
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有什么位置关系?
位似中心可以在两个图形的同侧,或两个图形之间,或图形内还可以在一个图形的边上或顶点.
议一议
?
观察下图中的五个图,回答下列问题:
(2)在各图中,任意一对对应点到位似中心的距离比与位似比有什么关系?
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
议一议
?
2.
位似图形的性质
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.
概念与性质
(3)位似图形中的对应线段平行(或在一条直线上).
(1)位似图形是相似图形,具备相似图形的所有性质
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=(
)。
O
A
A’
B
C
B’
C’
1:2
D
E
F
A
O
B
C
D
E
F
O
A
B
C
利用位似可以把一个图形放大或缩小
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
图形与画法
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
画位似图形的
步骤有哪些?
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),
B′(2,0)
观察对应点之间的坐标的变化,你有什么发现?
位似变换与坐标
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,
如果位似变换是以原点为位似中心,
相似比为k,
那么位似图形对应点的坐标的比等于k或-k
例如:点A(x,y)的对应点为A’,则A’点的坐标可以这样确定
归纳:
xA’=xA×k
,
yA'=yA×k
xA’=xA×(-k)
,yA'=yA×(-k)
或
即A’(kx,ky)
即A’(-kx,-ky)
△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,点A的对应点A′的坐标为____________
A′(
4,6
)或(-4,-6)
x
y
o
例题.在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
x
y
o
B
如图表示△AOB和把它缩小后得到的△COD,写出它们的相似比
A
C
D
练一练:
1.画出基本图形
2.选取位似中心
3.根据条件确定对应点,并描出对应点
4.顺次连结各对应点,所成的图形就是
所求的图形
一、定义及性质:
在平面直角坐标系中,如果位似变换
是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k
二、位似图形的画法:
三、位似变换与坐标的关系:
课堂小结
回味无穷
位似图形的概念:
如果两个图形不仅形状相同,而且所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形是相似图形,具备相似图形的所有性质
2.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
3.位似图形中的对应线段平行(或在一条直线上).
课堂小结
我们学过的图形变换有:
平移,轴对称,旋转,位似。
(1)平移:
上下移:横坐标不变,纵坐标随之平移
左右移:纵坐标不变,横坐标随之平移
(2)轴对称
关于x轴对称:横坐标不变,纵坐标互为相反数
关于y轴对称:纵坐标不变,横坐标互为相反数
(3)旋转
绕原点旋转180度(中心对称):横坐标、纵坐标都互为相反数
(4)位似
以原点为位似中心,相似比为k:位似图形对应点的坐标的比等于k或-k
①
P
A
②
③
④
⑤
B
C
D
E
F
.
.
1.
前面我们已经学习了图形的哪些变换?
相似:相似比.
平移:平移的方向,平移的距离.
注:图形这些不同的变换是我们学习几何必不可少的重要工具,它不但装点了我们的生活,而且是学习后续知识的基础.
回顾与反思
下面请欣赏如下图形的变换
旋转:(中心对称)旋转中心,旋转方向,旋转角度.
轴对称:对称轴,
观察与思考
?
下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?对应边有何位置关系?
概念与性质
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时两个相似图形的相似比又叫做它们的位似比.
相似
对应点的连线相交一点
对应边平行
作出下列位似图形的位似中心:
O
O
判断下面的正方形是不是位似图形?
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
观察下图中的五个图,回答下列问题:
(1)在各图中,位似图形的位似中心与这两个图形有什么位置关系?
位似中心可以在两个图形的同侧,或两个图形之间,或图形内还可以在一个图形的边上或顶点.
议一议
?
观察下图中的五个图,回答下列问题:
(2)在各图中,任意一对对应点到位似中心的距离比与位似比有什么关系?
位似图形上任意一对对应点到位似中心的距离之比等于位似比.
议一议
?
2.
位似图形的性质
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.
概念与性质
(3)位似图形中的对应线段平行(或在一条直线上).
(1)位似图形是相似图形,具备相似图形的所有性质
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=(
)。
O
A
A’
B
C
B’
C’
1:2
D
E
F
A
O
B
C
D
E
F
O
A
B
C
利用位似可以把一个图形放大或缩小
1.如图,已知△ABC和点O.以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
图形与画法
如果把位似图形放到直角体系中,又如何去探究位似变换与坐标之间的关系呢?
画位似图形的
步骤有哪些?
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),
B′(2,0)
观察对应点之间的坐标的变化,你有什么发现?
位似变换与坐标
B'
A'
x
y
B
A
o
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:3,把线段AB缩小.
A′(2,1),B′(2,0)
A〞
B〞
A〞(-2,-1),B(-2,0)
在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.
观察对应点之间的坐标的变化,你有什么发现?
在平面直角坐标系中,
如果位似变换是以原点为位似中心,
相似比为k,
那么位似图形对应点的坐标的比等于k或-k
例如:点A(x,y)的对应点为A’,则A’点的坐标可以这样确定
归纳:
xA’=xA×k
,
yA'=yA×k
xA’=xA×(-k)
,yA'=yA×(-k)
或
即A’(kx,ky)
即A’(-kx,-ky)
△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,点A的对应点A′的坐标为____________
A′(
4,6
)或(-4,-6)
x
y
o
例题.在平面直角坐标系中,
四边形ABCD的四个顶点的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2的位似图形.
A′(
-3,3
),
B′(
-4,1
),
C′(
-2,0
),
D′(
-1,2
)
B
A
C
D
A′
B′
C′
D′
你还有其他办法吗?试试看.
x
y
o
B
如图表示△AOB和把它缩小后得到的△COD,写出它们的相似比
A
C
D
练一练:
1.画出基本图形
2.选取位似中心
3.根据条件确定对应点,并描出对应点
4.顺次连结各对应点,所成的图形就是
所求的图形
一、定义及性质:
在平面直角坐标系中,如果位似变换
是以原点为位似中心,相似比为k,
那么位似图形对应点的坐标的比等于k或-k
二、位似图形的画法:
三、位似变换与坐标的关系:
课堂小结
回味无穷
位似图形的概念:
如果两个图形不仅形状相同,而且所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
位似图形的性质:
1.位似图形是相似图形,具备相似图形的所有性质
2.位似图形上的任意一对对应点到位似中心的距离之比等于位似比
3.位似图形中的对应线段平行(或在一条直线上).
课堂小结
我们学过的图形变换有:
平移,轴对称,旋转,位似。
(1)平移:
上下移:横坐标不变,纵坐标随之平移
左右移:纵坐标不变,横坐标随之平移
(2)轴对称
关于x轴对称:横坐标不变,纵坐标互为相反数
关于y轴对称:纵坐标不变,横坐标互为相反数
(3)旋转
绕原点旋转180度(中心对称):横坐标、纵坐标都互为相反数
(4)位似
以原点为位似中心,相似比为k:位似图形对应点的坐标的比等于k或-k
