23.5位似图形 课件(21张PPT)
文档属性
| 名称 | 23.5位似图形 课件(21张PPT) | 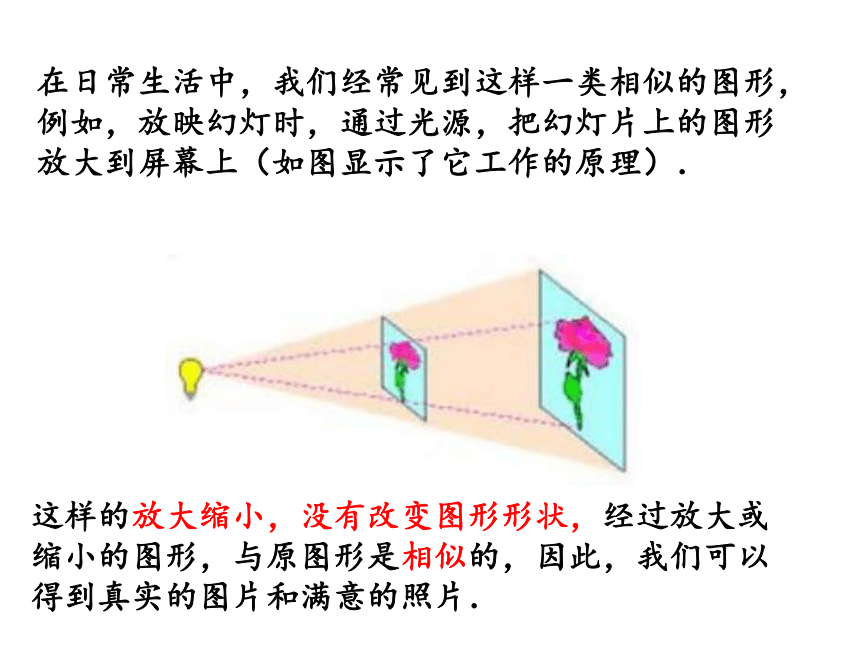 | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-15 15:28:22 | ||
图片预览








文档简介
(共21张PPT)
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷的画出一个图形的相似图形呢?
23.5位似图形
探究一:怎样将一个图形放大或缩小,
如图,任意五边形ABCDE,你能将它放大到原来的2倍吗?
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使
OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=2
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
则五边形A’B’C’D’E’就是所求作的五边形.
A
B
C
E
D
O
A’
B’
C’
D’
E’
思考:
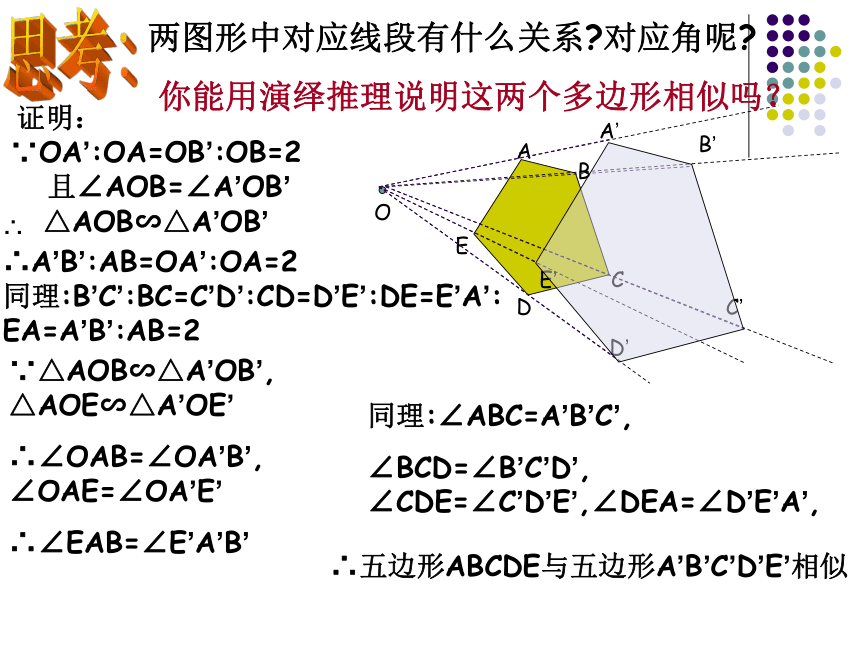
两图形中对应线段有什么关系?对应角呢?
你能用演绎推理说明这两个多边形相似吗?
同理:∠ABC=A’B’C’,
∠BCD=∠B’C’D’,
∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴
证明:
∵OA’:OA=OB’:OB=2
且∠AOB=∠A’OB’
△AOB∽△A’OB’
∴A’B’:AB=OA’:OA=2
同理:B’C’:BC=C’D’:CD=D’E’:DE=E’A’:
EA=A’B’:AB=2
∵△AOB∽△A’OB’,
△AOE∽△A’OE’
∴∠OAB=∠OA’B’,
∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
∴五边形ABCDE与五边形A’B’C’D’E’相似
2.
分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得
3.
顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
把四边形ABCD缩小到原来的,
1.
在四边形外任选一点O(如图),
四边形A’B’C’D’即为所求
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A‘
,B’
、C‘
、D’
,
使得
呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
探究
A’B’C’D’即为所求
画图一般步骤:
1.确定位似中心
2.分别连接位似中心和能代表原图形的关键点
3.根据相似比,找出所做位似图形的对应点
4.顺次连接上述各点得到放大或缩小的图形
利用刚才的办法把一个图形放大或缩小.那么这种相似有什么特征?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点
O
O
O
探究二:位似的概念与特征
这个点叫做位似中心
1、位似图形的概念:如果两个图形不仅相似,而且对应顶点的连线相交于一点,
那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比。
相似
对应顶点的连线相交一点
对应边互相平行
(或在同一直线上)
明确
利用位似,可以将一个图形放大或缩小.
观察下图中的五个图,回答下列问题:
在各图中,位似图形的位似中心与这两个图形有什么位置关系?
位似中心可以在两个图形的同侧,或两个图形之间,或图形内还可以在一个图形的边上或顶点.
2、位似中心与原图的位置关系:
3、判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?
是
是
不一定
4、判断下面的正方形是不是位似图形?
想一想
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
5、位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.
练习解析
如果?OAB和
?OCD是位似图形,那么AB∥CD吗?为什么?
解:AB∥CD.理由是:
?OAB和
?OCD是位似图形,
?OAB∽?OCD
∠OAB=∠C
AB∥CD.
A
B
C
D
O
注意:对应边OB与OD在同一直线
上.
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=(
)。
O
A
A’
B
C
B’
C’
1:2
6、作出下列位似图形的位似中心:
位似中心的作法
O
点O即为所求
位似图形的概念:
如果两个图形不仅形状相似,而且每组对应顶点所在的直线都经过同一个点,
那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
课堂小结
位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
至此,我们己经学习了四种变换;平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
再见
这样的放大缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和满意的照片.
在日常生活中,我们经常见到这样一类相似的图形,例如,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上(如图显示了它工作的原理).
相似与轴对称,平移,旋转一样,也是图形之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷的画出一个图形的相似图形呢?
23.5位似图形
探究一:怎样将一个图形放大或缩小,
如图,任意五边形ABCDE,你能将它放大到原来的2倍吗?
A
B
C
E
D
1.任取一点O
O
2.以O为端点,作射线OA,OB,OC,OD,OE
3.分别在射线OA,OB,OC,OD,OE上,取点A’,B’,C’,D’,E’,使
OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=2
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’
E
则五边形A’B’C’D’E’就是所求作的五边形.
A
B
C
E
D
O
A’
B’
C’
D’
E’
思考:
两图形中对应线段有什么关系?对应角呢?
你能用演绎推理说明这两个多边形相似吗?
同理:∠ABC=A’B’C’,
∠BCD=∠B’C’D’,
∠CDE=∠C’D’E’,∠DEA=∠D’E’A’,
∴
证明:
∵OA’:OA=OB’:OB=2
且∠AOB=∠A’OB’
△AOB∽△A’OB’
∴A’B’:AB=OA’:OA=2
同理:B’C’:BC=C’D’:CD=D’E’:DE=E’A’:
EA=A’B’:AB=2
∵△AOB∽△A’OB’,
△AOE∽△A’OE’
∴∠OAB=∠OA’B’,
∠OAE=∠OA’E’
∴∠EAB=∠E’A’B’
∴五边形ABCDE与五边形A’B’C’D’E’相似
2.
分别在线段OA、OB、OC、OD上取点A'、B'、C'、D',使得
3.
顺次连接点A'、B'、C'、D',所得四边形A'B'C'D'就是所要求的图形.
O
D
A
B
C
A'
B'
C'
D'
把四边形ABCD缩小到原来的,
1.
在四边形外任选一点O(如图),
四边形A’B’C’D’即为所求
对于上面的问题,还有其他方法吗?如果在四边形外任选一个点O,分别在OA、OB、OC、OD的反向延长线上取A‘
,B’
、C‘
、D’
,
使得
呢?如果点O取在四边形ABCD内部呢?分别画出这时得到的图形.
O
D
A
B
C
A'
B'
C'
D'
O
D
A
B
C
探究
A’B’C’D’即为所求
画图一般步骤:
1.确定位似中心
2.分别连接位似中心和能代表原图形的关键点
3.根据相似比,找出所做位似图形的对应点
4.顺次连接上述各点得到放大或缩小的图形
利用刚才的办法把一个图形放大或缩小.那么这种相似有什么特征?
图中每幅图中的两个多边形不仅相似,而且对应顶点的连线相交于一点
O
O
O
探究二:位似的概念与特征
这个点叫做位似中心
1、位似图形的概念:如果两个图形不仅相似,而且对应顶点的连线相交于一点,
那么这样的两个图形叫做位似图形,这个点叫做位似中心.这时的相似比又叫位似比。
相似
对应顶点的连线相交一点
对应边互相平行
(或在同一直线上)
明确
利用位似,可以将一个图形放大或缩小.
观察下图中的五个图,回答下列问题:
在各图中,位似图形的位似中心与这两个图形有什么位置关系?
位似中心可以在两个图形的同侧,或两个图形之间,或图形内还可以在一个图形的边上或顶点.
2、位似中心与原图的位置关系:
3、判断下列各对图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′;
(2)等边三角形ABC与等边三角形A′B′C′.
思考:是否相似图形都是位似图形?
是
是
不一定
4、判断下面的正方形是不是位似图形?
想一想
(1)
不是
A
C
D
B
F
E
G
显然,位似图形是相似图形的特殊情形.相似图形不一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
5、位似图形的性质
性质:位似图形上任意一对对应点到位似中心的距离之比等于位似比.
练习解析
如果?OAB和
?OCD是位似图形,那么AB∥CD吗?为什么?
解:AB∥CD.理由是:
?OAB和
?OCD是位似图形,
?OAB∽?OCD
∠OAB=∠C
AB∥CD.
A
B
C
D
O
注意:对应边OB与OD在同一直线
上.
若△ABC与△A’B’C’的相似比为:1:2,则OA:OA’=(
)。
O
A
A’
B
C
B’
C’
1:2
6、作出下列位似图形的位似中心:
位似中心的作法
O
点O即为所求
位似图形的概念:
如果两个图形不仅形状相似,而且每组对应顶点所在的直线都经过同一个点,
那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.
课堂小结
位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比
至此,我们己经学习了四种变换;平移、轴对称、旋转和位似,你能说出它们之间的异同吗?在图所示的图案中,你能找到这些变换吗?
再见
