华东师大版七上数学 3.2代数式的值 课件(共17张PPT)
文档属性
| 名称 | 华东师大版七上数学 3.2代数式的值 课件(共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 241.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 13:16:16 | ||
图片预览






文档简介
(共17张PPT)
§3.2
代数式的值
问题情境、学生活动
一、传数游戏
规则:班级同学按4个同学一组进行分组,做一
个传数游戏。
第一个同学任意报一个数给第二个同学,
第二个同学把这个数加1传给第三个同学,
第三个同学再把听到的数平方后传给第四个同学
第四个同学把听到的数减去1报出答案.
概括
问题情境、学生活动
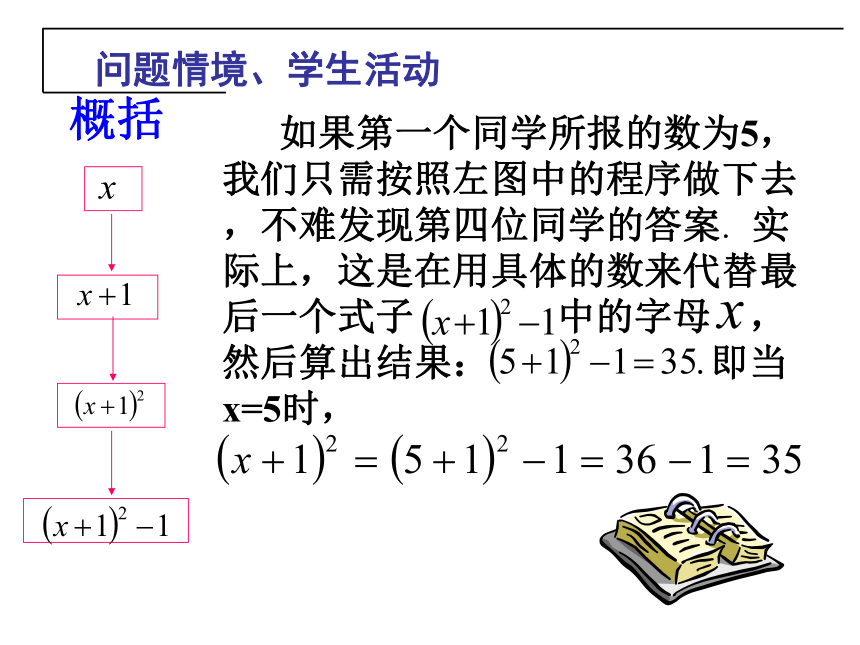
如果第一个同学所报的数为5,我们只需按照左图中的程序做下去,不难发现第四位同学的答案.
实际上,这是在用具体的数来代替最后一个式子
中的字母
,然后算出结果:
即当x=5时,
探索新知
概念
一般地,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值.
数学应用
例1:当a=2,b=-1,c=-3时,求下列各代数式的值.
⑴b2-4ac;
⑵a2+b2+c2+2ab+2bc+2ac;
⑶(a+b+c)2.
⑴解:当a=2,b=-1,c=-3时
b2-4ac=
(-1)2-4×2×(-3)
=1+24
=25
⑵解:当a=2,b=-1,c=-3时
a2+b2+c2+2ab+2bc+2ac
=22+(-1)2+(-3)2+2×2×(-1)+2×(-1)
×
(-3)+2×2×(-3)
=4+1+9-4+6+12
=4
⑶解:当a=2,b=-1,c=-3时
(a+b+c)2=(2-1-3)2
=4
观察⑵
⑶
两题的结果,你有什么想法?
尝试体验
1.当a=3时,5a=_____;
2.当s=-2时,
2s=_____;
3.当x=
时,
=__;
4.当b=-3时,
=___;
5.当a=2,b=-1时,a-b=__.
15
-4
8
3
1
概念小结
1、求代数式的值的具体步骤,注意点是什么?
①求代数式的值的步骤:
(1)代入,将字母所取的值代入代数式中;
(2)计算,按照代数式指明的运算进行,计算出结果.
②注意的几个问题:
(1)由于代数式的值是由代数式中的字母所取的值确定的,所以代入数值前应先指明字母的取值,把“当……时”写出来;
(2)如果字母的值是负数、分数,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号.
2、口诀:挖去字母变成数,
数字符号全保留,分数负数添括号,运算关系总不变,准确计算不马虎.
数学运用
例2.某企业去年的年产值为a亿元,今年比去年增长了10%。如果明年还能按这个速度增长,请你预测一下,该企业明年的年产值能达到多少亿元?如果去年的年产值是2亿元,那么预计明年的年产值是多少亿元?
解:由题意可得,今年的年产值为
亿元
(1+10%)a
于是明年的年产值为
a(1+10%)(1+10%)=1.21a
若去年的年产值为2亿元,则明年的年产值为
1.21a=1.21×2=2.42(亿元).
答:该企业明年的年产值将能达到1.21a亿元。由去年的年产值是2亿元,可以预测明年的年产值是2.42亿元.
1.按右边图示的程序计算,若开始输入的n值为2,则最后输出的结果是
.
231
输入n
计算
的值
>200
输出结果
yes
no
巩固提升
(逆用乘法分配律)
数学应用
例3:若x+2y2+5的值为7,求代数式3x+6y2+4的值.
解:∵
x+2y2+5=7
∴x+2y2=2
∴
3x+6y2+4
=3(x+2y2)
+4
=3×2+4
=10
1、根据下列各组x、y
的值,分别求出代数式x2
+2xy+y2
与
x2
-2xy+y2
的值:(1)x=2,y=3;(2)x=-2,y=-4.
解:
(1)当x=2,y=3时,
x2
+2xy+y2=22+2×2×3+32
=4+12+9=25
x2
-2xy+y2=22-2×2×3+32
=4-12+9
=1
数学应用
练一练
(2)当x=-2,y=-4时,
x2
+2xy+y2=(-2)2+2×(-2)
×
(-4)
+(-4)2
=4+16+16
=36
x2
-2xy+y2=(-2)2-2×(-2)
×
(-4)
+(-4)2
=4-16+16
=4
数学应用
回顾反思(小结)
1、求代数式的值的步骤:
2、求代数式的值的注意事项:
(1)代入数值前应先指明字母的取值,把“当……时”写出来;
(2)如果字母的值是负数、分数,并且要计算它的乘方,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号;
3、相同的代数式可以看作一个字母——整体代换;
4、代数式的值的广泛应用:计算机编程(包括用
Excel处理数据等)、经济、生活等方面的应用.
(1)代入,(2)计算;
现有两个代数式:3x+1…(1)
…(2)如果随意给出一个正整数,记为x,那么利用这个正整数,我们都可以根据代数式(1)或(2)求出一个对应值.
我们约定一个规则:若正整数x为奇数,我们就根据(1)式求对应值;若正整数x为偶数,我们就根据
(2)式求对应值.例如根据这种规则,若取正整数x为18(偶数),则由(2)式求得对应值为9;而正整数9(奇数),由(1)式求得对应值为28;同样,正整数28(偶数)对应14…我们感兴趣的是,从某一个正整数出发,不断地这样对应下去,会是一个什么样的结果呢?也许这是一个非常吸引人的数学游戏.
思考:有趣的“3x+1”问题
下面我们以正数18为例,不断地做下去,如下图所示,最后竟出现了一个循环:4,2,1,4,2,1,…….
9
18
28
14
7
22
11
20
40
13
26
52
17
34
10
5
16
8
4
2
1
再取一个奇数试试看。比如取x为21,如下图所示,结果是一样的——仍是一个同样的循环.
16
8
4
2
1
21
32
64
§3.2
代数式的值
问题情境、学生活动
一、传数游戏
规则:班级同学按4个同学一组进行分组,做一
个传数游戏。
第一个同学任意报一个数给第二个同学,
第二个同学把这个数加1传给第三个同学,
第三个同学再把听到的数平方后传给第四个同学
第四个同学把听到的数减去1报出答案.
概括
问题情境、学生活动
如果第一个同学所报的数为5,我们只需按照左图中的程序做下去,不难发现第四位同学的答案.
实际上,这是在用具体的数来代替最后一个式子
中的字母
,然后算出结果:
即当x=5时,
探索新知
概念
一般地,用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值.
数学应用
例1:当a=2,b=-1,c=-3时,求下列各代数式的值.
⑴b2-4ac;
⑵a2+b2+c2+2ab+2bc+2ac;
⑶(a+b+c)2.
⑴解:当a=2,b=-1,c=-3时
b2-4ac=
(-1)2-4×2×(-3)
=1+24
=25
⑵解:当a=2,b=-1,c=-3时
a2+b2+c2+2ab+2bc+2ac
=22+(-1)2+(-3)2+2×2×(-1)+2×(-1)
×
(-3)+2×2×(-3)
=4+1+9-4+6+12
=4
⑶解:当a=2,b=-1,c=-3时
(a+b+c)2=(2-1-3)2
=4
观察⑵
⑶
两题的结果,你有什么想法?
尝试体验
1.当a=3时,5a=_____;
2.当s=-2时,
2s=_____;
3.当x=
时,
=__;
4.当b=-3时,
=___;
5.当a=2,b=-1时,a-b=__.
15
-4
8
3
1
概念小结
1、求代数式的值的具体步骤,注意点是什么?
①求代数式的值的步骤:
(1)代入,将字母所取的值代入代数式中;
(2)计算,按照代数式指明的运算进行,计算出结果.
②注意的几个问题:
(1)由于代数式的值是由代数式中的字母所取的值确定的,所以代入数值前应先指明字母的取值,把“当……时”写出来;
(2)如果字母的值是负数、分数,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号.
2、口诀:挖去字母变成数,
数字符号全保留,分数负数添括号,运算关系总不变,准确计算不马虎.
数学运用
例2.某企业去年的年产值为a亿元,今年比去年增长了10%。如果明年还能按这个速度增长,请你预测一下,该企业明年的年产值能达到多少亿元?如果去年的年产值是2亿元,那么预计明年的年产值是多少亿元?
解:由题意可得,今年的年产值为
亿元
(1+10%)a
于是明年的年产值为
a(1+10%)(1+10%)=1.21a
若去年的年产值为2亿元,则明年的年产值为
1.21a=1.21×2=2.42(亿元).
答:该企业明年的年产值将能达到1.21a亿元。由去年的年产值是2亿元,可以预测明年的年产值是2.42亿元.
1.按右边图示的程序计算,若开始输入的n值为2,则最后输出的结果是
.
231
输入n
计算
的值
>200
输出结果
yes
no
巩固提升
(逆用乘法分配律)
数学应用
例3:若x+2y2+5的值为7,求代数式3x+6y2+4的值.
解:∵
x+2y2+5=7
∴x+2y2=2
∴
3x+6y2+4
=3(x+2y2)
+4
=3×2+4
=10
1、根据下列各组x、y
的值,分别求出代数式x2
+2xy+y2
与
x2
-2xy+y2
的值:(1)x=2,y=3;(2)x=-2,y=-4.
解:
(1)当x=2,y=3时,
x2
+2xy+y2=22+2×2×3+32
=4+12+9=25
x2
-2xy+y2=22-2×2×3+32
=4-12+9
=1
数学应用
练一练
(2)当x=-2,y=-4时,
x2
+2xy+y2=(-2)2+2×(-2)
×
(-4)
+(-4)2
=4+16+16
=36
x2
-2xy+y2=(-2)2-2×(-2)
×
(-4)
+(-4)2
=4-16+16
=4
数学应用
回顾反思(小结)
1、求代数式的值的步骤:
2、求代数式的值的注意事项:
(1)代入数值前应先指明字母的取值,把“当……时”写出来;
(2)如果字母的值是负数、分数,并且要计算它的乘方,代入时应加上括号;
(3)代数式中省略了乘号时,代入数值以后必须添上乘号;
3、相同的代数式可以看作一个字母——整体代换;
4、代数式的值的广泛应用:计算机编程(包括用
Excel处理数据等)、经济、生活等方面的应用.
(1)代入,(2)计算;
现有两个代数式:3x+1…(1)
…(2)如果随意给出一个正整数,记为x,那么利用这个正整数,我们都可以根据代数式(1)或(2)求出一个对应值.
我们约定一个规则:若正整数x为奇数,我们就根据(1)式求对应值;若正整数x为偶数,我们就根据
(2)式求对应值.例如根据这种规则,若取正整数x为18(偶数),则由(2)式求得对应值为9;而正整数9(奇数),由(1)式求得对应值为28;同样,正整数28(偶数)对应14…我们感兴趣的是,从某一个正整数出发,不断地这样对应下去,会是一个什么样的结果呢?也许这是一个非常吸引人的数学游戏.
思考:有趣的“3x+1”问题
下面我们以正数18为例,不断地做下去,如下图所示,最后竟出现了一个循环:4,2,1,4,2,1,…….
9
18
28
14
7
22
11
20
40
13
26
52
17
34
10
5
16
8
4
2
1
再取一个奇数试试看。比如取x为21,如下图所示,结果是一样的——仍是一个同样的循环.
16
8
4
2
1
21
32
64
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
