2021-2022学年高一上学期数学北师大版(2019)必修第一册6.2.1简单随机抽样习题课 课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版(2019)必修第一册6.2.1简单随机抽样习题课 课件(共34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
习题课
6.2.1简单随机抽样
北师大(2019)必修1
看看这一节我们要学什么
学习目标
1.理解简单随机抽样的定义、特点及适用范围.(重点)
2.掌握两种简单随机抽样的步骤,并能用简单随机抽样方法抽取样本.(难点)
核
心
素
养
1.通过抽取样本,培养数据分析素养.
2.借助简单随机抽样的定义,培养数学抽象素养.
环节一
复习
1.简单随机抽样的定义
一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样.这样抽取的样本,叫做简单随机样本.
2.简单随机抽样的方法
(1)抽签法:
把总体中的N个个体编号,把号码写在号签上,将号签放在一个容器中,搅拌均匀后,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本.
(2)随机数法:
随机抽样中,另一个经常被采用的方法是随机数法,即利用随机数表、随机数骰子或计算机产生的随机数进行抽样.
3.抽签法和随机数法的特点
?
优点
缺点
抽签法
简单易行,当总体的个体数不多时,使总体处于“搅拌”均匀的状态比较容易,这时,每个个体都有均等的机会被抽中,从而能够保证样本的代表性
仅适用于个体数较少的总体,当总体容量较大时,费时费力又不方便,况且,如果号签搅拌的不均匀,可能导致抽样不公平
随机
数法
操作简单易行,它很好地解决了用抽签法当总体中的个数较多时制签难的问题,在总体容量不大的情况下是行之有效的
如果总体中的个体数很多,对个体编号的工作量太大,即使用随机数表法操作也不方便快捷
环节二
理论板块专题
1.对于简单随机抽样,下列说法中正确的是( )
①它要求被抽取样本的总体的个数有限,以便对其中各个个体被抽取的概率进行分析;
②它是从总体中逐个进行抽取,以便在抽样实践中进行操作;
③它是一种不放回抽样;
④它是一种等概率抽样,不仅每次从总体中抽取一个个体时,各个个体被抽取的概率相等,而且在整个抽样过程中,各个个体被抽取的概率也相等,从而保证了这种抽样方法的公平性.
A.①②③
B.①②④
C.①③④
D.①②③④
2.
简单随机抽样的结果( )
A.完全由抽样方式所决定
B.完全由随机性所决定
C.完全由人为因素所决定
D.完全由计算方法所决定
解析:选B 据简单随机抽样的定义,总体中每个个体被抽到的机会相等,因此简单随机抽样的结果只与随机性有关.故选B.
3.下列抽取样本的方式属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后再把它放回盒子里
③从8台电脑中不放回地随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.①
B.②
C.③
D.以上都不对
解析:①不符合简单随机抽样中个体数是有限的特点;②是有放回的抽样,而简单随机抽样是无放回的;③符合简单随机抽样的特点,所以是简单随机抽样.答案:C
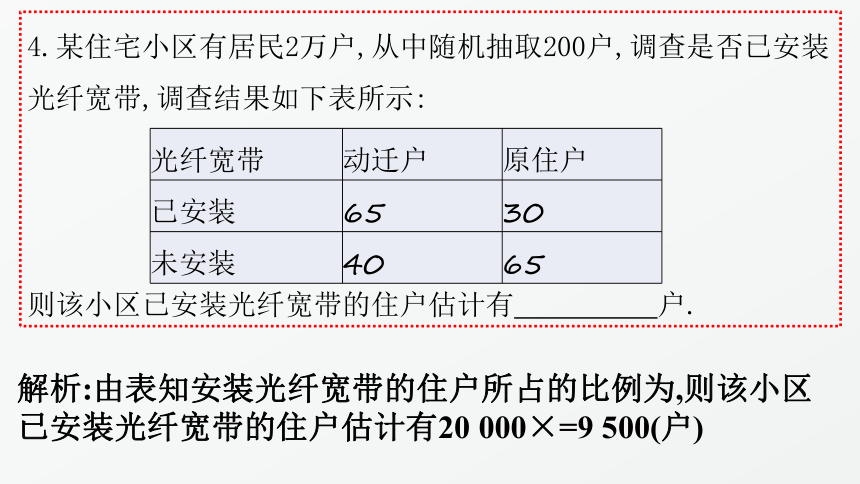
4.某住宅小区有居民2万户,从中随机抽取200户,调查是否已安装光纤宽带,调查结果如下表所示:
则该小区已安装光纤宽带的住户估计有 户.
光纤宽带
动迁户
原住户
已安装
65
30
未安装
40
65
解析:由表知安装光纤宽带的住户所占的比例为,则该小区已安装光纤宽带的住户估计有20
000×=9
500(户)
5.
采用简单随机抽样从含10个个体的总体中抽取一个容量为4的样本,若个体a前两次未被抽到,则第三次被抽到的概率为
解析:第三次被抽到与第一次被抽到的概率相等.
6.
一个总体中共有100个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被抽到的可能性是( )
A.
B.
C.
D.不确定
解析:选B 每个个体被抽到的可能性都是=,故选B.
7.
某年级文科班4个班级,每班各有40名学生(其中男生8人,女生32人).若从该年级文科生中以简单随机抽样抽出20人,则下列选项中正确的是( )
A.每班至少会有一人被抽中
B.抽出来的女生人数一定比男生人数多
C.已知小文是男生,小美是女生,则小文被抽中的可能性小于小美被抽中的可能性
D.若学生甲和学生乙在同一个班,学生丙在另外一个班,则甲、乙两人同时被抽中的可能性跟甲、丙两人同时被抽中的可能性一样
解析:选D 在抽样过程中,每个个体被抽到的可能性都相等,从该年级文科生中以简单随机抽样抽出20人,所有班的学生被抽到的可能性都一样,男生、女生被抽到的可能性都一样,其中任何两人被同时抽到的可能性一样,故选D.
8.
从个体数为N的总体中抽取一个样本容量是30的样本,每个个体被抽到的可能性是,则N的值是________.
解析:从个体数为N的总体中抽出一个样本容量是30的样本,所以每个个体被抽取的可能性是30N.因为每个个体被抽取的可能性是15,所以30N=,所以N=150.
答案:150
9.
某中学高一年级有400人,高二年级有320人,高三年级有280人,以每人被抽取的可能性为0.2,向该中学抽取了一个容量为n的样本,则n=________.
解析:由=0.2,得n=200.
答案:200
10.用简单随机抽样的方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个个体a“第一次被抽到的概率”,“第二次被抽到的概率”,“在整个抽样过程中被抽到的概率”分别是________.
解析:从6个个体中抽1个个体,每个个体被抽到的概率均为,与抽取的次数无关,第二次被抽到的概率仍为.但由于在整个抽样过程中是从6个个体中抽2个样本,故个体a被抽到的概率为.答案:
,
,
环节三
抽签法专题
1.将全班同学按学号编号,制作相应的卡片号签,放入同一个箱子里均匀搅拌,从中抽出15个号签,就相应的15名学生对看足球比赛的喜爱程度(很喜爱、喜爱、一般、不喜爱、很不喜爱)进行调查,使用的是 法.?
解析:抽签法分为编号、制签、取样三步,这里用了学生的学号作为编号,后面的抽取过程符合抽签法的实施步骤,所以采用的是抽签法.
答案:抽签
2.
某种福利彩票的中奖号码是从1~36个号码中,选出7个号码来按规则确定中奖情况,这种从36个号码中选7个号码的抽样方法是________.
解析:符合抽签法的特点:①个体数较少;②样本容量小.
答案:抽签法
3.
一个总体含有100个个体,以简单随机抽样的方式从该总体中抽取一个容量为5的样本,用抽签法抽样的编号一般为________
解析:0,1,…,99(或1,2,…,100)
4.
抽签法中确保样本代表性的关键是( )
A.制签
B.搅拌均匀
C.逐一抽取
D.抽取不放回
B 逐一抽取、抽取不放回是简单随机抽样的特点,但不是确保代表性的关键,一次抽取与有放回抽取(个体被重复取出可不算再放回)也不影响样本的代表性,制签也一样.
环节四
随机数表法专题
1.用随机数表法进行抽样有以下几个步骤:①将总体中的个体编号;②获取样本号码;③选定开始的数字.这些步骤的先后顺序应为( )
A.①②③
B.③②①
C.①③②
D.③①②
解析:随机数表法的步骤可以分为编号、定起点、取号、取样,所以本题的顺序应该是①③②.
答案:C
2.
某工厂的质检人员对生产的100件产品,采用随机数法抽取10件检查,对100件产品采用下面的编号方法
①1,2,3,…,100;②001,002,…,100;③00,01,02…,99;④01,02,03,…,100.
其中正确的序号是( )
A.②③④
B.③④
C.②③
D.①②
解析:选C 根据随机数法的步骤可知,①④编号位数不统一.
3.
已知总体容量为107,若用随机数表法抽取一个容量为10的样本.下面对总体的编号最方便的是( )
A.1,2,…107
B.0,1,2,…,106
C.00,01,…,106
D.000,001,…,106
4.假设要考察某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取6袋进行检验,利用随机数表法抽取样本时,先将500袋牛奶按000,001,…,499进行编号,使用下面随机数表中各个5位数组的后3位,选定第7行第5组数开始,取出047作为抽取的代号,继续向右读,随后检验的5袋牛奶的号码是(下面摘取了某随机数表第7行至第9行)( )
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
A.245,331,421,025,016
B.025,016,105,185,395
C.395,016,245,331,185
D.447,176,335,025,212
5.为了了解高一(10)班53名同学的牙齿健康状况,需从中抽取10名同学做医学检验,现已对53名同学编号为00,01,02,…,50,51,52.从下面所给的随机数表的第1行第3列的5开始从左向右读下去,则选取的号码依次为多少?
随机数表如下:
0154 3287 6595 4287 5346
7953 2586 5741 3369 8324
4597 7386 5244 3578 6241
解:从数5开始从左向右读下去,两位两位地读,把在00~52范围内且前面没出现过的数记下,否则跳过,直到取满10人为止.如下表:
01
54 32
87 65
95 42
87 53
46
79
53 25
86 57
41 33
69 83
24
45
97 73
86 52
44 35
78 62
41
选取的号码依次为32,42,46,25,41,33,24,45,52,44.
6.
总体由编号为00,01,02,…,48,49的50个个体组成,利用随机数表选取8个个体,选取方法是从随机数表的第1行的第9列和第10列数字开始由左到右依次选取两个数字,则选出来的第8个个体的编号为( )
附:第1行至第4行的随机数表
2635 7900 3370 9160 1620 3882 7757 4950
3211 4919 7306 4916 7677 8733 9974 6732
2748 6198 7164 4148 7086 2888 8519 1620
7477 0111 1630 2404 2979 7991 9683 5125
A.16
B.19
C.20
D.38
解析:选B 从随机数表第1行的第9列和第10列数字开始由左到右依次选取两个数字,符合条件的依次为33,16,20,38,49,32,11,19,故第8个数为19.故选B.
6.假设要抽查某种品牌的850颗种子的发芽率,抽取60颗进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第22列的数3开始向右读,请你依次写出最先检测的4颗种子的编号________.(下面摘取了随机数表第7行至第11行)
84
42
17
53
31 57
24
55
06
88 77
04
74
47
67
21
76
33
50
25 83
92
12
06
76 63
01
63
78
59
16
95
55
67
19 98
10
50
71
75 12
86
73
58
07
44
39
52
38
79 33
21
12
34
29 78
64
56
07
82
52
42
07
44
38 15
51
00
13
42 99
66
02
79
54
解析:从第8行第22列的数3开始向右读第一个小于850的数字是301,第二个数字是637,也符合题意,第三个数字是859,大于850,舍去,第四个数字是169,符合题意,第五个数字是555,符合题意,故答案301,637,169,555.
答案:301,637,169,555
7.
为了了解某班学生的身高情况,决定从50名同学中选取10名进行检测(已编号为00~49),利用随机数法进行抽取,得到如下3组编号,正确的是( )
①26,94,29,27,43,99,55,19,81,06;
②20,26,31,40,24,36,19,34,03,48;
③04,00,45,32,44,22,04,11,08,49.
A.①
B.②
C.③
D.②③
解析:选B 获取的样本号码应跳过不在样本编号内的号码,并应去掉重复号码.由此判断②正确,故选B.
8.
总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08
B.07
C.02
D.01
解析:选D 从第1行第5列的数字6开始由左到右依次选出08,02,14,07,01,所以选出来的第5个个体的编号为01.
9.高一(1)班有60名学生,学号从01到60,数学老师在上统计课时,利用随机数法选5名学生提问,老师首先选定从随机数表的倒数第5行(下表为随机数表的最后5行)第6列的“1”开始,向右读依次选学号提问,则被提问的5个学生的学号为________.
8
5
7
0 2
1
5
0 8
1
4
0 4
3
5
5 5
3
2
1 2
5
4
8 0
2
0
8 7
5
4
3
9
1
6
9 0
4
0
8 4
3
5
3 6
1
2
2 8
9
1
3 9
9
3
0 4
1
6
9 6
0
3
2
2
1
2
7 0
1
6
2 6
1
7
6 4
9
6
9 8
1
8
5 9
3
1
2 8
7
4
8 8
5
7
5
8
0
9
0 9
8
7
2 1
9
6
8 0
2
6
3 0
0
8
1 2
6
6
2 6
8
3
1 3
1
0
6
2
9
5
9 9
0
1
1 1
4
4
8 4
3
4
6 7
0
1
9 8
1
4
8 1
5
5
7 8
4
0
0
解析:依据选号规则,选取的5名学生的学号依次为:15,08,14,04,35.
答案:15,08,14,04,35
10.某学校为了调查学生的学习情况,由每班随机抽取5名学生进行调查,若(1)班有50名学生,将每一名学生编号,从01到50止.请从下面提供的随机数表的第2行第6列开始,依次向右,直到取足样本,则抽取样本的号码是________.
03 47 43 73 86 39 96 47 36 61 46 98
63 71 62 33 26 16 80 45 60 11 14 10
95 91 74 24 67 62 42 81 14 57 20 42
53 32 37 32 27 07 36 07 51 24 51 79
解析:依据随机数表可得所抽取的样本的号码分别为23,32,04,01,11.
答案:23,32,04,01,11
习题课
6.2.1简单随机抽样
北师大(2019)必修1
看看这一节我们要学什么
学习目标
1.理解简单随机抽样的定义、特点及适用范围.(重点)
2.掌握两种简单随机抽样的步骤,并能用简单随机抽样方法抽取样本.(难点)
核
心
素
养
1.通过抽取样本,培养数据分析素养.
2.借助简单随机抽样的定义,培养数学抽象素养.
环节一
复习
1.简单随机抽样的定义
一般地,设一个总体含有N个个体,从中逐个不放回地抽取n个个体作为样本(n≤N),如果每次抽取时总体内的各个个体被抽到的机会都相等,就把这种抽样方法叫做简单随机抽样.这样抽取的样本,叫做简单随机样本.
2.简单随机抽样的方法
(1)抽签法:
把总体中的N个个体编号,把号码写在号签上,将号签放在一个容器中,搅拌均匀后,每次从中抽取一个号签,连续抽取n次,就得到一个容量为n的样本.
(2)随机数法:
随机抽样中,另一个经常被采用的方法是随机数法,即利用随机数表、随机数骰子或计算机产生的随机数进行抽样.
3.抽签法和随机数法的特点
?
优点
缺点
抽签法
简单易行,当总体的个体数不多时,使总体处于“搅拌”均匀的状态比较容易,这时,每个个体都有均等的机会被抽中,从而能够保证样本的代表性
仅适用于个体数较少的总体,当总体容量较大时,费时费力又不方便,况且,如果号签搅拌的不均匀,可能导致抽样不公平
随机
数法
操作简单易行,它很好地解决了用抽签法当总体中的个数较多时制签难的问题,在总体容量不大的情况下是行之有效的
如果总体中的个体数很多,对个体编号的工作量太大,即使用随机数表法操作也不方便快捷
环节二
理论板块专题
1.对于简单随机抽样,下列说法中正确的是( )
①它要求被抽取样本的总体的个数有限,以便对其中各个个体被抽取的概率进行分析;
②它是从总体中逐个进行抽取,以便在抽样实践中进行操作;
③它是一种不放回抽样;
④它是一种等概率抽样,不仅每次从总体中抽取一个个体时,各个个体被抽取的概率相等,而且在整个抽样过程中,各个个体被抽取的概率也相等,从而保证了这种抽样方法的公平性.
A.①②③
B.①②④
C.①③④
D.①②③④
2.
简单随机抽样的结果( )
A.完全由抽样方式所决定
B.完全由随机性所决定
C.完全由人为因素所决定
D.完全由计算方法所决定
解析:选B 据简单随机抽样的定义,总体中每个个体被抽到的机会相等,因此简单随机抽样的结果只与随机性有关.故选B.
3.下列抽取样本的方式属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后再把它放回盒子里
③从8台电脑中不放回地随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.①
B.②
C.③
D.以上都不对
解析:①不符合简单随机抽样中个体数是有限的特点;②是有放回的抽样,而简单随机抽样是无放回的;③符合简单随机抽样的特点,所以是简单随机抽样.答案:C
4.某住宅小区有居民2万户,从中随机抽取200户,调查是否已安装光纤宽带,调查结果如下表所示:
则该小区已安装光纤宽带的住户估计有 户.
光纤宽带
动迁户
原住户
已安装
65
30
未安装
40
65
解析:由表知安装光纤宽带的住户所占的比例为,则该小区已安装光纤宽带的住户估计有20
000×=9
500(户)
5.
采用简单随机抽样从含10个个体的总体中抽取一个容量为4的样本,若个体a前两次未被抽到,则第三次被抽到的概率为
解析:第三次被抽到与第一次被抽到的概率相等.
6.
一个总体中共有100个个体,用简单随机抽样的方法从中抽取一个容量为20的样本,则某一特定个体被抽到的可能性是( )
A.
B.
C.
D.不确定
解析:选B 每个个体被抽到的可能性都是=,故选B.
7.
某年级文科班4个班级,每班各有40名学生(其中男生8人,女生32人).若从该年级文科生中以简单随机抽样抽出20人,则下列选项中正确的是( )
A.每班至少会有一人被抽中
B.抽出来的女生人数一定比男生人数多
C.已知小文是男生,小美是女生,则小文被抽中的可能性小于小美被抽中的可能性
D.若学生甲和学生乙在同一个班,学生丙在另外一个班,则甲、乙两人同时被抽中的可能性跟甲、丙两人同时被抽中的可能性一样
解析:选D 在抽样过程中,每个个体被抽到的可能性都相等,从该年级文科生中以简单随机抽样抽出20人,所有班的学生被抽到的可能性都一样,男生、女生被抽到的可能性都一样,其中任何两人被同时抽到的可能性一样,故选D.
8.
从个体数为N的总体中抽取一个样本容量是30的样本,每个个体被抽到的可能性是,则N的值是________.
解析:从个体数为N的总体中抽出一个样本容量是30的样本,所以每个个体被抽取的可能性是30N.因为每个个体被抽取的可能性是15,所以30N=,所以N=150.
答案:150
9.
某中学高一年级有400人,高二年级有320人,高三年级有280人,以每人被抽取的可能性为0.2,向该中学抽取了一个容量为n的样本,则n=________.
解析:由=0.2,得n=200.
答案:200
10.用简单随机抽样的方法从含有6个个体的总体中,抽取一个容量为2的样本,某一个个体a“第一次被抽到的概率”,“第二次被抽到的概率”,“在整个抽样过程中被抽到的概率”分别是________.
解析:从6个个体中抽1个个体,每个个体被抽到的概率均为,与抽取的次数无关,第二次被抽到的概率仍为.但由于在整个抽样过程中是从6个个体中抽2个样本,故个体a被抽到的概率为.答案:
,
,
环节三
抽签法专题
1.将全班同学按学号编号,制作相应的卡片号签,放入同一个箱子里均匀搅拌,从中抽出15个号签,就相应的15名学生对看足球比赛的喜爱程度(很喜爱、喜爱、一般、不喜爱、很不喜爱)进行调查,使用的是 法.?
解析:抽签法分为编号、制签、取样三步,这里用了学生的学号作为编号,后面的抽取过程符合抽签法的实施步骤,所以采用的是抽签法.
答案:抽签
2.
某种福利彩票的中奖号码是从1~36个号码中,选出7个号码来按规则确定中奖情况,这种从36个号码中选7个号码的抽样方法是________.
解析:符合抽签法的特点:①个体数较少;②样本容量小.
答案:抽签法
3.
一个总体含有100个个体,以简单随机抽样的方式从该总体中抽取一个容量为5的样本,用抽签法抽样的编号一般为________
解析:0,1,…,99(或1,2,…,100)
4.
抽签法中确保样本代表性的关键是( )
A.制签
B.搅拌均匀
C.逐一抽取
D.抽取不放回
B 逐一抽取、抽取不放回是简单随机抽样的特点,但不是确保代表性的关键,一次抽取与有放回抽取(个体被重复取出可不算再放回)也不影响样本的代表性,制签也一样.
环节四
随机数表法专题
1.用随机数表法进行抽样有以下几个步骤:①将总体中的个体编号;②获取样本号码;③选定开始的数字.这些步骤的先后顺序应为( )
A.①②③
B.③②①
C.①③②
D.③①②
解析:随机数表法的步骤可以分为编号、定起点、取号、取样,所以本题的顺序应该是①③②.
答案:C
2.
某工厂的质检人员对生产的100件产品,采用随机数法抽取10件检查,对100件产品采用下面的编号方法
①1,2,3,…,100;②001,002,…,100;③00,01,02…,99;④01,02,03,…,100.
其中正确的序号是( )
A.②③④
B.③④
C.②③
D.①②
解析:选C 根据随机数法的步骤可知,①④编号位数不统一.
3.
已知总体容量为107,若用随机数表法抽取一个容量为10的样本.下面对总体的编号最方便的是( )
A.1,2,…107
B.0,1,2,…,106
C.00,01,…,106
D.000,001,…,106
4.假设要考察某企业生产的袋装牛奶的质量是否达标,现从500袋牛奶中抽取6袋进行检验,利用随机数表法抽取样本时,先将500袋牛奶按000,001,…,499进行编号,使用下面随机数表中各个5位数组的后3位,选定第7行第5组数开始,取出047作为抽取的代号,继续向右读,随后检验的5袋牛奶的号码是(下面摘取了某随机数表第7行至第9行)( )
84421 75331 57245 50688 77047 44767 21763
35025 83921 20676 63016 47859 16955 56719
98105 07185 12867 35807 44395 23879 33211
A.245,331,421,025,016
B.025,016,105,185,395
C.395,016,245,331,185
D.447,176,335,025,212
5.为了了解高一(10)班53名同学的牙齿健康状况,需从中抽取10名同学做医学检验,现已对53名同学编号为00,01,02,…,50,51,52.从下面所给的随机数表的第1行第3列的5开始从左向右读下去,则选取的号码依次为多少?
随机数表如下:
0154 3287 6595 4287 5346
7953 2586 5741 3369 8324
4597 7386 5244 3578 6241
解:从数5开始从左向右读下去,两位两位地读,把在00~52范围内且前面没出现过的数记下,否则跳过,直到取满10人为止.如下表:
01
54 32
87 65
95 42
87 53
46
79
53 25
86 57
41 33
69 83
24
45
97 73
86 52
44 35
78 62
41
选取的号码依次为32,42,46,25,41,33,24,45,52,44.
6.
总体由编号为00,01,02,…,48,49的50个个体组成,利用随机数表选取8个个体,选取方法是从随机数表的第1行的第9列和第10列数字开始由左到右依次选取两个数字,则选出来的第8个个体的编号为( )
附:第1行至第4行的随机数表
2635 7900 3370 9160 1620 3882 7757 4950
3211 4919 7306 4916 7677 8733 9974 6732
2748 6198 7164 4148 7086 2888 8519 1620
7477 0111 1630 2404 2979 7991 9683 5125
A.16
B.19
C.20
D.38
解析:选B 从随机数表第1行的第9列和第10列数字开始由左到右依次选取两个数字,符合条件的依次为33,16,20,38,49,32,11,19,故第8个数为19.故选B.
6.假设要抽查某种品牌的850颗种子的发芽率,抽取60颗进行实验.利用随机数表抽取种子时,先将850颗种子按001,002,…,850进行编号,如果从随机数表第8行第22列的数3开始向右读,请你依次写出最先检测的4颗种子的编号________.(下面摘取了随机数表第7行至第11行)
84
42
17
53
31 57
24
55
06
88 77
04
74
47
67
21
76
33
50
25 83
92
12
06
76 63
01
63
78
59
16
95
55
67
19 98
10
50
71
75 12
86
73
58
07
44
39
52
38
79 33
21
12
34
29 78
64
56
07
82
52
42
07
44
38 15
51
00
13
42 99
66
02
79
54
解析:从第8行第22列的数3开始向右读第一个小于850的数字是301,第二个数字是637,也符合题意,第三个数字是859,大于850,舍去,第四个数字是169,符合题意,第五个数字是555,符合题意,故答案301,637,169,555.
答案:301,637,169,555
7.
为了了解某班学生的身高情况,决定从50名同学中选取10名进行检测(已编号为00~49),利用随机数法进行抽取,得到如下3组编号,正确的是( )
①26,94,29,27,43,99,55,19,81,06;
②20,26,31,40,24,36,19,34,03,48;
③04,00,45,32,44,22,04,11,08,49.
A.①
B.②
C.③
D.②③
解析:选B 获取的样本号码应跳过不在样本编号内的号码,并应去掉重复号码.由此判断②正确,故选B.
8.
总体由编号为01,02,…,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行第5列的数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
A.08
B.07
C.02
D.01
解析:选D 从第1行第5列的数字6开始由左到右依次选出08,02,14,07,01,所以选出来的第5个个体的编号为01.
9.高一(1)班有60名学生,学号从01到60,数学老师在上统计课时,利用随机数法选5名学生提问,老师首先选定从随机数表的倒数第5行(下表为随机数表的最后5行)第6列的“1”开始,向右读依次选学号提问,则被提问的5个学生的学号为________.
8
5
7
0 2
1
5
0 8
1
4
0 4
3
5
5 5
3
2
1 2
5
4
8 0
2
0
8 7
5
4
3
9
1
6
9 0
4
0
8 4
3
5
3 6
1
2
2 8
9
1
3 9
9
3
0 4
1
6
9 6
0
3
2
2
1
2
7 0
1
6
2 6
1
7
6 4
9
6
9 8
1
8
5 9
3
1
2 8
7
4
8 8
5
7
5
8
0
9
0 9
8
7
2 1
9
6
8 0
2
6
3 0
0
8
1 2
6
6
2 6
8
3
1 3
1
0
6
2
9
5
9 9
0
1
1 1
4
4
8 4
3
4
6 7
0
1
9 8
1
4
8 1
5
5
7 8
4
0
0
解析:依据选号规则,选取的5名学生的学号依次为:15,08,14,04,35.
答案:15,08,14,04,35
10.某学校为了调查学生的学习情况,由每班随机抽取5名学生进行调查,若(1)班有50名学生,将每一名学生编号,从01到50止.请从下面提供的随机数表的第2行第6列开始,依次向右,直到取足样本,则抽取样本的号码是________.
03 47 43 73 86 39 96 47 36 61 46 98
63 71 62 33 26 16 80 45 60 11 14 10
95 91 74 24 67 62 42 81 14 57 20 42
53 32 37 32 27 07 36 07 51 24 51 79
解析:依据随机数表可得所抽取的样本的号码分别为23,32,04,01,11.
答案:23,32,04,01,11
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
