1.2.2矩形的判定 课件(共26张PPT)
文档属性
| 名称 | 1.2.2矩形的判定 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 22:38:53 | ||
图片预览








文档简介
(共26张PPT)
导入新课
问题1
矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2
矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
1.2
矩形的性质与判定
第2课时
矩形的判定
学习目标
1.经历矩形判定定理的猜想与证明过程,理解并掌握
矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.
(难点)
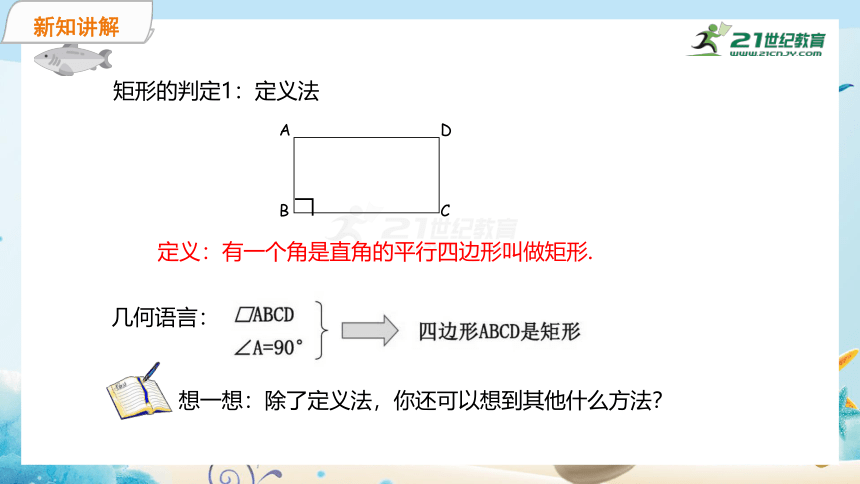
矩形的判定1:定义法
D
B
C
A
∟
定义:有一个角是直角的平行四边形叫做矩形.
几何语言:
想一想:除了定义法,你还可以想到其他什么方法?
新知讲解
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
新知讲解
如图是一个平行四边形的活动框架.
拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
答:随着∠α
的增大,两条对角线的长度将慢慢的变成相等的
(2)当两条对角线的长度相等时,平行四边形又什么特征?由此你能得到一个怎样的猜想?
新知讲解
猜想:“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩
形。”
新知讲解
已知:如图,在
ABCD中,AC、BD是它的两条对角线,AC=BD.
求证:
ABCD是矩形.
证明:
∵四边形ABCD是平行四边形.
∴AB=CD,AB∥CD.
又∵AC=DB,BC=CB.
∴
△ABC≌△DCB.
∴∠ABC=∠DCB.
又∵AB∥CD.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB
=
×180°=90°.
∴
ABCD是矩形.(矩形的定义)
新知讲解
矩形的判定2:对角线相等的平行四边形是矩形
几何语言:
D
B
C
A
O
在□ABCD中
AC=BD
新知讲解
小明同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形?
你能证明上述结论吗?
新知讲解
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
D
B
C
A
∴四边形ABCD是矩形.
新知讲解
矩形的判定3:三个角是直角的四边形是矩形.
几何语言:
D
B
C
A
O
在□ABCD中
∠A=∠B=∠C=90°
新知讲解
典例解析
例1
如图,在
ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC=
AC,
OB=OD=
BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例2
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵
AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
练一练
1.如图,在?ABCD中,AC和BD相交于点O,则下面条件能判定?ABCD是矩形的是
( )
A.AC=BD
B.AC=BC
C.AD=BC
D.AB=AD
A
2.如图
ABCD中,
∠1=
∠2中.此时四边形ABCD是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴
AO=CO,DO=BO.
又∵
∠1=
∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形.
例3
如图,
□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形
EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴
∠BAE+
∠ABF=
∠DAB+
∠ABC=90°.
例4
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=
∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=
∠CAM,
∴∠DAE=∠DAC+∠CAE
=
(∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
1.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是 ( )
A.AB=AD
B.OA=OB
C.AC=BD
D.DC⊥BC
【解析】选A.当DC⊥BC时,根据有一个角是直角的平行四边形是矩形可证四边形ABCD是矩形;当OA=OB或AC=BD时,根据对角线相等的四边形是矩形可证四边形ABCD为矩形;当AB=AD时,可证四边形ABCD为菱形,不能证四边形ABCD为矩形.故选A.
A
课堂练习
【解析】∵∠C=90°,EF⊥AC,EG⊥BC,
∴∠C=∠EFC=∠EGC=90°,
∴四边形FCGE是矩形,
∴FC=EG,FE=CG,EF∥CG,EG∥CA,
∴∠BEG=∠A=45°=∠B,
∴EG=BG,
同理AF=EF,
∴矩形CFEG的周长是CF+EF+EG+CG=CF+AF+BG+CG=AC+BC=6+6=12.
2.如图,Rt△ABC中,∠C=90°,AC=BC=6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则四边形CFEG的周长是
.2·1·c·n·j·y
12
课堂练习
3.矩形的一边长为6,各边中点围成的四边形的周长是20
,则矩形的对角线为
_______,面积为__________.21c
【解析】如图,四边形ABCD为矩形,∠A=90°,
因为E、F、M、N是AB,AD,BC、CD中点,所以EFNM是菱形,
因为周长为20,所以EF=5,AB=6,AE=3,
在RT△AEF中,利用勾股定理可得AF=8,则AD=8,
在RT△ABD中,利用勾股定理可得BD=10,所以矩形ABCD的面积=48.
10
48
课堂练习
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M,N分别为BC,AD的中点.
求证:四边形BMDN是矩形.
证明:在正三角形ABD和BCD中,M,N分别为BC,AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.
课堂练习
课堂总结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
导入新课
问题1
矩形的定义是什么?
有一个角是直角的平行四边形叫做矩形.
问题2
矩形有哪些性质?
矩形
边:
角:
对角线:
对边平行且相等
四个角都是直角
对角线互相平分且相等
思考
工人师傅在做门窗或矩形零件时,如何确保图形是矩形呢?现在师傅带了两种工具(卷尺和量角器),他说用这两种工具的任意一种就可以解决问题,这是为什么呢?
这节课我们一起探讨矩形的判定吧.
1.2
矩形的性质与判定
第2课时
矩形的判定
学习目标
1.经历矩形判定定理的猜想与证明过程,理解并掌握
矩形的判定定理.(重点)
2.能应用矩形的判定解决简单的证明题和计算题.
(难点)
矩形的判定1:定义法
D
B
C
A
∟
定义:有一个角是直角的平行四边形叫做矩形.
几何语言:
想一想:除了定义法,你还可以想到其他什么方法?
新知讲解
工人师傅为了检验两组对边相等的四边形窗框是否成矩形,一种方法是量一量这个四边形的两条对角线长度,如果对角线长相等,则窗框一定是矩形,你知道为什么吗?
新知讲解
如图是一个平行四边形的活动框架.
拉动一对不相邻的顶点时,平行四边形的形状会发生变化。
(1)随着∠α的变化,两条对角线的长度将发生怎样的变化?
答:随着∠α
的增大,两条对角线的长度将慢慢的变成相等的
(2)当两条对角线的长度相等时,平行四边形又什么特征?由此你能得到一个怎样的猜想?
新知讲解
猜想:“如果一个平行四边形的两条对角线相等,那么这个平行四边形是一个矩
形。”
新知讲解
已知:如图,在
ABCD中,AC、BD是它的两条对角线,AC=BD.
求证:
ABCD是矩形.
证明:
∵四边形ABCD是平行四边形.
∴AB=CD,AB∥CD.
又∵AC=DB,BC=CB.
∴
△ABC≌△DCB.
∴∠ABC=∠DCB.
又∵AB∥CD.
∴∠ABC+∠DCB=180°.
∴∠ABC=∠DCB
=
×180°=90°.
∴
ABCD是矩形.(矩形的定义)
新知讲解
矩形的判定2:对角线相等的平行四边形是矩形
几何语言:
D
B
C
A
O
在□ABCD中
AC=BD
新知讲解
小明同学用“边——直角、边——直角、边——直角、边”这样四步,画出了一个四边形,她说这就是一个矩形,她的判断对吗?为什么?
猜想:有三个角是直角的四边形是矩形?
你能证明上述结论吗?
新知讲解
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
证明:
∵
∠A=∠B=∠C=90°,
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
求证:四边形ABCD是矩形.
∴四边形ABCD是平行四边形.
D
B
C
A
∴四边形ABCD是矩形.
新知讲解
矩形的判定3:三个角是直角的四边形是矩形.
几何语言:
D
B
C
A
O
在□ABCD中
∠A=∠B=∠C=90°
新知讲解
典例解析
例1
如图,在
ABCD中,对角线AC,BD相交于点O,且OA=OD,∠OAD=50°.求∠OAB的度数.
A
B
C
D
O
解:∵四边形ABCD是平行四边形,
∴OA=OC=
AC,
OB=OD=
BD.
又∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°.
又∵∠OAD=50°,
∴∠OAB=40°.
例2
如图,矩形ABCD的对角线AC、BD相交于点O,E、F、G、H分别是AO、BO、CO、DO上的一点,且AE=BF=CG=DH.求证:四边形EFGH是矩形.
B
C
D
E
F
G
H
O
A
证明:
∵四边形ABCD是矩形,
∴AC=BD(矩形的对角线相等),
AO=BO=CO=DO(矩形的对角线互相平分),
∵
AE=BF=CG=DH,
∴OE=OF=OG=OH,
∴四边形EFGH是平行四边形,
∵EO+OG=FO+OH,
即EG=FH,
∴四边形EFGH是矩形.
练一练
1.如图,在?ABCD中,AC和BD相交于点O,则下面条件能判定?ABCD是矩形的是
( )
A.AC=BD
B.AC=BC
C.AD=BC
D.AB=AD
A
2.如图
ABCD中,
∠1=
∠2中.此时四边形ABCD是矩形吗?为什么?
A
B
C
D
O
1
2
解:四边形ABCD是矩形.
理由如下:
∵四边形ABCD是平行四边形
∴
AO=CO,DO=BO.
又∵
∠1=
∠2,
∴AO=BO,
∴AC=BD,
∴四边形ABCD是矩形.
例3
如图,
□?ABCD的四个内角的平分线分别相交于E、F、G、H,求证:四边形
EFGH为矩形.
证明:在□?ABCD中,AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE与BG分别为∠DAB、
∠ABC的平分线,
A
B
D
C
H
E
F
G
∴四边形EFGH是矩形.
同理可证∠AED=∠EHG=90°,
∴∠AFB=90°,
∴∠GFE=90°.
∴
∠BAE+
∠ABF=
∠DAB+
∠ABC=90°.
例4
如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E,求证:四边形ADCE为矩形.
证明:在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,即∠DAC=
∠BAC.
又∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE=
∠CAM,
∴∠DAE=∠DAC+∠CAE
=
(∠BAC+∠CAM)=90°.
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
1.在□ABCD中,AC交BD于点O,再添加一个条件,仍不能判定四边形ABCD是矩形的是 ( )
A.AB=AD
B.OA=OB
C.AC=BD
D.DC⊥BC
【解析】选A.当DC⊥BC时,根据有一个角是直角的平行四边形是矩形可证四边形ABCD是矩形;当OA=OB或AC=BD时,根据对角线相等的四边形是矩形可证四边形ABCD为矩形;当AB=AD时,可证四边形ABCD为菱形,不能证四边形ABCD为矩形.故选A.
A
课堂练习
【解析】∵∠C=90°,EF⊥AC,EG⊥BC,
∴∠C=∠EFC=∠EGC=90°,
∴四边形FCGE是矩形,
∴FC=EG,FE=CG,EF∥CG,EG∥CA,
∴∠BEG=∠A=45°=∠B,
∴EG=BG,
同理AF=EF,
∴矩形CFEG的周长是CF+EF+EG+CG=CF+AF+BG+CG=AC+BC=6+6=12.
2.如图,Rt△ABC中,∠C=90°,AC=BC=6,E是斜边AB上任意一点,作EF⊥AC于F,EG⊥BC于G,则四边形CFEG的周长是
.2·1·c·n·j·y
12
课堂练习
3.矩形的一边长为6,各边中点围成的四边形的周长是20
,则矩形的对角线为
_______,面积为__________.21c
【解析】如图,四边形ABCD为矩形,∠A=90°,
因为E、F、M、N是AB,AD,BC、CD中点,所以EFNM是菱形,
因为周长为20,所以EF=5,AB=6,AE=3,
在RT△AEF中,利用勾股定理可得AF=8,则AD=8,
在RT△ABD中,利用勾股定理可得BD=10,所以矩形ABCD的面积=48.
10
48
课堂练习
4.已知:如图,四边形ABCD是由两个全等的正三角形ABD和BCD组成的,M,N分别为BC,AD的中点.
求证:四边形BMDN是矩形.
证明:在正三角形ABD和BCD中,M,N分别为BC,AD的中点.
∴BN⊥AD,DM⊥BC,∠DBC=60°,
∠BND=∠DMB=90°,∠NBD=30°.
∴∠NBM=90°.
∴四边形BMDN是矩形.
课堂练习
课堂总结
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形.
有三个角是直角的四边形是矩形.
运用定理进行计算和证明
矩形的判定
定义
判定定理
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
