正方形
图片预览


文档简介
(共24张PPT)
北雅中学 舒美君
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形------------- 有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形。
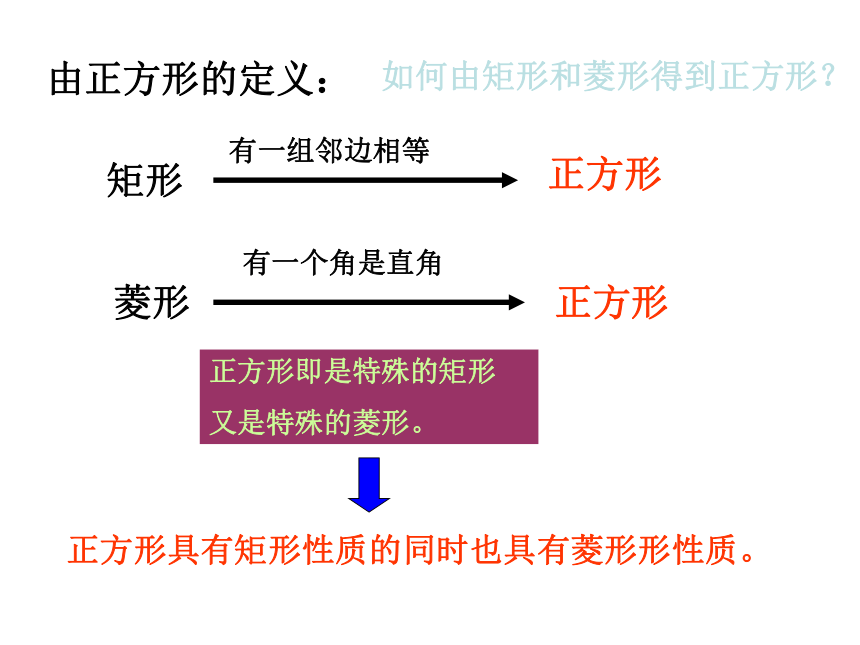
由正方形的定义:
菱形
正方形
有一个角是直角
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质的同时也具有菱形形性质。
正方形
矩形
有一组邻边相等
如何由矩形和菱形得到正方形?
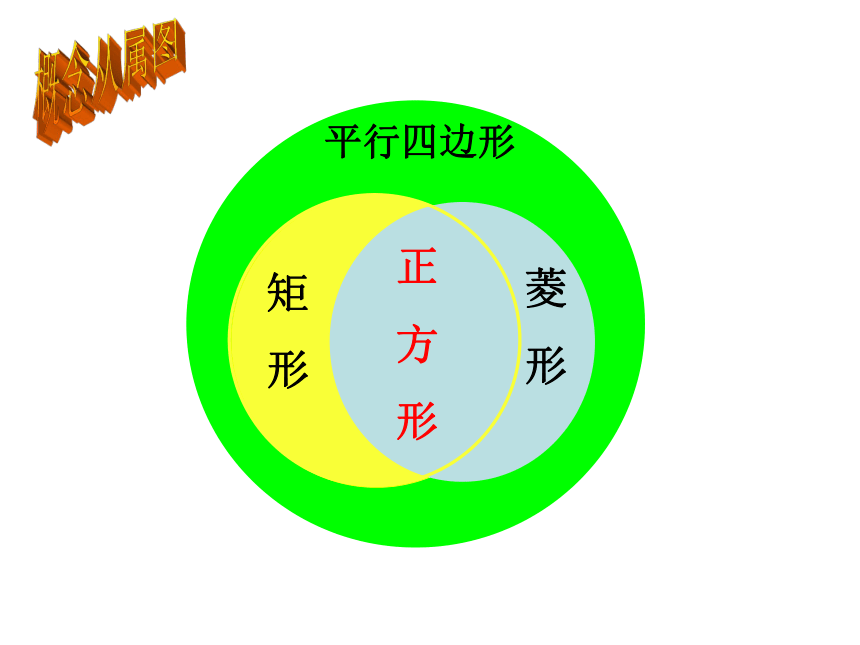
平行四边形
矩
形
菱
形
正
方
形
1.矩形性质
性质回味
答:矩形的4个角都是直角
矩形的对角线相等
2.菱形性质
答:菱形的4条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角.
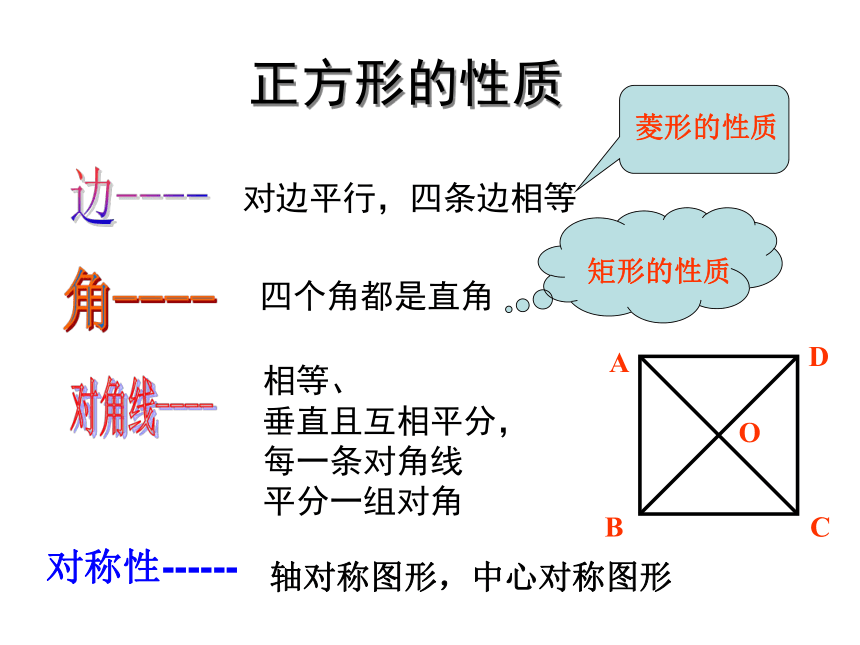
正方形的性质
对边平行,四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
菱形的性质
矩形的性质
对称性------
轴对称图形,中心对称图形
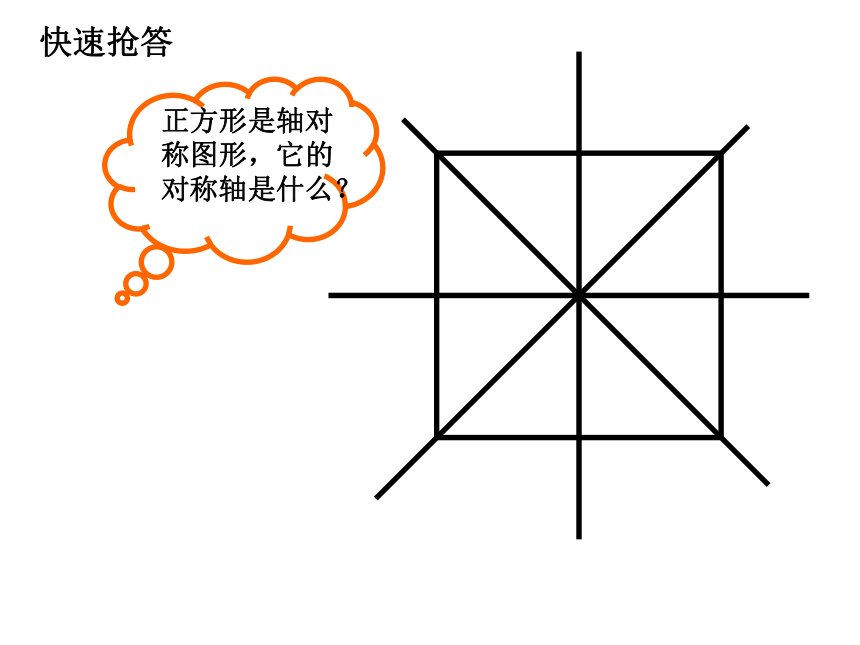
正方形是轴对称图形,它的对称轴是什么?
快速抢答
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
挑战第一关
1.正方形具有而一般矩形不具备的性质是:
2.正方形具有而一般菱形不具备的性质是:
4条边都相等,对角线互相垂直.
4个角都是直角,对角线相等.
3.正方形的周长为12, 则它的对角线长是_____.
4.正方形的面积为12, 则它的边长是_____.
5.正方形对角线长12,则它的面积是_____.
6 .正方形的两条对角线把它分 成_____个全等的____________三角形,此时图中共有___个直角三角形.
72
4
等腰直角
8
挑战第二关
具备什么条件的平行四边形是正方形?
正方形的判别方法:
1.先说明这个平行四边形是矩形,再说明这个矩形也是菱形.
2.先说明这个平行四边形是菱形,再说明这个菱形是矩形.
若前提是平行四边形,该如何说明呢?
若前提是四边形,该如何说明呢?
一般先说明它是平行四边形,然后方法同上.
1.一个矩形的2条对角线互相垂直,这个矩形一定是正方形吗?为什么?
D
O
C
B
A
∵矩形ABCD,AC⊥BD
∴四边形ABCD是正方形
(对角线互相垂直的矩形是正方形)
说说看
2.一个矩形的2条邻边相等,这个矩形一定是正方形吗?为什么?
∵矩形ABCD,AB=AD
∴四边形ABCD是正方形
(有一组邻边相等的矩形是正方形)
4.一个菱形有一个角是直角,它一定是正方形吗?为什么?
说说看
D
O
C
B
A
∵菱形ABCD,∠ABC=90 °
∴四边形ABCD是正方形
(有一个角是直角的菱形是正方形)
3.一个菱形的2条对角线相等,这个菱形一定是正方形吗?为什么?
∵菱形ABCD,AC=BD
∴四边形ABCD是正方形
(对角线相等的菱形是正方形)
已知:正方形ABCD中,点E、F 、 G 、 H分别在AB 、 BC 、 CD 、 DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
试一试
H
G
F
E
D
C
B
A
3
2
1
思路:
①先判定它是菱形:
EF=FG=GH=HE
②再判定它有一个角是90°
理由:
(有一个角是直角的菱形是正方形)
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°,AB=AD=DC=BC(正方形的四条边都相等,四个角都是直角).
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∵ ∠1=∠3.
又 ∠3+∠2=90°
∠1+∠2=90°.
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
试一试
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
.ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
活动
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=50m,EB=30m
∴ S正方形ABCD=(40 )2=1600(m2)
∴
∴
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
我理解了……
我学会了……
……
我知道了……
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
1.已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
北雅中学 舒美君
回顾:特殊的平行四边形
矩形---------------有一个角是直角的平行四边形叫做矩形。
菱形------------- 有一组邻边相等的平行四边形叫做菱形。
有一个角是直角,有一组邻边相等的平行四边形是什么呢?
正方形的定义:
有一组邻边相等并且有一个角是直角的平行四边形。
由正方形的定义:
菱形
正方形
有一个角是直角
正方形即是特殊的矩形
又是特殊的菱形。
正方形具有矩形性质的同时也具有菱形形性质。
正方形
矩形
有一组邻边相等
如何由矩形和菱形得到正方形?
平行四边形
矩
形
菱
形
正
方
形
1.矩形性质
性质回味
答:矩形的4个角都是直角
矩形的对角线相等
2.菱形性质
答:菱形的4条边都相等
菱形的对角线互相垂直,并且每条对角线平分一组对角.
正方形的性质
对边平行,四条边相等
四个角都是直角
相等、
垂直且互相平分,
每一条对角线
平分一组对角
A
B
C
D
O
菱形的性质
矩形的性质
对称性------
轴对称图形,中心对称图形
正方形是轴对称图形,它的对称轴是什么?
快速抢答
例
求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
这是一道文字证明题,该怎么做
第一步:根据题意画出图形
第二步:写出已知、求证
第三步:进行证明
A
D
C
B
O
已知:如图,四边形ABCD是正方形,对 角线AC、BD相交于点O.
求证:△ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO
分析:利用正方形的性质,对角线互相垂直平分且相等,每条对角线平分一组对角.平分可以产生线段等量关系,垂直可以产生直角,于是可以得到四个全等的等腰直角三角形.
A
D
C
B
O
正方形对角线把正方形分成多少个等腰直角三角形?
拓展讨论:
结论:
分成八个等腰直角三角形,分别是△ABC、 △ADC、 △ABD、 △BCD ;
△AOB、 △BOC、 △COD、 △DOA.
挑战第一关
1.正方形具有而一般矩形不具备的性质是:
2.正方形具有而一般菱形不具备的性质是:
4条边都相等,对角线互相垂直.
4个角都是直角,对角线相等.
3.正方形的周长为12, 则它的对角线长是_____.
4.正方形的面积为12, 则它的边长是_____.
5.正方形对角线长12,则它的面积是_____.
6 .正方形的两条对角线把它分 成_____个全等的____________三角形,此时图中共有___个直角三角形.
72
4
等腰直角
8
挑战第二关
具备什么条件的平行四边形是正方形?
正方形的判别方法:
1.先说明这个平行四边形是矩形,再说明这个矩形也是菱形.
2.先说明这个平行四边形是菱形,再说明这个菱形是矩形.
若前提是平行四边形,该如何说明呢?
若前提是四边形,该如何说明呢?
一般先说明它是平行四边形,然后方法同上.
1.一个矩形的2条对角线互相垂直,这个矩形一定是正方形吗?为什么?
D
O
C
B
A
∵矩形ABCD,AC⊥BD
∴四边形ABCD是正方形
(对角线互相垂直的矩形是正方形)
说说看
2.一个矩形的2条邻边相等,这个矩形一定是正方形吗?为什么?
∵矩形ABCD,AB=AD
∴四边形ABCD是正方形
(有一组邻边相等的矩形是正方形)
4.一个菱形有一个角是直角,它一定是正方形吗?为什么?
说说看
D
O
C
B
A
∵菱形ABCD,∠ABC=90 °
∴四边形ABCD是正方形
(有一个角是直角的菱形是正方形)
3.一个菱形的2条对角线相等,这个菱形一定是正方形吗?为什么?
∵菱形ABCD,AC=BD
∴四边形ABCD是正方形
(对角线相等的菱形是正方形)
已知:正方形ABCD中,点E、F 、 G 、 H分别在AB 、 BC 、 CD 、 DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
试一试
H
G
F
E
D
C
B
A
3
2
1
思路:
①先判定它是菱形:
EF=FG=GH=HE
②再判定它有一个角是90°
理由:
(有一个角是直角的菱形是正方形)
已知:正方形ABCD中,点E、F、G 、H分别在AB 、BC 、CD 、DA上,且AE=BF=CG=DH,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
1
2
3
证明:∵ 四边形ABCD是正方形
∴ ∠ABC=∠BCD=90°,AB=AD=DC=BC(正方形的四条边都相等,四个角都是直角).
又∵ AE=BF=CG=DH
∴AB-AE=AD-DH=DC-CG=BC-BF
即BE=AH=DG=CF
∴ △AEH≌△BFE≌ △CGF ≌ △DHG.
∵ ∠1=∠3.
又 ∠3+∠2=90°
∠1+∠2=90°.
∴ 四边形EFGH是正方形(有一个角是直角的菱形是矩形).
试一试
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
.ABCD是一块正方形场地,小华和小芳在AB边上取定了一点E,经测量EC=50m,EB=30m,这块场地的面积和对角线长分别是多少?
A
D
A
B
C
E
活动
解:
连接AC.
∵ 四边形ABCD是正方形
∴ ∠B=90°,AB=BC
∵ EC=50m,EB=30m
∴ S正方形ABCD=(40 )2=1600(m2)
∴
∴
在一块正方形的花坛上,欲修建两条直的小路使得两条直的小路将花坛平均分成面积相等的四部分(不考虑道路的宽度).你有几种方法?
设计花坛
我理解了……
我学会了……
……
我知道了……
平行四边形
矩形
菱形
正
方
形
平行四边形、矩形、菱形、正方形的包含关系
想一想
1.已知:正方形ABCD中,点E、F、G 、H分别是AB 、BC 、CD 、DA的中点,试判断四边形EFGH是正方形吗 为什么
A
B
C
D
E
F
G
H
