12.2.2全等三角形判定 边角边 课件(共20张PPT)
文档属性
| 名称 | 12.2.2全等三角形判定 边角边 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 00:00:00 | ||
图片预览



文档简介
(共22张PPT)
人教版
八年级上
全等三角形的判定
第二课时
边角边
某公司接到一批三角形架的加工任务,客户要求是所有的三角形必须全等。为了使产品顺利过关,客户提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等。质检员小王提出了质疑:逐一检查三条边、三个角这6个数据固然可以,但为了提高效率,是不是可以少量一些数据呢?
导入
情景导入
判断三角形全等是否必需3条边、3个角分别相等?相等的条件是否可以少一点?
数学来源于生活
联系所学知识,将小王的质疑转化为数学问题即为
情景导入
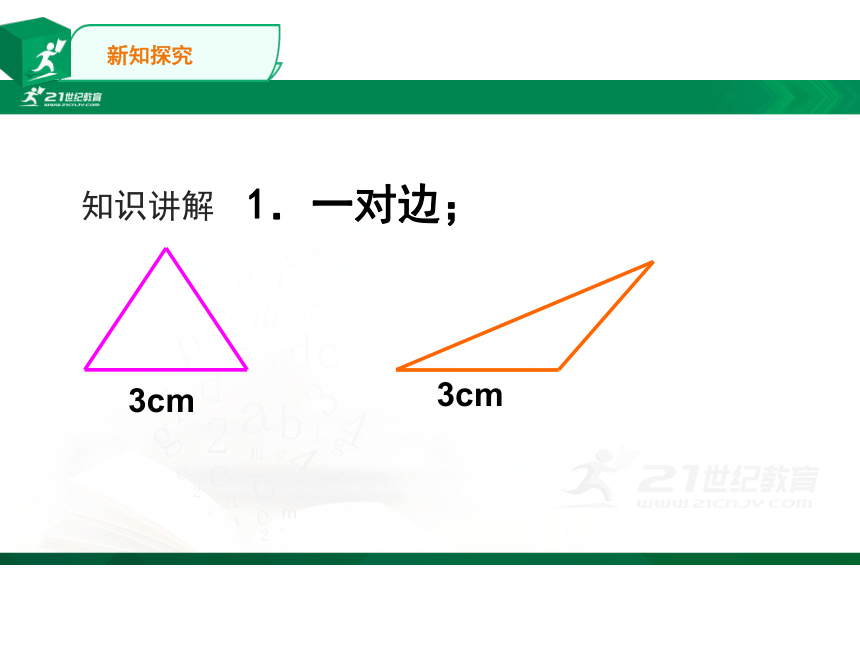
1.一对边;
3cm
3cm
知识讲解
新知探究
活动一:有一对相等条件
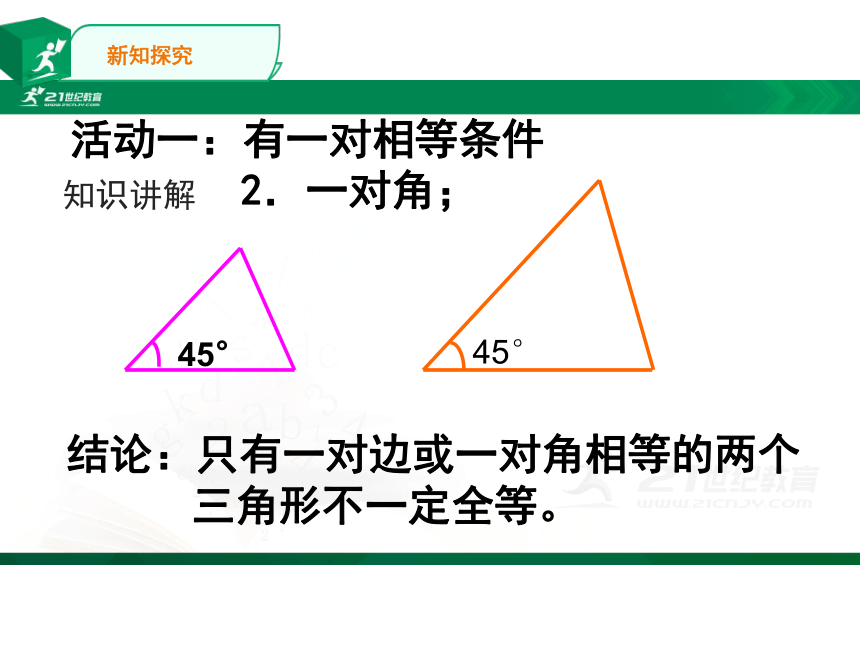
2.一对角;
结论:只有一对边或一对角相等的两个
三角形不一定全等。
45°
45°
知识讲解
新知探究
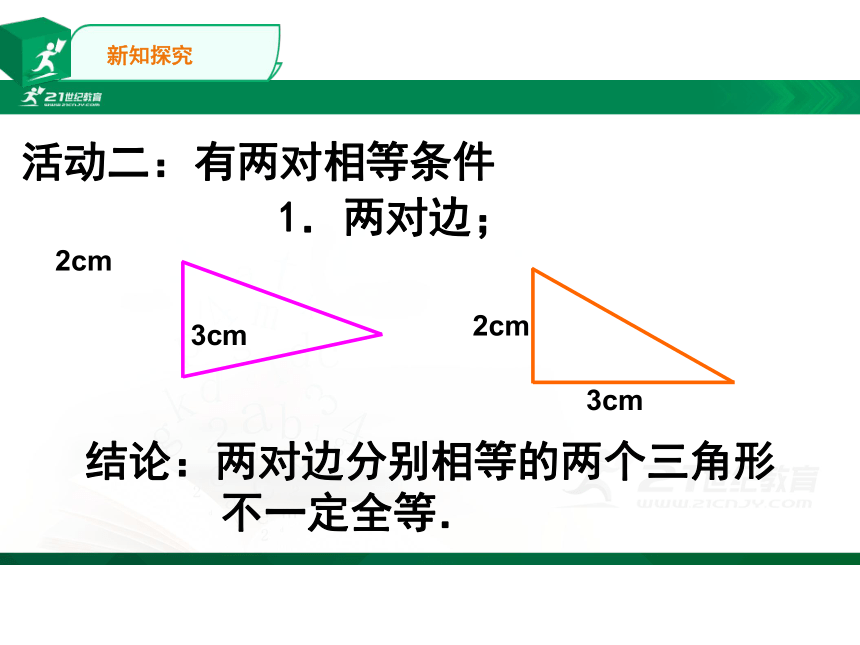
1.两对边;
结论:两对边分别相等的两个三角形
不一定全等.
活动二:有两对相等条件
2cm
3cm
2cm
3cm
新知探究
活动二:有两对相等条件
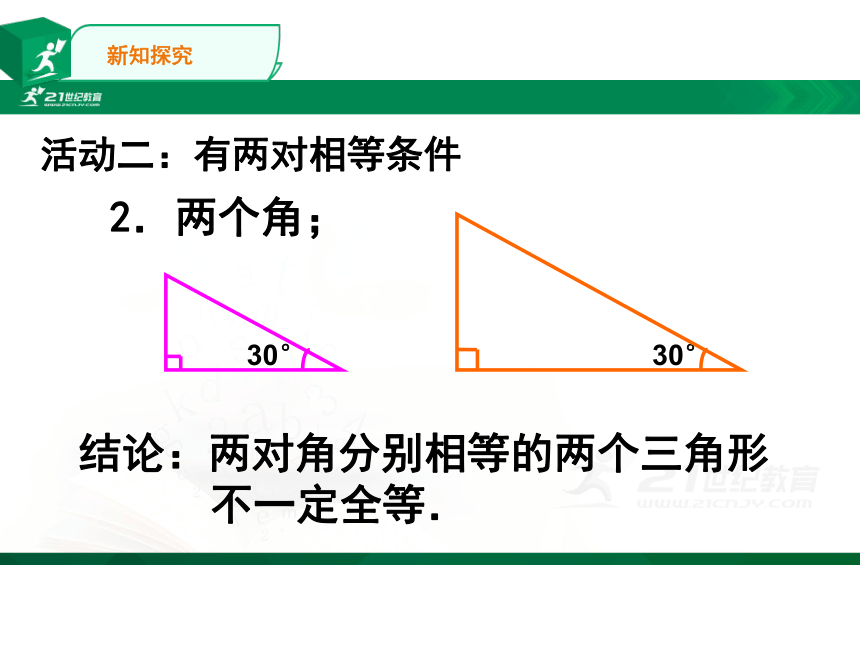
2.两个角;
结论:两对角分别相等的两个三角形
不一定全等.
30°
30°
新知探究
3.一对角一对边;
(1)
一对角和角的一对邻边;
结论:一对角和角的邻边一对邻边相等
的两个三角形不一定全等.
活动二:有两对相等条件
3cm
30°
3cm
30°
新知探究
活动二:有两对相等条件
3.一角一边;
(2)
一对角和对边;
结论:一对角和其对边分别相等的两
个三角形不一定全等.
45°
3cm
45°
3cm
新知探究
一对相等条件
一对边
×
一对角
×
?
两对相等条件
两对边
×
两对角
×
一对边一对角
一角及其邻边
×
一角及其对边
×
?
三对相等条件
两对边一对角
两边及其夹角
两边及其中一边邻角
……
……
?
?
?
?
探索三角形全等的条件
新知探究
用一张长方形纸剪一个直角三角形(只用直尺和剪刀),若要使几位同学剪下的直角三角形都全等,该如何剪呢?
活动三:做一做
新知探究
观察下图中的三角形,猜一猜,哪两个三角形是全等三角形,它们满足了几对相等的条件呢,分别是什么呢?
活动三:观察、猜想
(1)
(2)
(3)
新知探究
活动三:按条件画三角形:
1、画∠MAN=50O;
2、在AM上截取AB=8cm,
在AN上截取AC=6cm;
3、连接BC.
剪下所得的△ABC,与同学所画的比较一下,它们全等吗?
B
C
50°
A
M
N
结论:两边及其夹角分别相等的两个三角形
全等,简写成“边角边”或“SAS”。
新知探究
文字语言
两边和它们的夹角分别相等的两个三角形全等
图形语言
\\
\
A
B
C
\\
\
D
E
F
符号语言
?
归纳整理
数学应用于生活
联系今天所学知识,解决小王的质疑用
数学方法即为
测量这批三角形架对应的
两条边长及它们的夹角相等,就能满足
客户的要求。
归纳整理
例1、如图,AB=AD,∠BAC=∠DAC,
求证:△ABC≌△ADC
D
A
B
C
?
(已知)
(已知)
(公共边)
(SAS)
例题精讲
平移
回归课本
D
A
B
C
例2、如图,AB=AD,∠BAC=∠DAC,
求证:△ABC≌△ADC
(B)
翻折
将△ABC沿AC所在的直线翻折,因为∠BAC=∠DAC,
所以AB落在射线AD上,因为AB=AD,所以点B与点D重合,根据“两点确定一条直线”,可知BC与DC重合,于是△ABC与△ADC重合,即△ABC≌△ADC
.
例题精讲
例3、如图,AB=AC,点D、E分别在AB、AC上,
且AD=AE.
求证:△ABE≌△ACD.
E
A
B
C
D
证明:在△ABE和△ACD中,
∴△ABE≌△ACD
(已知)
(公共角)
(已知)
(SAS)
例题精讲
1、数学来源于生活,又应用于生活,会寻找身边的数学;
2、探索问题的过程中要学会将复杂的条件分类讨论,从简单到复杂;
3、遇到问题要动手操作、验证;
4、会动态地看三角形的全等.
思考:有两边和其中一边的对角分别相等的两个三角形是否全等?
课堂小结
https://www.21cnjy.com/help/help_extract.php
人教版
八年级上
全等三角形的判定
第二课时
边角边
某公司接到一批三角形架的加工任务,客户要求是所有的三角形必须全等。为了使产品顺利过关,客户提出了明确的要求:要逐一检查三角形的三条边、三个角是不是都相等。质检员小王提出了质疑:逐一检查三条边、三个角这6个数据固然可以,但为了提高效率,是不是可以少量一些数据呢?
导入
情景导入
判断三角形全等是否必需3条边、3个角分别相等?相等的条件是否可以少一点?
数学来源于生活
联系所学知识,将小王的质疑转化为数学问题即为
情景导入
1.一对边;
3cm
3cm
知识讲解
新知探究
活动一:有一对相等条件
2.一对角;
结论:只有一对边或一对角相等的两个
三角形不一定全等。
45°
45°
知识讲解
新知探究
1.两对边;
结论:两对边分别相等的两个三角形
不一定全等.
活动二:有两对相等条件
2cm
3cm
2cm
3cm
新知探究
活动二:有两对相等条件
2.两个角;
结论:两对角分别相等的两个三角形
不一定全等.
30°
30°
新知探究
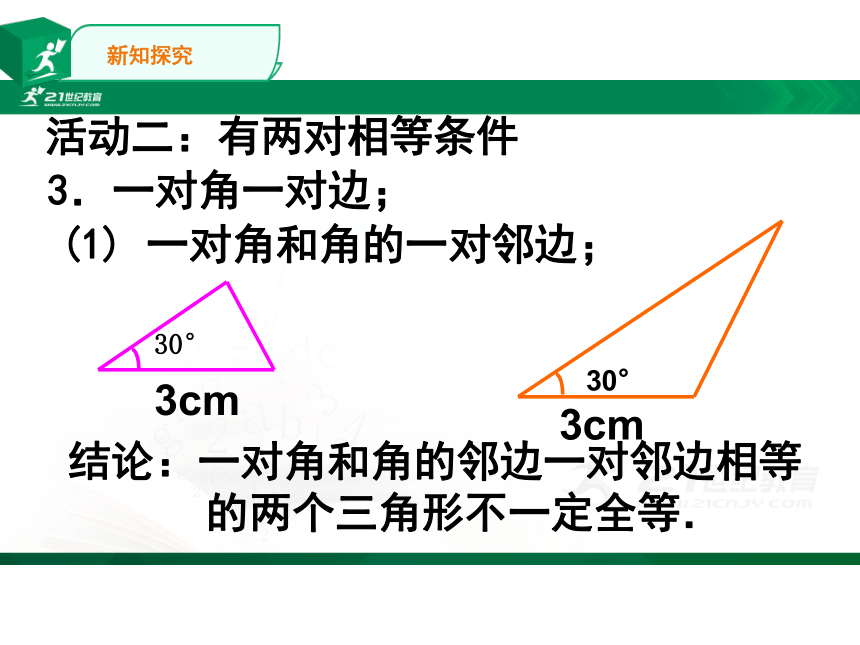
3.一对角一对边;
(1)
一对角和角的一对邻边;
结论:一对角和角的邻边一对邻边相等
的两个三角形不一定全等.
活动二:有两对相等条件
3cm
30°
3cm
30°
新知探究
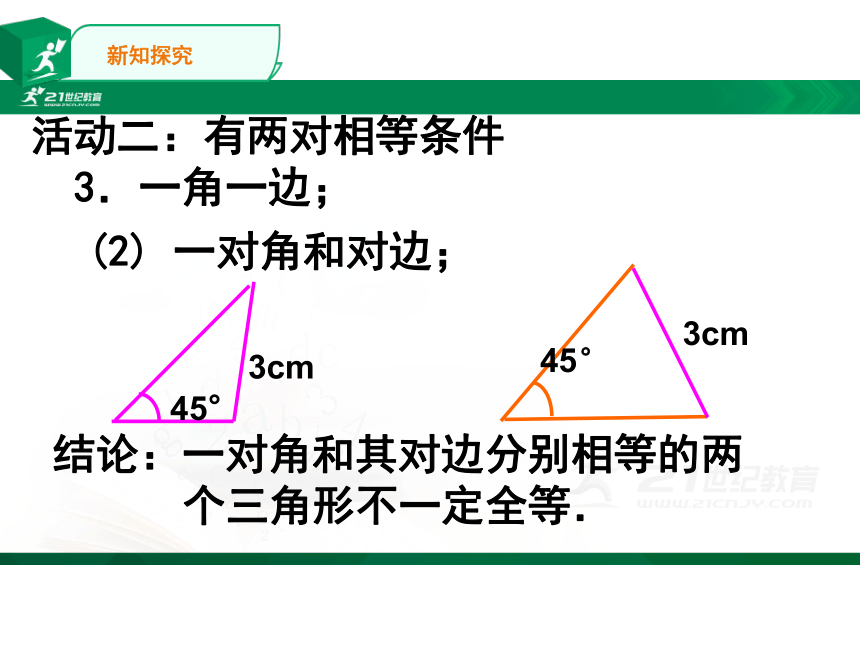
活动二:有两对相等条件
3.一角一边;
(2)
一对角和对边;
结论:一对角和其对边分别相等的两
个三角形不一定全等.
45°
3cm
45°
3cm
新知探究
一对相等条件
一对边
×
一对角
×
?
两对相等条件
两对边
×
两对角
×
一对边一对角
一角及其邻边
×
一角及其对边
×
?
三对相等条件
两对边一对角
两边及其夹角
两边及其中一边邻角
……
……
?
?
?
?
探索三角形全等的条件
新知探究
用一张长方形纸剪一个直角三角形(只用直尺和剪刀),若要使几位同学剪下的直角三角形都全等,该如何剪呢?
活动三:做一做
新知探究
观察下图中的三角形,猜一猜,哪两个三角形是全等三角形,它们满足了几对相等的条件呢,分别是什么呢?
活动三:观察、猜想
(1)
(2)
(3)
新知探究
活动三:按条件画三角形:
1、画∠MAN=50O;
2、在AM上截取AB=8cm,
在AN上截取AC=6cm;
3、连接BC.
剪下所得的△ABC,与同学所画的比较一下,它们全等吗?
B
C
50°
A
M
N
结论:两边及其夹角分别相等的两个三角形
全等,简写成“边角边”或“SAS”。
新知探究
文字语言
两边和它们的夹角分别相等的两个三角形全等
图形语言
\\
\
A
B
C
\\
\
D
E
F
符号语言
?
归纳整理
数学应用于生活
联系今天所学知识,解决小王的质疑用
数学方法即为
测量这批三角形架对应的
两条边长及它们的夹角相等,就能满足
客户的要求。
归纳整理
例1、如图,AB=AD,∠BAC=∠DAC,
求证:△ABC≌△ADC
D
A
B
C
?
(已知)
(已知)
(公共边)
(SAS)
例题精讲
平移
回归课本
D
A
B
C
例2、如图,AB=AD,∠BAC=∠DAC,
求证:△ABC≌△ADC
(B)
翻折
将△ABC沿AC所在的直线翻折,因为∠BAC=∠DAC,
所以AB落在射线AD上,因为AB=AD,所以点B与点D重合,根据“两点确定一条直线”,可知BC与DC重合,于是△ABC与△ADC重合,即△ABC≌△ADC
.
例题精讲
例3、如图,AB=AC,点D、E分别在AB、AC上,
且AD=AE.
求证:△ABE≌△ACD.
E
A
B
C
D
证明:在△ABE和△ACD中,
∴△ABE≌△ACD
(已知)
(公共角)
(已知)
(SAS)
例题精讲
1、数学来源于生活,又应用于生活,会寻找身边的数学;
2、探索问题的过程中要学会将复杂的条件分类讨论,从简单到复杂;
3、遇到问题要动手操作、验证;
4、会动态地看三角形的全等.
思考:有两边和其中一边的对角分别相等的两个三角形是否全等?
课堂小结
https://www.21cnjy.com/help/help_extract.php
