华东师大版数学九年级上册23.3相似三角形 专题复习课件 (共18张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册23.3相似三角形 专题复习课件 (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 778.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 20:34:41 | ||
图片预览





文档简介
(共18张PPT)
23.3相似三角形
专题复习
4、根据相似三角形的传递性,即:
活动一、知识梳理:
相似三角形的判定方法:
1、用定义。
2、用预备定理:根据平行得相似。
3、用判定定理:
(1)两组对应角相等的两个三角形相似。
(2)三组对应边成比例的两个三角形相似。
(3)两组对应边成比例且它们的夹角相等的
两个三角形相似。
活动一、知识梳理:
相似三角形的性质:
1、相似三角形的对应角相等,对应边成比例。
2、相似三角形的对应周长的比、对应高的比、
对应中线的比、对应角平分线的比都等于相似比。
3、相似三角形面积的比等于相似比的平方。
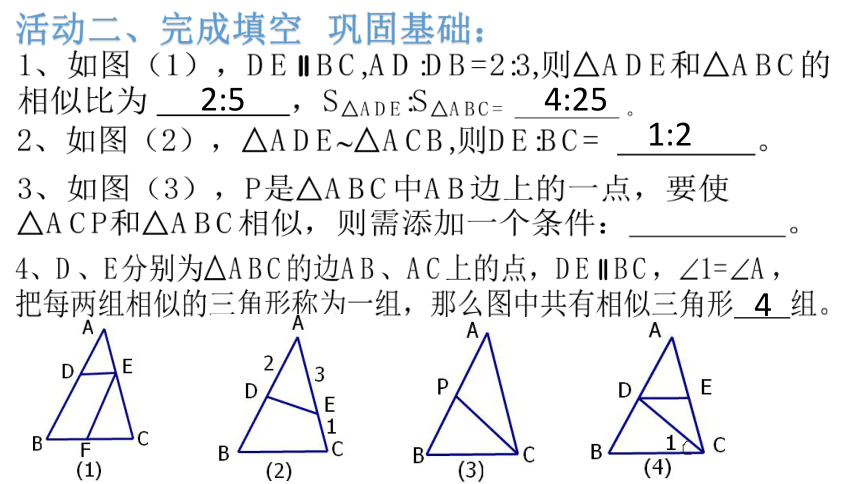
活动二、完成填空
巩固基础:
2:5
4:25
1:2
4
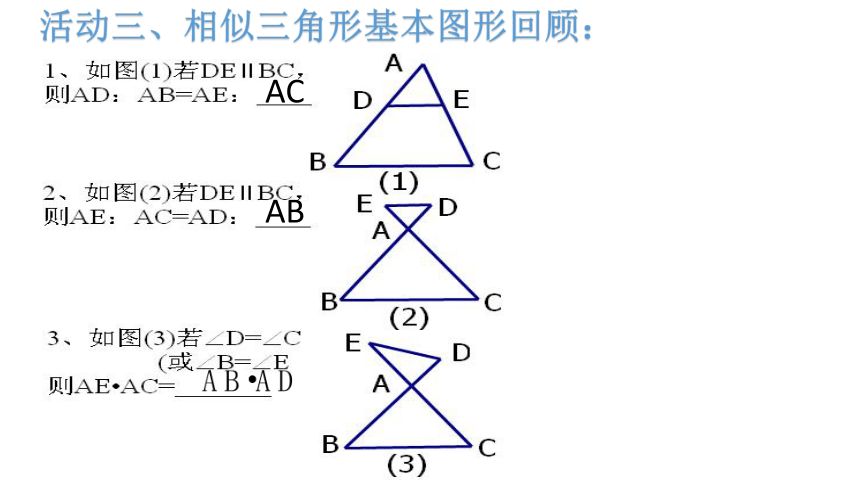
活动三、相似三角形基本图形回顾:
AC
AB
活动三、相似三角形基本图形回顾:
类型
点拨 还可以过C作CH⊥OB于H,根据勾股定理及三角形的面积公式即可求解;
1、 (2019·福州质检)已知:如图(1)所示,在平面直
角坐标系xOy中,∠C=90°,OB=25,OC=20,
若点M是边OC上的一个动点(与点O、C不重合),
过点M作MN∥OB交BC于点N.
则点C的坐标为
(
)
解
点拨
活动四、重点突破:
图(1)
16,-12
解 如图1,过C作CH⊥OB于H,
∵∠OCB=90°,OB=25,OC=20,
∴点C的坐标为(16,-12).
(图1)
2、 如图(2),BD是
O的直径,A,C是
O上的两点,AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.
图(2)
活动四、重点突破:
解
点拨
例3
活动五、难点解析:
∴B(0,2),
解
点拨
(2)M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,
求点M的坐标;
点拨 由M点坐标可表示P、N的坐标,从而可表示出AM、PM、PN、BP的长,分∠BNP=90°和∠NBP=90°两种情况,分别利用相似三角形的性质可得到关于m的方程,求解即可;
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°.
当∠BNP=90°时,有BN⊥MN,
∴BN=OM=m,
活动六、小结:
2、相似三角形由于对应边、对应角的不确定,或者是图形的不确定,常常需要进行分类讨论,解题时根据对应角或对应边来分类.
1、解决计算线段的数量关系,求线段的长度和图形的面积大小等一些问题,先根据已知条件构造相似三角形,再利用相似三角形性质求解。
23.3相似三角形
专题复习
4、根据相似三角形的传递性,即:
活动一、知识梳理:
相似三角形的判定方法:
1、用定义。
2、用预备定理:根据平行得相似。
3、用判定定理:
(1)两组对应角相等的两个三角形相似。
(2)三组对应边成比例的两个三角形相似。
(3)两组对应边成比例且它们的夹角相等的
两个三角形相似。
活动一、知识梳理:
相似三角形的性质:
1、相似三角形的对应角相等,对应边成比例。
2、相似三角形的对应周长的比、对应高的比、
对应中线的比、对应角平分线的比都等于相似比。
3、相似三角形面积的比等于相似比的平方。
活动二、完成填空
巩固基础:
2:5
4:25
1:2
4
活动三、相似三角形基本图形回顾:
AC
AB
活动三、相似三角形基本图形回顾:
类型
点拨 还可以过C作CH⊥OB于H,根据勾股定理及三角形的面积公式即可求解;
1、 (2019·福州质检)已知:如图(1)所示,在平面直
角坐标系xOy中,∠C=90°,OB=25,OC=20,
若点M是边OC上的一个动点(与点O、C不重合),
过点M作MN∥OB交BC于点N.
则点C的坐标为
(
)
解
点拨
活动四、重点突破:
图(1)
16,-12
解 如图1,过C作CH⊥OB于H,
∵∠OCB=90°,OB=25,OC=20,
∴点C的坐标为(16,-12).
(图1)
2、 如图(2),BD是
O的直径,A,C是
O上的两点,AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长.
图(2)
活动四、重点突破:
解
点拨
例3
活动五、难点解析:
∴B(0,2),
解
点拨
(2)M(m,0)为线段OA上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,
求点M的坐标;
点拨 由M点坐标可表示P、N的坐标,从而可表示出AM、PM、PN、BP的长,分∠BNP=90°和∠NBP=90°两种情况,分别利用相似三角形的性质可得到关于m的方程,求解即可;
∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,
∵△BPN和△APM相似,且∠BPN=∠APM,
∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°.
当∠BNP=90°时,有BN⊥MN,
∴BN=OM=m,
活动六、小结:
2、相似三角形由于对应边、对应角的不确定,或者是图形的不确定,常常需要进行分类讨论,解题时根据对应角或对应边来分类.
1、解决计算线段的数量关系,求线段的长度和图形的面积大小等一些问题,先根据已知条件构造相似三角形,再利用相似三角形性质求解。
