2.1.1 认识无理数 课件(共20张PPT)
文档属性
| 名称 | 2.1.1 认识无理数 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 23:06:49 | ||
图片预览








文档简介
(共20张PPT)
导入新课
小红是刚升入八年级的新生,一个周末的上午,当工程师的爸爸给小红出了一道数学题:一个边长为6cm的正方形木板,按如图的痕迹锯掉四个一样的直角三角形.请计算剩下的正方形木板的面积是多少?剩下的正方形木板的边长又是多少厘米呢?见过这个数吗?你能帮小红解决这个问题吗?
2
2.1
认识无理数
学习目标
1.了解无理数的基本概念.(重点)
2.借助计算器估计无理数的近似值.
新知讲解
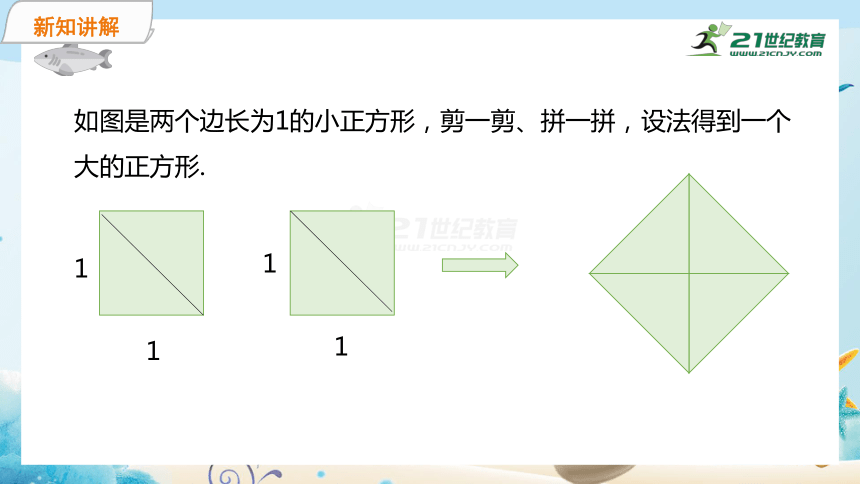
如图是两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
1
1
1
1
新知讲解
(1)设大正方形的边长为a,a满足什么条件?
因为拼成的大正方形的面积是2,如果大正方形的边长为a,a应该满足a2=2.
新知讲解
(2)a可能是整数吗?说说你的理由.
(3)a可能是分数吗?说说你的理由.
没有两个相等的整数的积等于2,也没有两个相等的分数的积等于2,
因此a不可能是有理数.
事实上,我们可以证明,在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数.
新知讲解
【做一做】
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
由勾股定理可知,直角三角形的斜边的平方为5,所以正方形的面积是5.
新知讲解
【做一做】
(2)设该正方形的边长为b,b满足什么条件?
b2
=
5
新知讲解
【做一做】
(3)b是有理数吗?
没有一个整数或分数的平方为5,也就是没有一个有理数的平方为5,所以b不是有理数.
新知讲解
【总结提升】
在上面的两个问题中,数a,b确实存在,但都不是有理数.
在解决实际问题时,我们发现原来学习的有理数远远不能满足解决实际问题的需要,也就是存在这样的一类数,既不是整数也不是分数,或者说不是有理数.
例
下列各数中,哪些是有理数?哪些是无理数?
3.14,-
,0.57,0.1010001000001…(相邻两个1之间0的个数逐次加2).
.
.
解:有理数有:3.14,
,
0.57;
.
.
无理数有:0.1010001000001….
典例解析
整数有____________________________
有理数有_________________________
无理数有__________________________
填空:在实数
【跟踪训练】
1.圆周率
及一些最终结果含有
的数.
2.有一定的规律,但不循环的无限小数.
无理数的特征:
1.下列各数:
1,
(相邻两个3之间0的个数逐次加1)中,无理数的个数是(
)
A.2个
B.3个
C.4个
D.5个
【解析】无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)是无理数,其他是有理数.
A
当堂练习
【解析】因为3.14是小数,
是分数,
是无限循环小
数,所以选项A,B,D都是有理数;
是无限不循环小数,所以是无理数.
2.下列各数中,是无理数的为(
)
A.
3.14
B.
C.
D.
C
?
?
?
?
?
(1)有限小数是有理数;
(
)
(2)无限小数都是无理数;
(
)
(3)无理数都是无限小数;
(
)
(4)有理数是有限小数.
(
)
3.
判断题
╳
√
√
╳
4.以下各正方形的边长是无理数的是(
)
A.面积为25的正方形;
B.面积为
的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
课堂总结
认识无理数
无理数的概念及认识
借助计算器求无理数的近似值
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
导入新课
小红是刚升入八年级的新生,一个周末的上午,当工程师的爸爸给小红出了一道数学题:一个边长为6cm的正方形木板,按如图的痕迹锯掉四个一样的直角三角形.请计算剩下的正方形木板的面积是多少?剩下的正方形木板的边长又是多少厘米呢?见过这个数吗?你能帮小红解决这个问题吗?
2
2.1
认识无理数
学习目标
1.了解无理数的基本概念.(重点)
2.借助计算器估计无理数的近似值.
新知讲解
如图是两个边长为1的小正方形,剪一剪、拼一拼,设法得到一个大的正方形.
1
1
1
1
新知讲解
(1)设大正方形的边长为a,a满足什么条件?
因为拼成的大正方形的面积是2,如果大正方形的边长为a,a应该满足a2=2.
新知讲解
(2)a可能是整数吗?说说你的理由.
(3)a可能是分数吗?说说你的理由.
没有两个相等的整数的积等于2,也没有两个相等的分数的积等于2,
因此a不可能是有理数.
事实上,我们可以证明,在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数.
新知讲解
【做一做】
(1)如图,以直角三角形的斜边为边的正方形的面积是多少?
由勾股定理可知,直角三角形的斜边的平方为5,所以正方形的面积是5.
新知讲解
【做一做】
(2)设该正方形的边长为b,b满足什么条件?
b2
=
5
新知讲解
【做一做】
(3)b是有理数吗?
没有一个整数或分数的平方为5,也就是没有一个有理数的平方为5,所以b不是有理数.
新知讲解
【总结提升】
在上面的两个问题中,数a,b确实存在,但都不是有理数.
在解决实际问题时,我们发现原来学习的有理数远远不能满足解决实际问题的需要,也就是存在这样的一类数,既不是整数也不是分数,或者说不是有理数.
例
下列各数中,哪些是有理数?哪些是无理数?
3.14,-
,0.57,0.1010001000001…(相邻两个1之间0的个数逐次加2).
.
.
解:有理数有:3.14,
,
0.57;
.
.
无理数有:0.1010001000001….
典例解析
整数有____________________________
有理数有_________________________
无理数有__________________________
填空:在实数
【跟踪训练】
1.圆周率
及一些最终结果含有
的数.
2.有一定的规律,但不循环的无限小数.
无理数的特征:
1.下列各数:
1,
(相邻两个3之间0的个数逐次加1)中,无理数的个数是(
)
A.2个
B.3个
C.4个
D.5个
【解析】无限不循环小数是无理数,其中
(相邻两个3之间0的个数逐次加1)是无理数,其他是有理数.
A
当堂练习
【解析】因为3.14是小数,
是分数,
是无限循环小
数,所以选项A,B,D都是有理数;
是无限不循环小数,所以是无理数.
2.下列各数中,是无理数的为(
)
A.
3.14
B.
C.
D.
C
?
?
?
?
?
(1)有限小数是有理数;
(
)
(2)无限小数都是无理数;
(
)
(3)无理数都是无限小数;
(
)
(4)有理数是有限小数.
(
)
3.
判断题
╳
√
√
╳
4.以下各正方形的边长是无理数的是(
)
A.面积为25的正方形;
B.面积为
的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
C
课堂总结
认识无理数
无理数的概念及认识
借助计算器求无理数的近似值
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
