湖北省安陆市第一高级中学人教A版选修2-2课本例题习题改编
文档属性
| 名称 | 湖北省安陆市第一高级中学人教A版选修2-2课本例题习题改编 |
|
|
| 格式 | zip | ||
| 文件大小 | 244.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-18 00:00:00 | ||
图片预览



文档简介
人教A版选修2-2课本例题习题改编
1.原题(选修2-2第十一页习题1.1B组第一题)改编 在高台跳水中,t s时运动员相对水面的高度(单位:m)是则t=2 s时的速度是_______.
解: HYPERLINK "http://www." 由导数的概念知:t=2 s时的速度为
2.原题(选修2-2第十九页习题1.2B组第一题)改编记 HYPERLINK "http://www." ,则A,B,C的大小关系是( )
A. B. HYPERLINK "http://www."
C. ( http: / / www. ) D.
解: HYPERLINK "http://www." 记
根据导数的几何意义A表示sinx在点M处的切线的斜率,B表示sinx在点N处的切线的斜率,C表示直线MN的斜率, 根据正弦的图像可知A>C>B故选B
( http: / / www. )
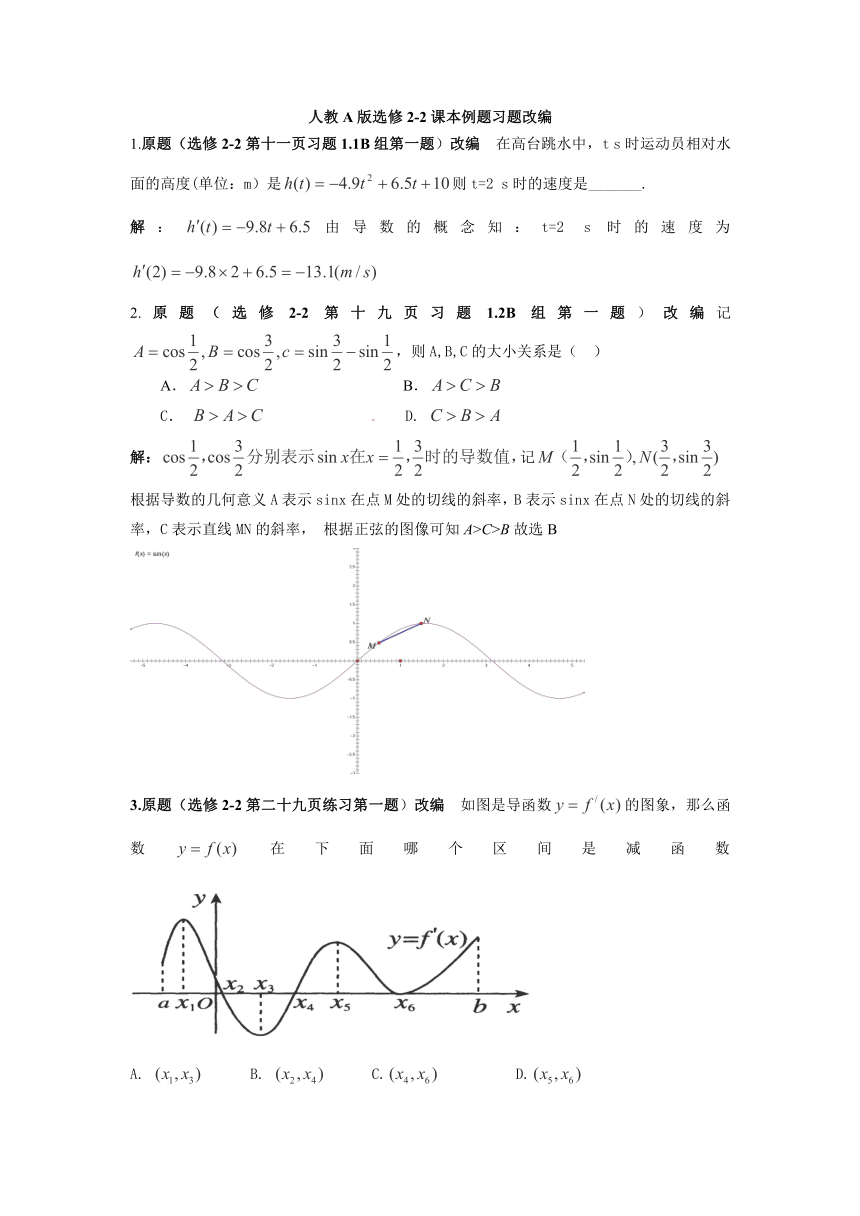
3.原题(选修2-2第二十九页练习第一题)改编 如图是导函数的图象,那么函数 HYPERLINK "http://www." 在下面哪个区间是减函数
A. HYPERLINK "http://www." B. C. HYPERLINK "http://www." D.
解:函数的单调递减区间就是其导函数小于零的区间,故选B
4.原题(选修2-2第三十二页习题1.3B组第1题(4))改编 设 HYPERLINK "http://www." ,记 HYPERLINK "http://www." 试比较a,b,c的大小关系为( )
A HYPERLINK "http://www." B C HYPERLINK "http://www." D
解:先证明不等式 HYPERLINK "http://www." x>0
设
因为 HYPERLINK "http://www." EMBED Equation.DSMT4 所以,当 HYPERLINK "http://www." 时, HYPERLINK "http://www." 单调递增,;当 HYPERLINK "http://www." 时 ( http: / / www. )单调递减, HYPERLINK "http://www." ;当x=1时,显然,因此 HYPERLINK "http://www."
设
HYPERLINK "http://www." 当 HYPERLINK "http://www." HYPERLINK "http://www."
即
综上:有 HYPERLINK "http://www." ,x>0成立
HYPERLINK "http://www." HYPERLINK "http://www." HYPERLINK "http://www." 故选A
5.原题(选修2-2第三十七页习题1.4A组第1题)改编 用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是_________.
解:设长方体的宽为xm,则长为2xm,高 HYPERLINK "http://www." .
故长方体的体积为
从而 HYPERLINK "http://www."
令,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时, HYPERLINK "http://www." >0;当1<x<时, HYPERLINK "http://www." <0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值.
从而最大体积V=3(m3 ( http: / / www. )),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3.
6.原题(选修2-2第四十五页练习第二题)改编 一辆汽车在笔直的公路上变速行驶,设汽车在时刻t的速度为v(t)=-t2+4,(t)(t的单位:h, v的单位:km/h)则这辆车行驶的最大位移是______km
解:当汽车行驶位移最大时,v(t)=0.又v(t)=-t2+4=0且 HYPERLINK "http://www." ,则t=2
,故填 HYPERLINK "http://www."
7.原题(选修2-2第五十页习题1.5A组第四题)改编 ________
解: HYPERLINK "http://www." ,而表 ( http: / / www. )示单位圆x2+y2=1在第一象限内的部分面积, HYPERLINK "http://www."
HYPERLINK "http://www." 2(e-1-)= HYPERLINK "http://www." 故填.
8.原题(选修2-2第五十三页 ( http: / / www. )例2)改编 曲线与直线y= HYPERLINK "http://www." 围成的封闭图形的面积为( )A. B. HYPERLINK "http://www." C. D. HYPERLINK "http://www."
解:由与 HYPERLINK "http://www." 得,所以曲线 HYPERLINK "http://www." 与直线y=围成的封闭图形的面积 HYPERLINK "http://www." = 故选D
9.原题(选修2-2第五十六页例1)改编 由曲线 HYPERLINK "http://www." ,所围成图形的面积为____________
解:联立 HYPERLINK "http://www." 得焦点坐标(0,0),(1,1)
∴
HYPERLINK "http://www."
而 HYPERLINK "http://www." EMBED Equation.3 表示单位圆 HYPERLINK "http://www." EMBED Equation.DSMT4 在第一象限内的部分
∴ HYPERLINK "http://www." = ∴ HYPERLINK "http://www." 故填
( http: / / www. )
10.原题(选修2-2第七十八页练习3)改编 设P是内一点, HYPERLINK "http://www." 三边上的高分别为、 HYPERLINK "http://www." 、,P到三边的距离依次为 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,则有______________; ( http: / / www. )类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是、 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,P到这四个面的距离依次是、 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,则有_________________。
解:用等面积法可得, 所以
HYPERLINK "http://www." EMBED Equation.3 ,类比到空间有 HYPERLINK "http://www."
11.原题(选修2-2第八十二页阅读与思考)改编 如图,点 HYPERLINK "http://www." 为斜三棱柱的侧棱 HYPERLINK "http://www." 上一点,交 HYPERLINK "http://www." 于点, HYPERLINK "http://www." 交于点 HYPERLINK "http://www." .
(1)求证: HYPERLINK "http://www." ;
(2) 在任意中有余弦定理:
HYPERLINK "http://www." .
拓展到空间,类比三角形的余弦定理,
写出斜三棱柱的三个侧面面积与其中
两个侧面所成的二面角之间的关系式,并予以证明.
解:(1) 证明:;
(2) 在斜三棱柱 HYPERLINK "http://www." 中,有,其中 HYPERLINK "http://www." 为平面与平面 HYPERLINK "http://www." 所成的二面角.
HYPERLINK "http://www." 上述的二面角为,在 HYPERLINK "http://www." 中, HYPERLINK "http://www." ,
由于 ( http: / / www. )
∴有.
12.原题(选修2-2第九十六页习题2.3A组第一题)改编 在数列 HYPERLINK "http://www." 中,,则数列 HYPERLINK "http://www." 的通项公式为____________
解:本题有多种求法,“归纳——猜想——证明”是其中之一 HYPERLINK "http://www." 猜想
下面用数学归纳法证明:(1)当n=1时, HYPERLINK "http://www." ,猜想成立
(2)假设当n=k时猜想成立,则
当n=k+1时猜想也成立,综合(1)(2),对 HYPERLINK "http://www." 猜想都成立.故应填
13.原题(选修2-2第页习题 ( http: / / www. )一百一十二页习题3.2A组第4题(4))改编 复数 HYPERLINK "http://www." ( )
A. B. HYPERLINK "http://www." C. D. HYPERLINK "http://www."
解:
HYPERLINK "http://www."
其共轭复数为 HYPERLINK "http://www." ,故选B
1.原题(选修2-2第十一页习题1.1B组第一题)改编 在高台跳水中,t s时运动员相对水面的高度(单位:m)是则t=2 s时的速度是_______.
解: HYPERLINK "http://www." 由导数的概念知:t=2 s时的速度为
2.原题(选修2-2第十九页习题1.2B组第一题)改编记 HYPERLINK "http://www." ,则A,B,C的大小关系是( )
A. B. HYPERLINK "http://www."
C. ( http: / / www. ) D.
解: HYPERLINK "http://www." 记
根据导数的几何意义A表示sinx在点M处的切线的斜率,B表示sinx在点N处的切线的斜率,C表示直线MN的斜率, 根据正弦的图像可知A>C>B故选B
( http: / / www. )
3.原题(选修2-2第二十九页练习第一题)改编 如图是导函数的图象,那么函数 HYPERLINK "http://www." 在下面哪个区间是减函数
A. HYPERLINK "http://www." B. C. HYPERLINK "http://www." D.
解:函数的单调递减区间就是其导函数小于零的区间,故选B
4.原题(选修2-2第三十二页习题1.3B组第1题(4))改编 设 HYPERLINK "http://www." ,记 HYPERLINK "http://www." 试比较a,b,c的大小关系为( )
A HYPERLINK "http://www." B C HYPERLINK "http://www." D
解:先证明不等式 HYPERLINK "http://www." x>0
设
因为 HYPERLINK "http://www." EMBED Equation.DSMT4 所以,当 HYPERLINK "http://www." 时, HYPERLINK "http://www." 单调递增,;当 HYPERLINK "http://www." 时 ( http: / / www. )单调递减, HYPERLINK "http://www." ;当x=1时,显然,因此 HYPERLINK "http://www."
设
HYPERLINK "http://www." 当 HYPERLINK "http://www." HYPERLINK "http://www."
即
综上:有 HYPERLINK "http://www." ,x>0成立
HYPERLINK "http://www." HYPERLINK "http://www." HYPERLINK "http://www." 故选A
5.原题(选修2-2第三十七页习题1.4A组第1题)改编 用长为18 m的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是_________.
解:设长方体的宽为xm,则长为2xm,高 HYPERLINK "http://www." .
故长方体的体积为
从而 HYPERLINK "http://www."
令,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时, HYPERLINK "http://www." >0;当1<x<时, HYPERLINK "http://www." <0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值.
从而最大体积V=3(m3 ( http: / / www. )),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3.
6.原题(选修2-2第四十五页练习第二题)改编 一辆汽车在笔直的公路上变速行驶,设汽车在时刻t的速度为v(t)=-t2+4,(t)(t的单位:h, v的单位:km/h)则这辆车行驶的最大位移是______km
解:当汽车行驶位移最大时,v(t)=0.又v(t)=-t2+4=0且 HYPERLINK "http://www." ,则t=2
,故填 HYPERLINK "http://www."
7.原题(选修2-2第五十页习题1.5A组第四题)改编 ________
解: HYPERLINK "http://www." ,而表 ( http: / / www. )示单位圆x2+y2=1在第一象限内的部分面积, HYPERLINK "http://www."
HYPERLINK "http://www." 2(e-1-)= HYPERLINK "http://www." 故填.
8.原题(选修2-2第五十三页 ( http: / / www. )例2)改编 曲线与直线y= HYPERLINK "http://www." 围成的封闭图形的面积为( )A. B. HYPERLINK "http://www." C. D. HYPERLINK "http://www."
解:由与 HYPERLINK "http://www." 得,所以曲线 HYPERLINK "http://www." 与直线y=围成的封闭图形的面积 HYPERLINK "http://www." = 故选D
9.原题(选修2-2第五十六页例1)改编 由曲线 HYPERLINK "http://www." ,所围成图形的面积为____________
解:联立 HYPERLINK "http://www." 得焦点坐标(0,0),(1,1)
∴
HYPERLINK "http://www."
而 HYPERLINK "http://www." EMBED Equation.3 表示单位圆 HYPERLINK "http://www." EMBED Equation.DSMT4 在第一象限内的部分
∴ HYPERLINK "http://www." = ∴ HYPERLINK "http://www." 故填
( http: / / www. )
10.原题(选修2-2第七十八页练习3)改编 设P是内一点, HYPERLINK "http://www." 三边上的高分别为、 HYPERLINK "http://www." 、,P到三边的距离依次为 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,则有______________; ( http: / / www. )类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是、 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,P到这四个面的距离依次是、 HYPERLINK "http://www." 、、 HYPERLINK "http://www." ,则有_________________。
解:用等面积法可得, 所以
HYPERLINK "http://www." EMBED Equation.3 ,类比到空间有 HYPERLINK "http://www."
11.原题(选修2-2第八十二页阅读与思考)改编 如图,点 HYPERLINK "http://www." 为斜三棱柱的侧棱 HYPERLINK "http://www." 上一点,交 HYPERLINK "http://www." 于点, HYPERLINK "http://www." 交于点 HYPERLINK "http://www." .
(1)求证: HYPERLINK "http://www." ;
(2) 在任意中有余弦定理:
HYPERLINK "http://www." .
拓展到空间,类比三角形的余弦定理,
写出斜三棱柱的三个侧面面积与其中
两个侧面所成的二面角之间的关系式,并予以证明.
解:(1) 证明:;
(2) 在斜三棱柱 HYPERLINK "http://www." 中,有,其中 HYPERLINK "http://www." 为平面与平面 HYPERLINK "http://www." 所成的二面角.
HYPERLINK "http://www." 上述的二面角为,在 HYPERLINK "http://www." 中, HYPERLINK "http://www." ,
由于 ( http: / / www. )
∴有.
12.原题(选修2-2第九十六页习题2.3A组第一题)改编 在数列 HYPERLINK "http://www." 中,,则数列 HYPERLINK "http://www." 的通项公式为____________
解:本题有多种求法,“归纳——猜想——证明”是其中之一 HYPERLINK "http://www." 猜想
下面用数学归纳法证明:(1)当n=1时, HYPERLINK "http://www." ,猜想成立
(2)假设当n=k时猜想成立,则
当n=k+1时猜想也成立,综合(1)(2),对 HYPERLINK "http://www." 猜想都成立.故应填
13.原题(选修2-2第页习题 ( http: / / www. )一百一十二页习题3.2A组第4题(4))改编 复数 HYPERLINK "http://www." ( )
A. B. HYPERLINK "http://www." C. D. HYPERLINK "http://www."
解:
HYPERLINK "http://www."
其共轭复数为 HYPERLINK "http://www." ,故选B
