鲁教版(五四制)九上3.4.3二次函数y=ax2+bx+c的图象和性质 教案
文档属性
| 名称 | 鲁教版(五四制)九上3.4.3二次函数y=ax2+bx+c的图象和性质 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 501.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 17:43:15 | ||
图片预览

文档简介
3.4
二次函数函数y=a(x-h)2+k
的图象和性质(3)
内容解析
《义务教育数学课程标本(2011版)》在“学段目标”中提出“体验从具体情境中抽象出数学符号的过程,理解函数;探索具体问题中的数量关系和变化规律,掌握用函数进行表述的方法;通过用函数等表述数量关系的过程,体会模型的思想,建立符号意识”.
二次函数是在学生系统学习了函数概念,基本掌握了函数的性质的基础上进行研究的,学生在前几节课中,已学习过了二次函数的概念和函数y=ax2、函数y=ax2+c、函数y=a(x-h)2的图象和性质,学生在此过程中,已学会用列表、描点的方法作出二次函数的图象,并积累了如何从图象的角度研究函数性质的经验.另外,学生在初二学过图形平移变换的知识,这些知识储备为本节课的学习奠定了良好的基础,使学生具备了掌握本节知识的基本技能.因此,在本节课中,他们可以联系初二已学图形平移变换知识,运用图象变换的观点把二次函数y=ax2的图象经过一定的平移变换,从特殊到一般,得到二次函数y=a(x-h)2+k的图象和性质.
知识关联
教学设计
1、
学习目标
1.理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系.
2.会确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
3.经历函数y=a(x-h)2+k性质的探索过程,理解函数y=a(x-h)2+k的性质.
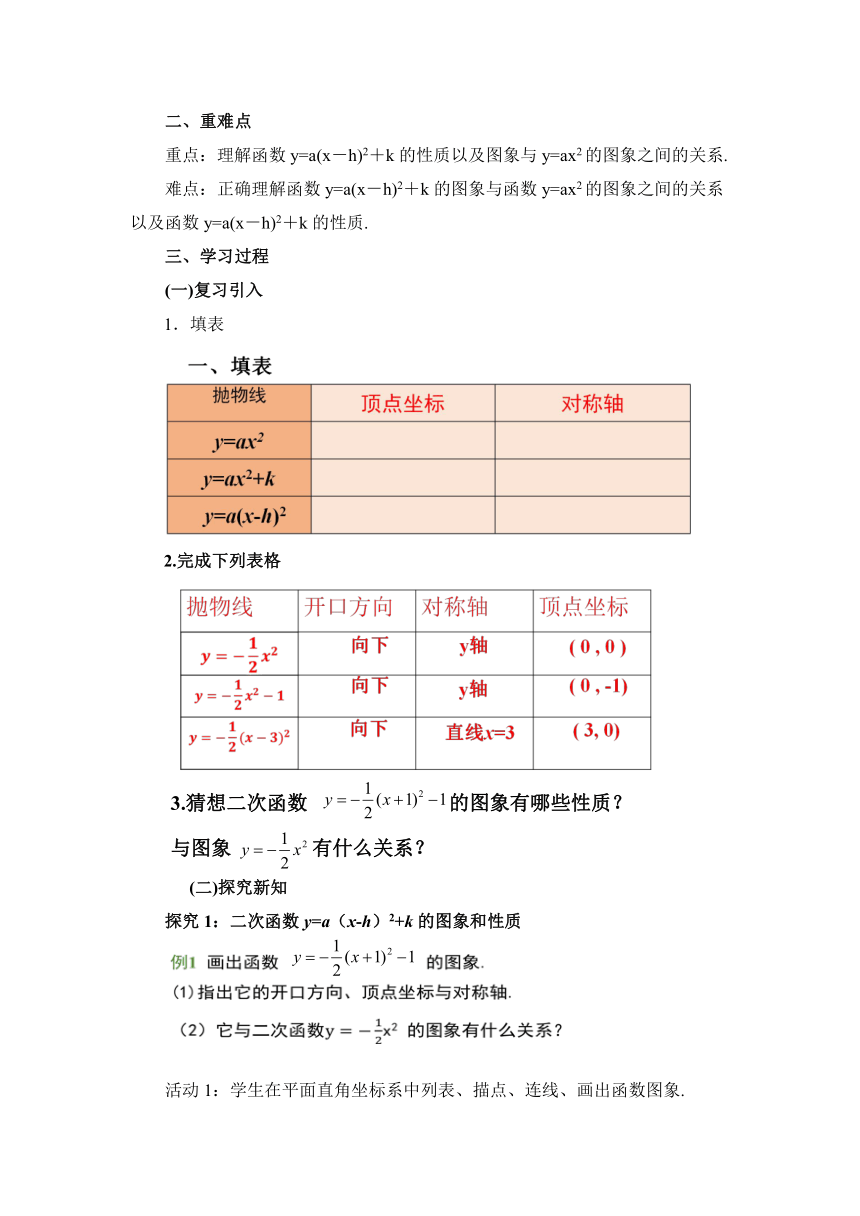
二、重难点
重点:理解函数y=a(x-h)2+k的性质以及图象与y=ax2的图象之间的关系.
难点:正确理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系以及函数y=a(x-h)2+k的性质.
三、学习过程
(一)复习引入
1.填表
2.完成下列表格
3.猜想二次函数
的图象有哪些性质?
与图象
有什么关系?
(二)探究新知
探究1:二次函数y=a(x-h)2+k的图象和性质
活动1:学生在平面直角坐标系中列表、描点、连线、画出函数图象.
(2)根据函数图象说出抛物线的开口方向、对称轴、顶点坐标及增减性.
思考
说出抛物线y=2(x+1)2-2的开口方向、对称轴、顶点坐标
(3)议一议:二次函数y=a(x-h)2+k的图象与y=ax2有什么关系?
学生思考,总结规律,填写表格:
知识要点1:二次函数
y=a(x-h)2+k(a
≠
0)的性质
图象特征二次函数
开口方向
对称轴
顶点坐标
最值
增减性
a>o
ay=a(x-h)2+k
练习1:完成下列表格:
二次函数
开口方向
对称轴
顶点坐标
x取何值时,y随x的增大而增大
y=2(x+3)2+5
y=-3(x-1)2-2
y=4(x-3)2+7
y=-5(2-x)2-6
探究2:二次函数y=a(x-h)2+k与y=ax2的关系
观察函数图象思考:怎样平移抛物线
就可以得到抛物线
?
活动2:小组内交流,观察图象探究出平移方法和规律,学生代表口答.
活动3:目前为止,二次函数图象我们共研究了哪些类型?从解析式来看,它们之间的关系是什么?从图象来看,它们有什么关系?
知识要点2:二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的.
(三)例题点拨
例2.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
(四)达标测试
拓展提高
(五)小结
1.知识方面
(1)二次函数y=a(x-h)2+k的性质:
(a)a的符号决定抛物线的开口方向
(b)对称轴是直线x=h
(c)顶点坐标是(h,k)
(2)抛物线y=a(x-h)2+k与y
=
ax2的关系及平移规律.
2.思想方法方面
用观察、比较、归纳、概括的方法探究二次函数y=a(x-h)2+k的性质;用数形结合思想探究
函数的性质,建立二次函数模型.
(五)作业
课本86页习题3.8第1、2题.
二次函数函数y=a(x-h)2+k
的图象和性质(3)
内容解析
《义务教育数学课程标本(2011版)》在“学段目标”中提出“体验从具体情境中抽象出数学符号的过程,理解函数;探索具体问题中的数量关系和变化规律,掌握用函数进行表述的方法;通过用函数等表述数量关系的过程,体会模型的思想,建立符号意识”.
二次函数是在学生系统学习了函数概念,基本掌握了函数的性质的基础上进行研究的,学生在前几节课中,已学习过了二次函数的概念和函数y=ax2、函数y=ax2+c、函数y=a(x-h)2的图象和性质,学生在此过程中,已学会用列表、描点的方法作出二次函数的图象,并积累了如何从图象的角度研究函数性质的经验.另外,学生在初二学过图形平移变换的知识,这些知识储备为本节课的学习奠定了良好的基础,使学生具备了掌握本节知识的基本技能.因此,在本节课中,他们可以联系初二已学图形平移变换知识,运用图象变换的观点把二次函数y=ax2的图象经过一定的平移变换,从特殊到一般,得到二次函数y=a(x-h)2+k的图象和性质.
知识关联
教学设计
1、
学习目标
1.理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系.
2.会确定函数y=a(x-h)2+k的图象的开口方向、对称轴和顶点坐标.
3.经历函数y=a(x-h)2+k性质的探索过程,理解函数y=a(x-h)2+k的性质.
二、重难点
重点:理解函数y=a(x-h)2+k的性质以及图象与y=ax2的图象之间的关系.
难点:正确理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系以及函数y=a(x-h)2+k的性质.
三、学习过程
(一)复习引入
1.填表
2.完成下列表格
3.猜想二次函数
的图象有哪些性质?
与图象
有什么关系?
(二)探究新知
探究1:二次函数y=a(x-h)2+k的图象和性质
活动1:学生在平面直角坐标系中列表、描点、连线、画出函数图象.
(2)根据函数图象说出抛物线的开口方向、对称轴、顶点坐标及增减性.
思考
说出抛物线y=2(x+1)2-2的开口方向、对称轴、顶点坐标
(3)议一议:二次函数y=a(x-h)2+k的图象与y=ax2有什么关系?
学生思考,总结规律,填写表格:
知识要点1:二次函数
y=a(x-h)2+k(a
≠
0)的性质
图象特征二次函数
开口方向
对称轴
顶点坐标
最值
增减性
a>o
a
练习1:完成下列表格:
二次函数
开口方向
对称轴
顶点坐标
x取何值时,y随x的增大而增大
y=2(x+3)2+5
y=-3(x-1)2-2
y=4(x-3)2+7
y=-5(2-x)2-6
探究2:二次函数y=a(x-h)2+k与y=ax2的关系
观察函数图象思考:怎样平移抛物线
就可以得到抛物线
?
活动2:小组内交流,观察图象探究出平移方法和规律,学生代表口答.
活动3:目前为止,二次函数图象我们共研究了哪些类型?从解析式来看,它们之间的关系是什么?从图象来看,它们有什么关系?
知识要点2:二次函数y=ax2
与y=a(x-h)2+k的关系
可以看作互相平移得到的.
(三)例题点拨
例2.已知二次函数y=a(x-1)2-c的图象如图所示,则一次函数y=ax+c的大致图象可能是( )
(四)达标测试
拓展提高
(五)小结
1.知识方面
(1)二次函数y=a(x-h)2+k的性质:
(a)a的符号决定抛物线的开口方向
(b)对称轴是直线x=h
(c)顶点坐标是(h,k)
(2)抛物线y=a(x-h)2+k与y
=
ax2的关系及平移规律.
2.思想方法方面
用观察、比较、归纳、概括的方法探究二次函数y=a(x-h)2+k的性质;用数形结合思想探究
函数的性质,建立二次函数模型.
(五)作业
课本86页习题3.8第1、2题.
