鲁教版(五四制)九上3.7.1 二次函数与一元二次方程 教案
文档属性
| 名称 | 鲁教版(五四制)九上3.7.1 二次函数与一元二次方程 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 98.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 17:43:15 | ||
图片预览

文档简介
《二次函数与一元二次方程》教学设计
【教学目标】
结合数学课程标准和学科德育一体化要求,围绕“目标—--评价—--教学”一致性原则,确定本课教学目标如下:
1、经历探索二次函数与一元二次方程之间关系的过程,明确二次函数图象与x轴交点的个数与一元二次方程根的个数之间的关系,以及它们分别与△的对应关系。
2、理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c与直线y=h的交点横坐标。
3、通过讨论交流、合作探究等活动,增加学生的数学活动经验,体会类比、数形结合等数学思想,培养数学学科的严谨思维和理性精神。
【教学重点】理解二次函数图象与x轴交点的个数与一元二次方程根的个数之间的关系,以及它们分别与△的对应关系。
【教学难点】理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c与直线y=h的交点横坐标。
【教学过程】
一、情境引入
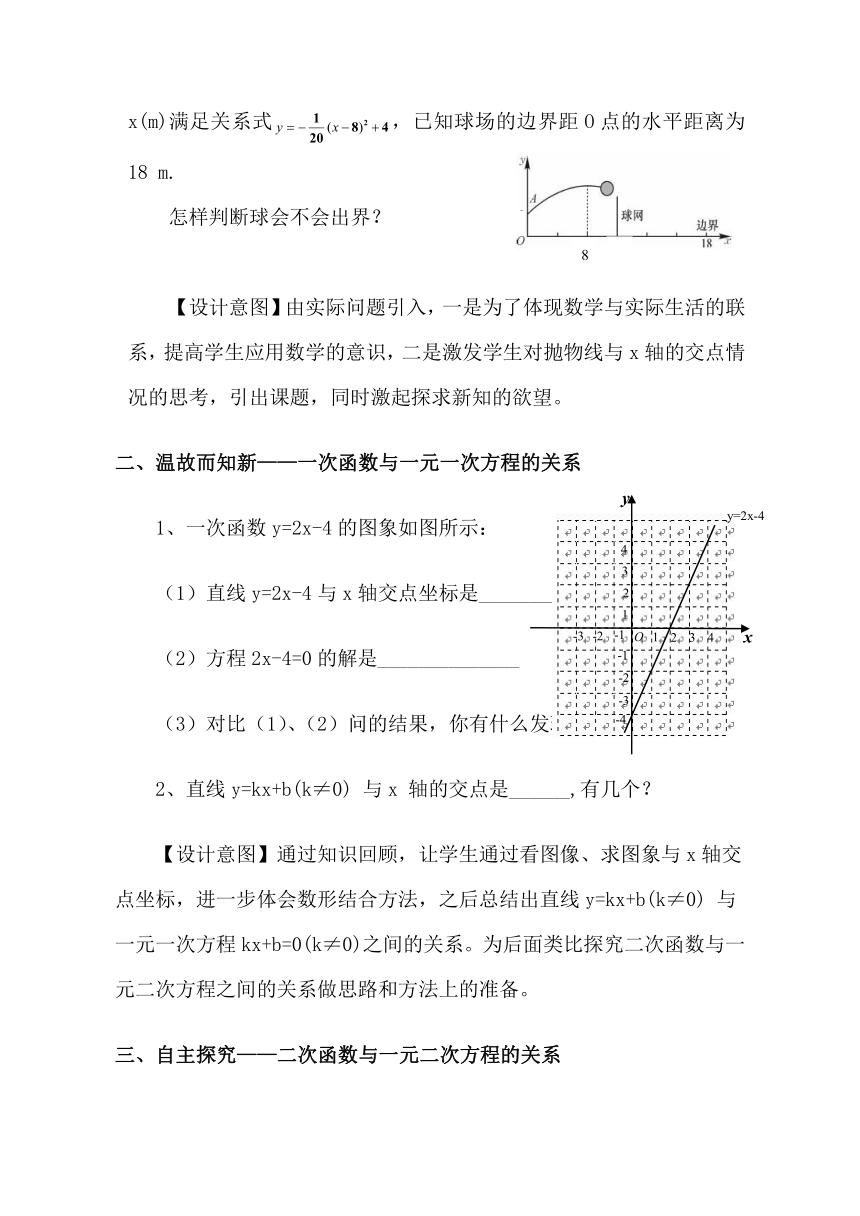
同学们喜欢看排球赛吗?来看下面这个赛场上的问题,你能解决吗?
如图,女排奥运会决赛,塞尔维亚选手站在点O处,将球从正上方的A处发出,如果把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式,已知球场的边界距O点的水平距离为18
m.
怎样判断球会不会出界?
【设计意图】由实际问题引入,一是为了体现数学与实际生活的联系,提高学生应用数学的意识,二是激发学生对抛物线与x轴的交点情况的思考,引出课题,同时激起探求新知的欲望。
二、温故而知新——一次函数与一元一次方程的关系
1、一次函数y=2x-4的图象如图所示:
(1)直线y=2x-4与x轴交点坐标是_________
(2)方程2x-4=0的解是______________
(3)对比(1)、(2)问的结果,你有什么发现?
2、直线y=kx+b(k≠0)
与x
轴的交点是______,有几个?
【设计意图】通过知识回顾,让学生通过看图像、求图象与x轴交点坐标,进一步体会数形结合方法,之后总结出直线y=kx+b(k≠0)
与一元一次方程kx+b=0(k≠0)之间的关系。为后面类比探究二次函数与一元二次方程之间的关系做思路和方法上的准备。
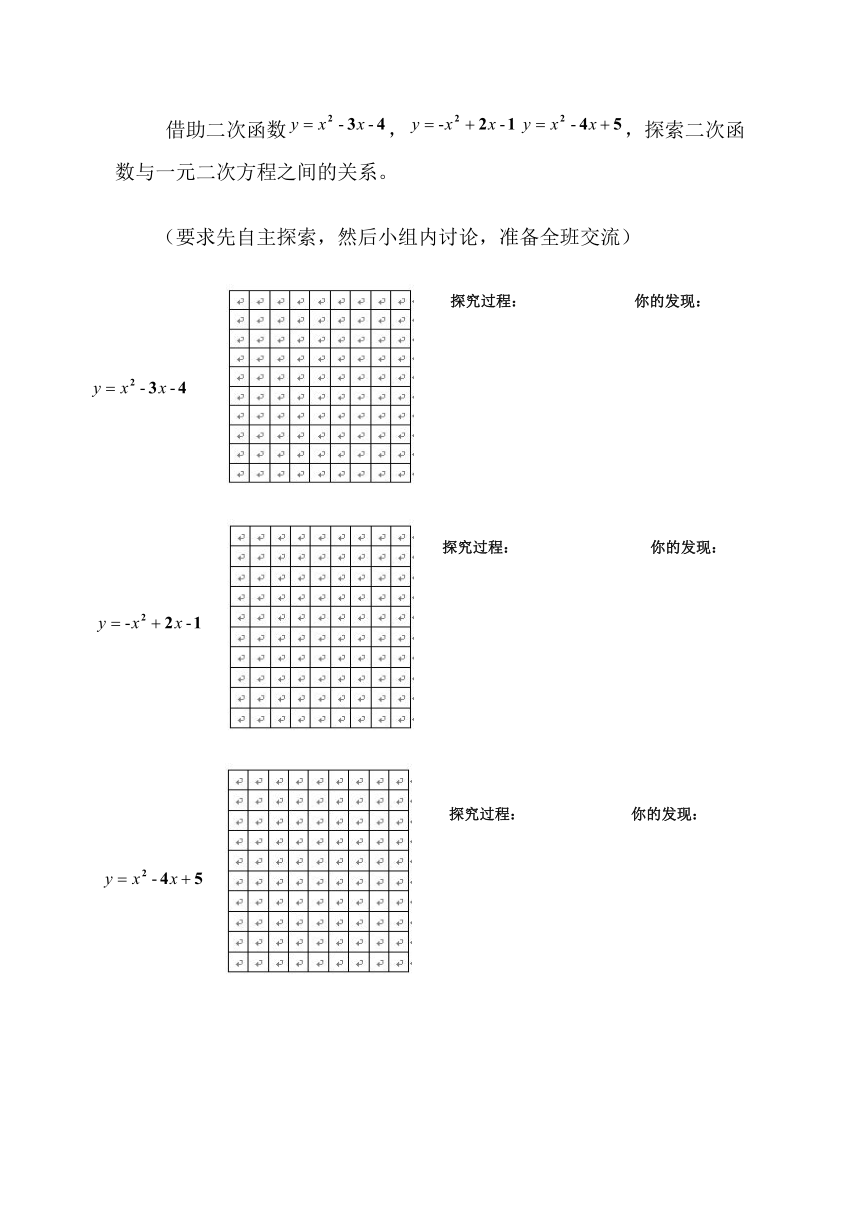
三、自主探究——二次函数与一元二次方程的关系
借助二次函数,,探索二次函数与一元二次方程之间的关系。
(要求先自主探索,然后小组内讨论,准备全班交流)
【设计意图】《数学课程标准》指出:“数学教学,应从学生已有的知识经验出发,让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型,并对此进行解释和应用。”本环节围绕教学目标设计以上探究活动,给学生提供网格和一组二次函数,旨在让学生借助这些学习素材,类比一次函数与一元一次方程的关系,通过小组合作,自主探索,交流展示等活动,最终总结出二次函数与一元二次方程的关系,达成目标1,3。
四、应用拓展
A组
1、下列函数的图象中,与x轴没有公共点的是(
)
2、函数的图象与x轴有___
个交点,交点坐标是
.
3、函数的图象与x轴的交点有
个,交点坐标是
【设计意图】用△直接判断二次函数图象与x轴交点的个数,并会通过解方程求抛物线与x轴交点坐标促进目标2的达成。
B组
1、二次函数图象过(-3,5),且方程ax2+bx+c=0两根分别为x1=
-1,x2=2,求解析式。
2、已知二次函数的图象与x轴有交点,求k的值
【设计意图】第1小题是让学生进一步掌握方程的根就是图象与x轴交点横坐标,根据点的坐标,再求解析式。第2小题意在让学生明确,二次函数图象与x轴交点有坐标,即△≥0,同时注意分析隐含条件:二次函数k≠0,进一步促进目标2达成。
实际应用
现在,你会解决排球问题了吗?来,大家动笔算一下,到底球能不能出界?看看谁最快!有结果了吗?哦,不出界!那么问题来了,怎样阻止进攻呢?有想法的同学可以互相交流一下。我看到有不少同学争执不下,请看下面的这段微视频,能否给你启发?
(播放微视频)
通过刚才的视频,我们可以将前面的结论拓展为:二次函数与直线y=h的交点横坐标x,就是一元二次方程ax2+bx+c=h的根(同时板书上把0改h)
【设计意图】通过实际应用,回归课前问题,第1问是求与x轴交点坐标,学生能够解决,第2问是为了引出求二次函数与直线y=h的交点横坐标x的方法,将x轴拓展到直线y=h,由特殊拓展到一般,促进目标2,3的达成。
C组
1、
函数的图象如图所示,那么关于x的
一元二次方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个异号的实数根
C.有两个相等的实数根
D.没有实数根
2、如图,抛物线y=ax2+bx+c的图象,根据图象回答,
方程ax2+bx+c+3=0的根为_________________
方程ax2+bx+c-1=0的根为_________________
【设计意图】通过这两个练习让学生会结合图象找到满足条件的方程的根,巩固加深对一元二次方程与二次函数之间联系的认识,同时强化学生的数形结合意识,进一步促进目标2,3的达成。
五、反思收获
这节课你学会了哪些知识?掌握了哪些思想、方法?
【设计意图】给学生一个反思的机会,教师引导学生对本节课从内容上和学习方法上去进行归纳总结,使学生对本节课的知识进行及时的巩固,条理化,清晰化。通过总结与反思教会学生整理知识的能力,形成系统的知识体系,养成良好的学习习惯和思考和表达的能力。
六、随堂检测
抛物线y=﹣x2+bx+c的部分图象如图所示,
(1)
0
(2)方程﹣x2+bx+c=0的两根为
(3)若方程﹣x2+bx+c=k有两个相等的实数根,k的取值范围为
【设计意图】通过随堂检测,及时了解学生对本节课知识的理解掌握程度。
8
x
y
O
1
2
y=2x-4
2
1
-3
-2
-1
4
3
-2
4
-4
-3
-1
3
探究过程:
你的发现:
你的发现:
探究过程:
你的发现:
探究过程:
0
3
x
y
【教学目标】
结合数学课程标准和学科德育一体化要求,围绕“目标—--评价—--教学”一致性原则,确定本课教学目标如下:
1、经历探索二次函数与一元二次方程之间关系的过程,明确二次函数图象与x轴交点的个数与一元二次方程根的个数之间的关系,以及它们分别与△的对应关系。
2、理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c与直线y=h的交点横坐标。
3、通过讨论交流、合作探究等活动,增加学生的数学活动经验,体会类比、数形结合等数学思想,培养数学学科的严谨思维和理性精神。
【教学重点】理解二次函数图象与x轴交点的个数与一元二次方程根的个数之间的关系,以及它们分别与△的对应关系。
【教学难点】理解一元二次方程ax2+bx+c=h的根就是二次函数y=ax2+bx+c与直线y=h的交点横坐标。
【教学过程】
一、情境引入
同学们喜欢看排球赛吗?来看下面这个赛场上的问题,你能解决吗?
如图,女排奥运会决赛,塞尔维亚选手站在点O处,将球从正上方的A处发出,如果把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式,已知球场的边界距O点的水平距离为18
m.
怎样判断球会不会出界?
【设计意图】由实际问题引入,一是为了体现数学与实际生活的联系,提高学生应用数学的意识,二是激发学生对抛物线与x轴的交点情况的思考,引出课题,同时激起探求新知的欲望。
二、温故而知新——一次函数与一元一次方程的关系
1、一次函数y=2x-4的图象如图所示:
(1)直线y=2x-4与x轴交点坐标是_________
(2)方程2x-4=0的解是______________
(3)对比(1)、(2)问的结果,你有什么发现?
2、直线y=kx+b(k≠0)
与x
轴的交点是______,有几个?
【设计意图】通过知识回顾,让学生通过看图像、求图象与x轴交点坐标,进一步体会数形结合方法,之后总结出直线y=kx+b(k≠0)
与一元一次方程kx+b=0(k≠0)之间的关系。为后面类比探究二次函数与一元二次方程之间的关系做思路和方法上的准备。
三、自主探究——二次函数与一元二次方程的关系
借助二次函数,,探索二次函数与一元二次方程之间的关系。
(要求先自主探索,然后小组内讨论,准备全班交流)
【设计意图】《数学课程标准》指出:“数学教学,应从学生已有的知识经验出发,让学生亲身经历参与特定的教学活动,获得一些体验,并且通过自主探索,合作交流,将实际问题抽象成数学模型,并对此进行解释和应用。”本环节围绕教学目标设计以上探究活动,给学生提供网格和一组二次函数,旨在让学生借助这些学习素材,类比一次函数与一元一次方程的关系,通过小组合作,自主探索,交流展示等活动,最终总结出二次函数与一元二次方程的关系,达成目标1,3。
四、应用拓展
A组
1、下列函数的图象中,与x轴没有公共点的是(
)
2、函数的图象与x轴有___
个交点,交点坐标是
.
3、函数的图象与x轴的交点有
个,交点坐标是
【设计意图】用△直接判断二次函数图象与x轴交点的个数,并会通过解方程求抛物线与x轴交点坐标促进目标2的达成。
B组
1、二次函数图象过(-3,5),且方程ax2+bx+c=0两根分别为x1=
-1,x2=2,求解析式。
2、已知二次函数的图象与x轴有交点,求k的值
【设计意图】第1小题是让学生进一步掌握方程的根就是图象与x轴交点横坐标,根据点的坐标,再求解析式。第2小题意在让学生明确,二次函数图象与x轴交点有坐标,即△≥0,同时注意分析隐含条件:二次函数k≠0,进一步促进目标2达成。
实际应用
现在,你会解决排球问题了吗?来,大家动笔算一下,到底球能不能出界?看看谁最快!有结果了吗?哦,不出界!那么问题来了,怎样阻止进攻呢?有想法的同学可以互相交流一下。我看到有不少同学争执不下,请看下面的这段微视频,能否给你启发?
(播放微视频)
通过刚才的视频,我们可以将前面的结论拓展为:二次函数与直线y=h的交点横坐标x,就是一元二次方程ax2+bx+c=h的根(同时板书上把0改h)
【设计意图】通过实际应用,回归课前问题,第1问是求与x轴交点坐标,学生能够解决,第2问是为了引出求二次函数与直线y=h的交点横坐标x的方法,将x轴拓展到直线y=h,由特殊拓展到一般,促进目标2,3的达成。
C组
1、
函数的图象如图所示,那么关于x的
一元二次方程的根的情况是(
)
A.有两个不相等的实数根
B.有两个异号的实数根
C.有两个相等的实数根
D.没有实数根
2、如图,抛物线y=ax2+bx+c的图象,根据图象回答,
方程ax2+bx+c+3=0的根为_________________
方程ax2+bx+c-1=0的根为_________________
【设计意图】通过这两个练习让学生会结合图象找到满足条件的方程的根,巩固加深对一元二次方程与二次函数之间联系的认识,同时强化学生的数形结合意识,进一步促进目标2,3的达成。
五、反思收获
这节课你学会了哪些知识?掌握了哪些思想、方法?
【设计意图】给学生一个反思的机会,教师引导学生对本节课从内容上和学习方法上去进行归纳总结,使学生对本节课的知识进行及时的巩固,条理化,清晰化。通过总结与反思教会学生整理知识的能力,形成系统的知识体系,养成良好的学习习惯和思考和表达的能力。
六、随堂检测
抛物线y=﹣x2+bx+c的部分图象如图所示,
(1)
0
(2)方程﹣x2+bx+c=0的两根为
(3)若方程﹣x2+bx+c=k有两个相等的实数根,k的取值范围为
【设计意图】通过随堂检测,及时了解学生对本节课知识的理解掌握程度。
8
x
y
O
1
2
y=2x-4
2
1
-3
-2
-1
4
3
-2
4
-4
-3
-1
3
探究过程:
你的发现:
你的发现:
探究过程:
你的发现:
探究过程:
0
3
x
y
