鲁教版(五四制)九上2.4.1 解直角三角形 教案(表格式)
文档属性
| 名称 | 鲁教版(五四制)九上2.4.1 解直角三角形 教案(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 17:43:15 | ||
图片预览

文档简介
教学课题
解直角三角形(1)
教学目标
知识与技能:理解解直角三角形的含义,会利用已知两边解直角三角形。过程与方法:通过解直角三角形,逐步培养分析问题、解决问题的能力。情感与价值:渗透“数形结合”的数学思想,培养良好的学习习惯。
教学重点与难点
重点:什么是解直角三角形以及已知两边解直角三角形的一般方法。难点:解直角三角形的可解性的解读与认识。
突破措施
几何画板与电子白板的应用
教学方法
自主探索、合作交流
学习方法
小组讨论
教学用具
电子白板
课堂类型
新授
教
学
过
程
一、情景导入
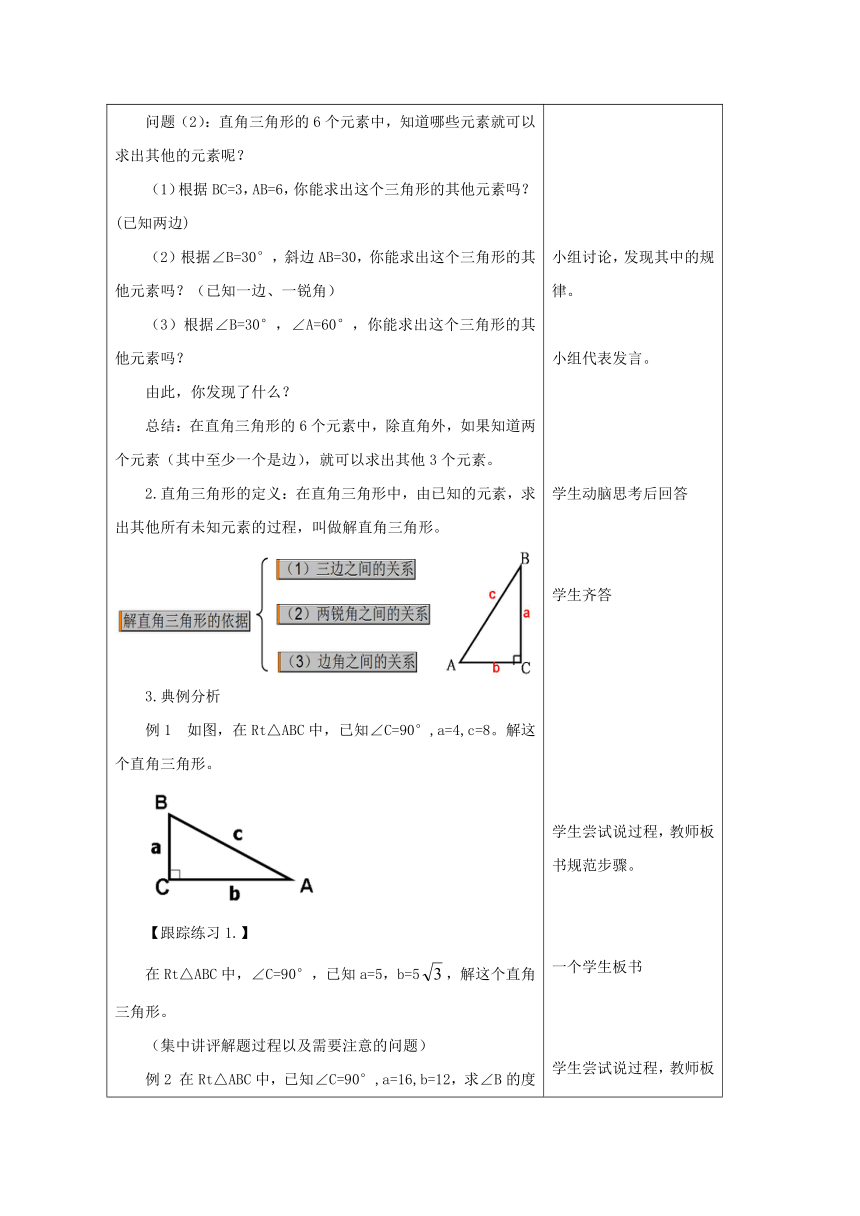
生活中,我们经常会遇到与直角三角形有关的问题,为了解决这些问题,往往需要确定直角三角形的边和角。这节课,我就和同学们一起来探索《解直角三角形》。看到这个题目,同学们有疑问吗?带着这些疑问,我们开始本节课的探索之旅。二、知识回顾1.前面我们学习了锐角三角函数及一些特殊角的三角函数值,请同学们回答:2.计算器在三角函数中的应用:例如:已知sinA=0.9816,求锐角∠A的大小三、探究新知1.问题(1):直角三角形有几条边?几个角?问题(2):直角三角形的6个元素中,知道哪些元素就可以求出其他的元素呢?(1)根据BC=3,AB=6,你能求出这个三角形的其他元素吗?(已知两边)(2)根据∠B=30°,斜边AB=30,你能求出这个三角形的其他元素吗?(已知一边、一锐角)(3)根据∠B=30°,∠A=60°,你能求出这个三角形的其他元素吗?由此,你发现了什么?总结:在直角三角形的6个元素中,除直角外,如果知道两个元素(其中至少一个是边),就可以求出其他3个元素。2.直角三角形的定义:在直角三角形中,由已知的元素,求出其他所有未知元素的过程,叫做解直角三角形。3.典例分析例1
如图,在Rt△ABC中,已知∠C=90°,a=4,c=8。解这个直角三角形。【跟踪练习1.】在Rt△ABC中,∠C=90°,已知a=5,b=5,解这个直角三角形。(集中讲评解题过程以及需要注意的问题)例2
在Rt△ABC中,已知∠C=90°,a=16,b=12,求∠B的度数(结果精确到1°)和c的长。
【跟踪练习2.】在Rt△ABC中,∠C=90°,已知c=26,b=24,求a的长和∠B的度数(结果精确到1')。(可借助计算器)(集中讲评解题过程以及需要注意的问题)课堂检测在Rt△ABC中,已知∠C=90°,a=,b=。解这个直角三角形。(2)
在Rt△ABC中,已知∠C=90°,b=6,c=8。解这个直角三角形。(可借助计算器)(掌声鼓励做对同学,希望更多的同学表现出色)四、课堂小结你能总结一下已知两边解直角三角形的过程吗?与同伴进行交流。①画一个直角三角形,标上已知元素。②利用勾股定理求出第三边。③利用已知两边所对应的三角函数值,求出一锐角。④利用“直角三角形的两锐角互余”求出另一锐角。(教师进行补充)五、拓展提高
如图,等腰△ABC的底边长BC=20,面积为100,求这个三角形各角的大小和腰长。六、谈收获
请你谈谈,本节课你有哪些收获?
1.什么是解直角三角形2.已知两边解直角三角形的过程3.“数形结合”数学思想的运用
学
生
活
动有疑问的同学举手回答。随机选取9个同学进行回答。学生拿出手中的计算器,算一下∠A的大小,一个同学回答按键顺序。小组讨论,发现其中的规律。小组代表发言。学生动脑思考后回答学生齐答学生尝试说过程,教师板书规范步骤。一个学生板书学生尝试说过程,教师板书规范步骤。一个学生板书学生动笔练习,小组讨论纠错。同桌交流,学生回答学生动脑思考,一个学生到讲台讲解。学生思考,举手回答。
解直角三角形(1)
教学目标
知识与技能:理解解直角三角形的含义,会利用已知两边解直角三角形。过程与方法:通过解直角三角形,逐步培养分析问题、解决问题的能力。情感与价值:渗透“数形结合”的数学思想,培养良好的学习习惯。
教学重点与难点
重点:什么是解直角三角形以及已知两边解直角三角形的一般方法。难点:解直角三角形的可解性的解读与认识。
突破措施
几何画板与电子白板的应用
教学方法
自主探索、合作交流
学习方法
小组讨论
教学用具
电子白板
课堂类型
新授
教
学
过
程
一、情景导入
生活中,我们经常会遇到与直角三角形有关的问题,为了解决这些问题,往往需要确定直角三角形的边和角。这节课,我就和同学们一起来探索《解直角三角形》。看到这个题目,同学们有疑问吗?带着这些疑问,我们开始本节课的探索之旅。二、知识回顾1.前面我们学习了锐角三角函数及一些特殊角的三角函数值,请同学们回答:2.计算器在三角函数中的应用:例如:已知sinA=0.9816,求锐角∠A的大小三、探究新知1.问题(1):直角三角形有几条边?几个角?问题(2):直角三角形的6个元素中,知道哪些元素就可以求出其他的元素呢?(1)根据BC=3,AB=6,你能求出这个三角形的其他元素吗?(已知两边)(2)根据∠B=30°,斜边AB=30,你能求出这个三角形的其他元素吗?(已知一边、一锐角)(3)根据∠B=30°,∠A=60°,你能求出这个三角形的其他元素吗?由此,你发现了什么?总结:在直角三角形的6个元素中,除直角外,如果知道两个元素(其中至少一个是边),就可以求出其他3个元素。2.直角三角形的定义:在直角三角形中,由已知的元素,求出其他所有未知元素的过程,叫做解直角三角形。3.典例分析例1
如图,在Rt△ABC中,已知∠C=90°,a=4,c=8。解这个直角三角形。【跟踪练习1.】在Rt△ABC中,∠C=90°,已知a=5,b=5,解这个直角三角形。(集中讲评解题过程以及需要注意的问题)例2
在Rt△ABC中,已知∠C=90°,a=16,b=12,求∠B的度数(结果精确到1°)和c的长。
【跟踪练习2.】在Rt△ABC中,∠C=90°,已知c=26,b=24,求a的长和∠B的度数(结果精确到1')。(可借助计算器)(集中讲评解题过程以及需要注意的问题)课堂检测在Rt△ABC中,已知∠C=90°,a=,b=。解这个直角三角形。(2)
在Rt△ABC中,已知∠C=90°,b=6,c=8。解这个直角三角形。(可借助计算器)(掌声鼓励做对同学,希望更多的同学表现出色)四、课堂小结你能总结一下已知两边解直角三角形的过程吗?与同伴进行交流。①画一个直角三角形,标上已知元素。②利用勾股定理求出第三边。③利用已知两边所对应的三角函数值,求出一锐角。④利用“直角三角形的两锐角互余”求出另一锐角。(教师进行补充)五、拓展提高
如图,等腰△ABC的底边长BC=20,面积为100,求这个三角形各角的大小和腰长。六、谈收获
请你谈谈,本节课你有哪些收获?
1.什么是解直角三角形2.已知两边解直角三角形的过程3.“数形结合”数学思想的运用
学
生
活
动有疑问的同学举手回答。随机选取9个同学进行回答。学生拿出手中的计算器,算一下∠A的大小,一个同学回答按键顺序。小组讨论,发现其中的规律。小组代表发言。学生动脑思考后回答学生齐答学生尝试说过程,教师板书规范步骤。一个学生板书学生尝试说过程,教师板书规范步骤。一个学生板书学生动笔练习,小组讨论纠错。同桌交流,学生回答学生动脑思考,一个学生到讲台讲解。学生思考,举手回答。
