鲁教版(五四制)九上2.6 利用三角函数测高 教案
文档属性
| 名称 | 鲁教版(五四制)九上2.6 利用三角函数测高 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 968.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-01 17:43:15 | ||
图片预览

文档简介
利用三角函数测高
教学设计
教学目标:
1.
知识与能力:经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程。
2.
过程与方法:能够对所得到的数据进行分析,能够对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果。能够综合运用直角三角形边角关系的知识解决实际问题。
3.
情感、态度与价值观:培养不怕困难的品质,发展合作意识和科学精神。
教学重点:
自制测角仪,设计活动方案,测量实际物体的高度。
教学难点:
测量仰角,测量距离,画出测量示意图,写出计算过程。
教学过程:
1、测角仪的使用
转动转盘,使度盘的直径对准目标M,记下此时水平线所指的度数。
2、活动一
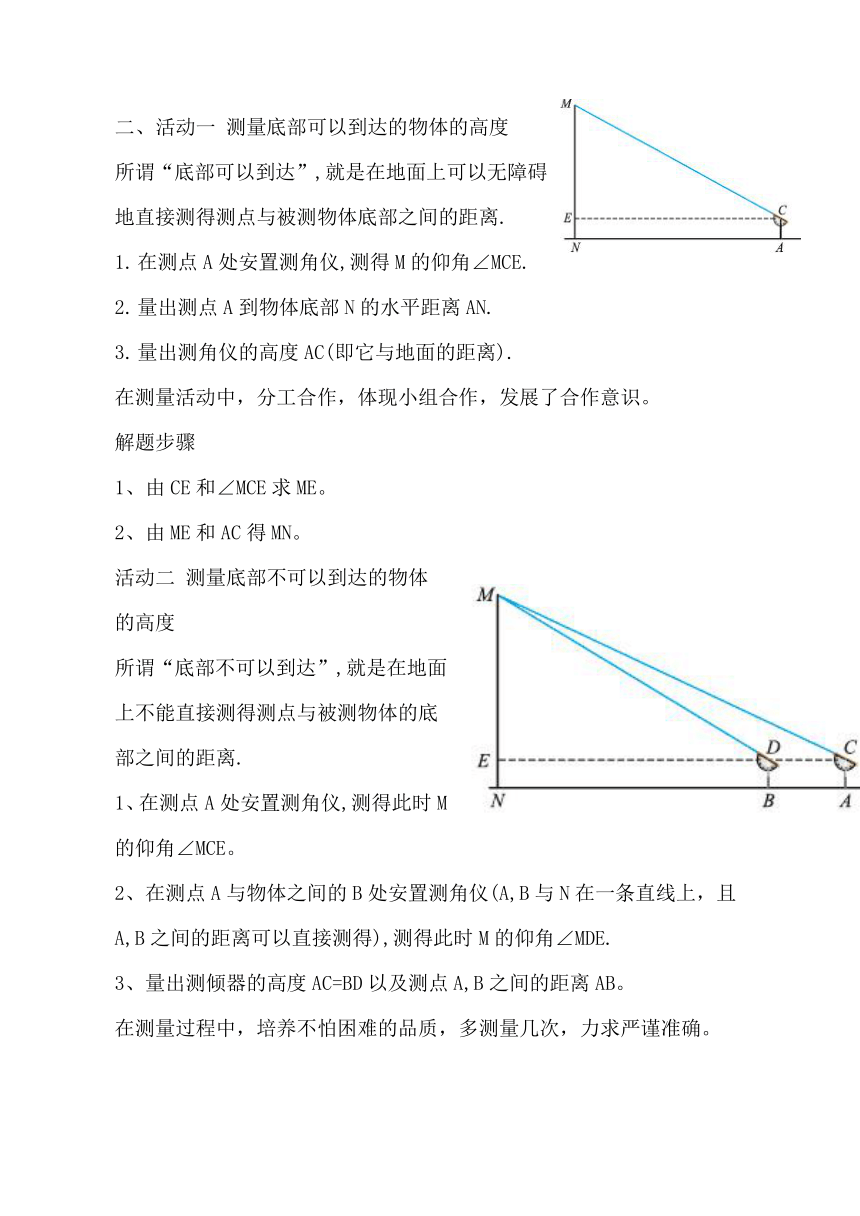
测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
1.
在测点A处安置测角仪,测得M的仰角∠MCE.
2.
量出测点A到物体底部N的水平距离AN.
3.
量出测角仪的高度AC(即它与地面的距离).
在测量活动中,分工合作,体现小组合作,发展了合作意识。
解题步骤
1、由CE和∠MCE求ME。
2、由ME和AC得MN。
活动二
测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
1、在测点A处安置测角仪,测得此时M的仰角∠MCE。
2、在测点A与物体之间的B处安置测角仪(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE.
3、量出测倾器的高度AC=BD以及测点A,B之间的距离AB。
在测量过程中,培养不怕困难的品质,多测量几次,力求严谨准确。
解题步骤:
1、利用∠MCE和∠MDE以及CD的长度分别解直角三角形。
2、解以ME为未知数的一元一次方程。
3、由ME求MN。
三、当堂检测:
1、如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.
2、河对岸的高层建筑AB,为测量其高,在C处由D点用测量仪测得顶端A的仰角为30?,向高层建筑物前进50m到达C?处,由D?测得顶端A的仰角为45?,已知测量仪CD=C?D?=1.2m,求建筑物AB的高。
四、教学反思
各小组根据计算数据展开讨论,为什么计算结果有差距,产生差距的原因是什么。通过本节课,旨在使学生学会使用三角函数测高,并在活动过程中体会严谨的科学态度,通过计算产生的差距分析误差产生的原因,培养学生客观真实追求完美的思想品质。本节课让学生学会建立直角三角形模型解决实际问题,利用直角三角形的边角关系测高。
D
C
A
B
C/
教学设计
教学目标:
1.
知识与能力:经历设计活动方案、自制仪器或运用仪器进行实地测量以及撰写活动报告的过程。
2.
过程与方法:能够对所得到的数据进行分析,能够对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果。能够综合运用直角三角形边角关系的知识解决实际问题。
3.
情感、态度与价值观:培养不怕困难的品质,发展合作意识和科学精神。
教学重点:
自制测角仪,设计活动方案,测量实际物体的高度。
教学难点:
测量仰角,测量距离,画出测量示意图,写出计算过程。
教学过程:
1、测角仪的使用
转动转盘,使度盘的直径对准目标M,记下此时水平线所指的度数。
2、活动一
测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离.
1.
在测点A处安置测角仪,测得M的仰角∠MCE.
2.
量出测点A到物体底部N的水平距离AN.
3.
量出测角仪的高度AC(即它与地面的距离).
在测量活动中,分工合作,体现小组合作,发展了合作意识。
解题步骤
1、由CE和∠MCE求ME。
2、由ME和AC得MN。
活动二
测量底部不可以到达的物体的高度
所谓“底部不可以到达”,就是在地面上不能直接测得测点与被测物体的底部之间的距离.
1、在测点A处安置测角仪,测得此时M的仰角∠MCE。
2、在测点A与物体之间的B处安置测角仪(A,B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE.
3、量出测倾器的高度AC=BD以及测点A,B之间的距离AB。
在测量过程中,培养不怕困难的品质,多测量几次,力求严谨准确。
解题步骤:
1、利用∠MCE和∠MDE以及CD的长度分别解直角三角形。
2、解以ME为未知数的一元一次方程。
3、由ME求MN。
三、当堂检测:
1、如图,在离铁塔150米的A处,用测角仪测得塔顶的仰角为30°,已知测角仪高AD=1.5米,求铁塔高BE.
2、河对岸的高层建筑AB,为测量其高,在C处由D点用测量仪测得顶端A的仰角为30?,向高层建筑物前进50m到达C?处,由D?测得顶端A的仰角为45?,已知测量仪CD=C?D?=1.2m,求建筑物AB的高。
四、教学反思
各小组根据计算数据展开讨论,为什么计算结果有差距,产生差距的原因是什么。通过本节课,旨在使学生学会使用三角函数测高,并在活动过程中体会严谨的科学态度,通过计算产生的差距分析误差产生的原因,培养学生客观真实追求完美的思想品质。本节课让学生学会建立直角三角形模型解决实际问题,利用直角三角形的边角关系测高。
D
C
A
B
C/
