11.1.2《三角形的高、中线与角平分线》课件2021--2022学年人教版八年级数学上册(38张)
文档属性
| 名称 | 11.1.2《三角形的高、中线与角平分线》课件2021--2022学年人教版八年级数学上册(38张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 644.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 12:02:18 | ||
图片预览









文档简介
(共38张PPT)
11.1.2
三角形的高、中线与角平分线
八年级上册
学习目标
1
2
理解三角形的高、中线、角平分线,以及三角形的重心等概念,并会用工具准确画出三角形的三条主要线段
在由图叙述定义的过程中,培养严谨的语言表达能力
3
在画图过程中,培养观察能力,从中发现新知,激发探索欲
学习重难点
重点
难点
三角形的高、中线、角平分线的定义及画法
三角形的高、中线、角平分线的定义及画法
预习检测
什么是三角形的高?
什么是三角形的中线?
什么是三角形的重心?
什么是三角形的角平分线?
问题1 与三角形有关的线段,除了三条边,还有三角形的高.过三角形的一个顶点,你能画出它的对边的垂线吗?
探究一、三角形的高
课堂探究
课堂探究
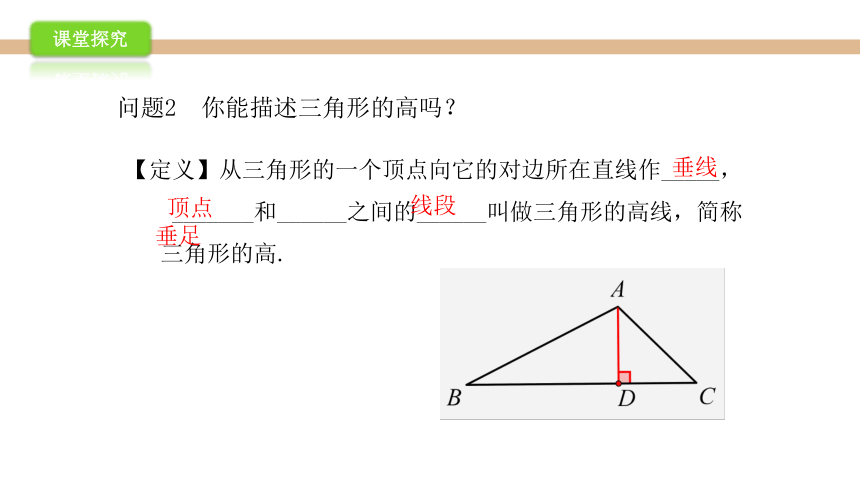
【定义】从三角形的一个顶点向它的对边所在直线作_____,
_______和______之间的______叫做三角形的高线,简称
三角形的高.
垂线
顶点
垂足
线段
问题2 你能描述三角形的高吗?
课堂探究
∵AD是△ABC的高
反之,
如图
(
)
,(已知)
∴AD⊥BC(∠BDA
=90°).
∵AD⊥BC(∠BDA=90°),
(已知)
∴AD是△ABC的高.
(
)
符号语言
三角形的高线定义
三角形的高线定义
问题3 分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
锐角三角形的三条高都在三角形的内部;
直角三角形的两条高分别与两条边重合;
钝角三角形的两条高在三角形的外部.
三角形三条高所在的直线交于一点.
课堂探究
每个人画一个锐角三角形纸片。
(1)
你能画出这个三角形的三条高吗?
(2)
你能用折纸的办法找到吗?
(3)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
动手做一做
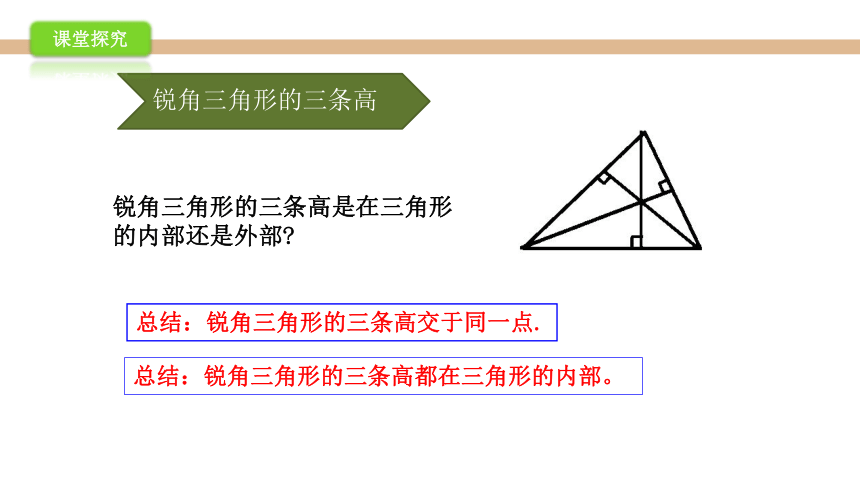
锐角三角形的三条高
锐角三角形的三条高是在三角形的内部还是外部?
总结:锐角三角形的三条高交于同一点.
总结:锐角三角形的三条高都在三角形的内部。
课堂探究
在纸上画出一个直角三角形。
画出直角三角形的三条高,它们有怎样的位置关系?将你的结果与同伴进行交流.
动手做一做
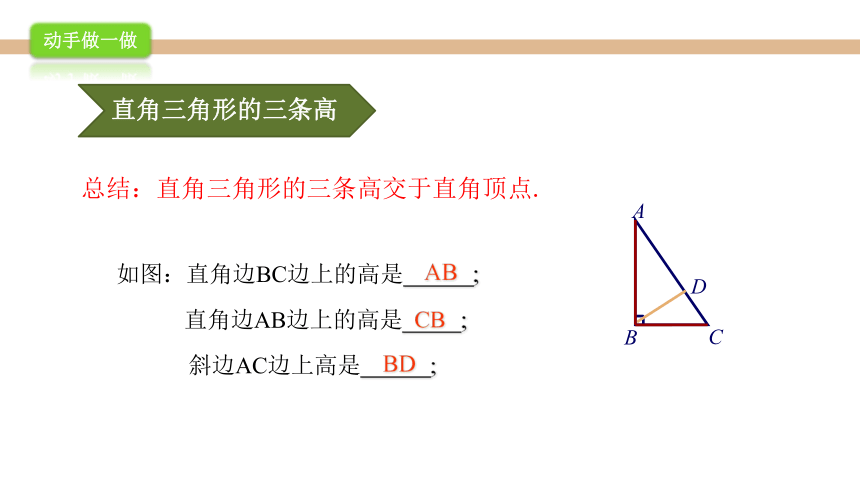
直角三角形的三条高
总结:直角三角形的三条高交于直角顶点.
如图:直角边BC边上的高是
;
直角边AB边上的高是
;
斜边AC边上高是
;
AB
CB
BD
动手做一做
A
B
C
D
议一议:
钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
课堂探究
钝角三角形的三条高
总结:钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
课堂探究
A
B
C
D
E
F
三角形的三条高的特性:
锐角三角形
直角三角形
钝角三角形
高在三角形内部的数量
3
1
1
高之间是否相交
相交
相交
不相交
高所在的直线是否相交
相交
相交
相交
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
课堂探究
C
例1、在下图中,正确画出△ABC
中边BC
上高的是(
)
(
A
)
(
B
)
(
C)
(
D
)
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
典例精析
(2)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角三角形
(1)AD为三角形ABC的高,则∠ADB=
=_____.
练一练
B
(3)如图,△ABC中,AD⊥BC于D,则
S△ABC
=
BC?AD
,
S△ABD=
,
S△ADC=
,
那么,
S△ABD
:
S△ADC=
.
BD?AD
DC?AD
BD
:
DC
练一练
S△ABD=
,
如图,△ABC中,若D是BC边上一点,则
BD
:
DC
?
想到:过A点作AE⊥BC于点E,则
S△ABD
:
S△ADC=
S△ADC=
.
BD?AE
DC?AE
练一练
问题4 刚才我们学习了三角形的高,小学我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
探究二、三角形的中线
课堂探究
如图,△ABC中,若D是BC边上一点,则
BD
:
DC
当BD=DC时,两三角形的面积相等,
即点D是BC的中点,那么此时的AD就叫做△ABC的中线.
S△ABD
:
S△ADC=
.
【定义】在三角形中,连接一个______与它____________的线段,叫做三角形的中线.
顶点
对边的中点
课堂探究
∵AD是△ABC的中线
反之,如图
(三角形的中线定义)
,(已知)
∴AD是△ABC的中线.
(三角形的中线定义)
∵BD=DC=
BC,
符号语言
(已知)
∴BD=DC=
BC.
课堂探究
问题5 如上图,画出△ABC
的另两条中线,观察三条中线,你有什么发现?
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
课堂探究
A
B
C
D
2
2
BD
6
cm?
例2 如图,AD,BE,CF
是△ABC
的三条中线.
(1)AC
=
AE
=
EC;CD
=
;
AF
=
AB;
(2)若S△ABC=12
cm2,
则S△ABD=
.
A
B
C
D
E
F
G
例题解析
在△ABC中,当D点在BC边上运动时,可得到AD是△ABC的高,AD是△ABC的中线,AD还会有什么特殊的位置呢?
课堂探究
探究三、三角形的角平分线
问题6 准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕BD把∠ABC
分成∠1和∠2两个角.∠1和∠2有什么关系?
A
B
C
D
B
C
A
A
B
C
D
1
2
课堂探究
【定义】在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
1
2
课堂探究
∵AD是△ABC的角平分线,
反之,如图
∴AD是△ABC的角平分线.
符号语言
∴∠1=∠2=
∠BAC.
1
2
∵∠1=∠2=
∠BAC
,
(已知)
(三角形角平分线定义)
(三角形角平分线定义)
(已知)
课堂探究
问题7 如上图,画出△ABC
的另两条角平分线,观察三条角平分线,你有什么发现?
三角形的三条角平分线相交于一点.
课堂探究
∠2
例3 如图,AD,BE,CF
是△ABC
的三条角平分线,则:
∠1
=
;
∠3
=
;
∠ACB
=
2
.
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
典例精析
1、如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180使点B
落在点B′的位置,则线段AC是(
)
A.边BB′上的中线
B.边BB′上的高
C.∠BAB′的角平分线
D.以上答案都正确
练一练
2.如图,已知AD,AE分别为三角形ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°,
试求:
(1)△ABE的面积;
(2)△ACE和△ABE的周长的差。
练一练
课堂练习
1、下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
课堂练习
2、在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.正确的是( )
A.①②
B.③④
C.①④
D.②③
3、AD是△ABC的一条高,如果∠BAD=65°,∠CAD=30°,则∠BAC=__________.
D
95°或35°
课堂小结
1
2
1.三角形的高、中线、角平分线都在三角形的内部吗?
2.三角形的高、中线、角平分线都是直线吗?
3.三角形的角平分线与角的角平分线一样吗?
4.直角三角形的两条直角边也是三角形的高吗?
5.
三角形的三条中线交于一点,这个交点叫做这个三角形的
.
课后作业
1.
如图,在△ABC中,AE是中线,AD是角平分线,AF是高.填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°
;
(4)
若S△ABD
=9,则S△ABC
=
.
课后作业
2.如图,在?△ABC??中,
AB=2,BC=4.?△ABC的高AD?与?CE的比是多少?(提示:利用三角形的面积公式.)
课后作业
3.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF.
画高DG,EH,FM.
画角平分线
GM,HN,KP.
11.1.2
三角形的高、中线与角平分线
八年级上册
学习目标
1
2
理解三角形的高、中线、角平分线,以及三角形的重心等概念,并会用工具准确画出三角形的三条主要线段
在由图叙述定义的过程中,培养严谨的语言表达能力
3
在画图过程中,培养观察能力,从中发现新知,激发探索欲
学习重难点
重点
难点
三角形的高、中线、角平分线的定义及画法
三角形的高、中线、角平分线的定义及画法
预习检测
什么是三角形的高?
什么是三角形的中线?
什么是三角形的重心?
什么是三角形的角平分线?
问题1 与三角形有关的线段,除了三条边,还有三角形的高.过三角形的一个顶点,你能画出它的对边的垂线吗?
探究一、三角形的高
课堂探究
课堂探究
【定义】从三角形的一个顶点向它的对边所在直线作_____,
_______和______之间的______叫做三角形的高线,简称
三角形的高.
垂线
顶点
垂足
线段
问题2 你能描述三角形的高吗?
课堂探究
∵AD是△ABC的高
反之,
如图
(
)
,(已知)
∴AD⊥BC(∠BDA
=90°).
∵AD⊥BC(∠BDA=90°),
(已知)
∴AD是△ABC的高.
(
)
符号语言
三角形的高线定义
三角形的高线定义
问题3 分别画一个锐角三角形、直角三角形、钝角三角形,你能分别画出这三个三角形的三条高吗?
锐角三角形的三条高都在三角形的内部;
直角三角形的两条高分别与两条边重合;
钝角三角形的两条高在三角形的外部.
三角形三条高所在的直线交于一点.
课堂探究
每个人画一个锐角三角形纸片。
(1)
你能画出这个三角形的三条高吗?
(2)
你能用折纸的办法找到吗?
(3)
这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
动手做一做
锐角三角形的三条高
锐角三角形的三条高是在三角形的内部还是外部?
总结:锐角三角形的三条高交于同一点.
总结:锐角三角形的三条高都在三角形的内部。
课堂探究
在纸上画出一个直角三角形。
画出直角三角形的三条高,它们有怎样的位置关系?将你的结果与同伴进行交流.
动手做一做
直角三角形的三条高
总结:直角三角形的三条高交于直角顶点.
如图:直角边BC边上的高是
;
直角边AB边上的高是
;
斜边AC边上高是
;
AB
CB
BD
动手做一做
A
B
C
D
议一议:
钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?
将你的结果与同伴进行交流.
课堂探究
钝角三角形的三条高
总结:钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
课堂探究
A
B
C
D
E
F
三角形的三条高的特性:
锐角三角形
直角三角形
钝角三角形
高在三角形内部的数量
3
1
1
高之间是否相交
相交
相交
不相交
高所在的直线是否相交
相交
相交
相交
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
课堂探究
C
例1、在下图中,正确画出△ABC
中边BC
上高的是(
)
(
A
)
(
B
)
(
C)
(
D
)
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
典例精析
(2)如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是(
)
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角三角形
(1)AD为三角形ABC的高,则∠ADB=
=_____.
练一练
B
(3)如图,△ABC中,AD⊥BC于D,则
S△ABC
=
BC?AD
,
S△ABD=
,
S△ADC=
,
那么,
S△ABD
:
S△ADC=
.
BD?AD
DC?AD
BD
:
DC
练一练
S△ABD=
,
如图,△ABC中,若D是BC边上一点,则
BD
:
DC
?
想到:过A点作AE⊥BC于点E,则
S△ABD
:
S△ADC=
S△ADC=
.
BD?AE
DC?AE
练一练
问题4 刚才我们学习了三角形的高,小学我们已经知道了三角形的面积公式,你能经过三角形的一个顶点画一条线段,将这个三角形分为面积相等的两个三角形吗?
探究二、三角形的中线
课堂探究
如图,△ABC中,若D是BC边上一点,则
BD
:
DC
当BD=DC时,两三角形的面积相等,
即点D是BC的中点,那么此时的AD就叫做△ABC的中线.
S△ABD
:
S△ADC=
.
【定义】在三角形中,连接一个______与它____________的线段,叫做三角形的中线.
顶点
对边的中点
课堂探究
∵AD是△ABC的中线
反之,如图
(三角形的中线定义)
,(已知)
∴AD是△ABC的中线.
(三角形的中线定义)
∵BD=DC=
BC,
符号语言
(已知)
∴BD=DC=
BC.
课堂探究
问题5 如上图,画出△ABC
的另两条中线,观察三条中线,你有什么发现?
三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
课堂探究
A
B
C
D
2
2
BD
6
cm?
例2 如图,AD,BE,CF
是△ABC
的三条中线.
(1)AC
=
AE
=
EC;CD
=
;
AF
=
AB;
(2)若S△ABC=12
cm2,
则S△ABD=
.
A
B
C
D
E
F
G
例题解析
在△ABC中,当D点在BC边上运动时,可得到AD是△ABC的高,AD是△ABC的中线,AD还会有什么特殊的位置呢?
课堂探究
探究三、三角形的角平分线
问题6 准备一个三角形纸片ABC,按图所示的方法折叠,展开后,折痕BD把∠ABC
分成∠1和∠2两个角.∠1和∠2有什么关系?
A
B
C
D
B
C
A
A
B
C
D
1
2
课堂探究
【定义】在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线.
1
2
课堂探究
∵AD是△ABC的角平分线,
反之,如图
∴AD是△ABC的角平分线.
符号语言
∴∠1=∠2=
∠BAC.
1
2
∵∠1=∠2=
∠BAC
,
(已知)
(三角形角平分线定义)
(三角形角平分线定义)
(已知)
课堂探究
问题7 如上图,画出△ABC
的另两条角平分线,观察三条角平分线,你有什么发现?
三角形的三条角平分线相交于一点.
课堂探究
∠2
例3 如图,AD,BE,CF
是△ABC
的三条角平分线,则:
∠1
=
;
∠3
=
;
∠ACB
=
2
.
∠ABC
∠4
A
B
C
D
E
F
1
2
3
4
典例精析
1、如图所示,在△ABC中,∠ACB=90°,把△ABC沿直线AC翻折180使点B
落在点B′的位置,则线段AC是(
)
A.边BB′上的中线
B.边BB′上的高
C.∠BAB′的角平分线
D.以上答案都正确
练一练
2.如图,已知AD,AE分别为三角形ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°,
试求:
(1)△ABE的面积;
(2)△ACE和△ABE的周长的差。
练一练
课堂练习
1、下列说法正确的是( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可能在三角形外
D.三角形的角平分线是射线
B
课堂练习
2、在△ABC中,AD为中线,BE为角平分线,则在以下等式中:①∠BAD=∠CAD;②∠ABE=∠CBE;③BD=DC;④AE=EC.正确的是( )
A.①②
B.③④
C.①④
D.②③
3、AD是△ABC的一条高,如果∠BAD=65°,∠CAD=30°,则∠BAC=__________.
D
95°或35°
课堂小结
1
2
1.三角形的高、中线、角平分线都在三角形的内部吗?
2.三角形的高、中线、角平分线都是直线吗?
3.三角形的角平分线与角的角平分线一样吗?
4.直角三角形的两条直角边也是三角形的高吗?
5.
三角形的三条中线交于一点,这个交点叫做这个三角形的
.
课后作业
1.
如图,在△ABC中,AE是中线,AD是角平分线,AF是高.填空:
(1)BE=
=
;
(2)∠BAD=
=
;
(3)∠AFB=
=90°
;
(4)
若S△ABD
=9,则S△ABC
=
.
课后作业
2.如图,在?△ABC??中,
AB=2,BC=4.?△ABC的高AD?与?CE的比是多少?(提示:利用三角形的面积公式.)
课后作业
3.按要求画出下列三角形的中线、高线、角平分线.
画中线AD,BE,CF.
画高DG,EH,FM.
画角平分线
GM,HN,KP.
