21.2.2.1《公式法解一元二次方程》课件2021--2022学年人教版九年级数学上册(25张)
文档属性
| 名称 | 21.2.2.1《公式法解一元二次方程》课件2021--2022学年人教版九年级数学上册(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 341.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 12:04:00 | ||
图片预览








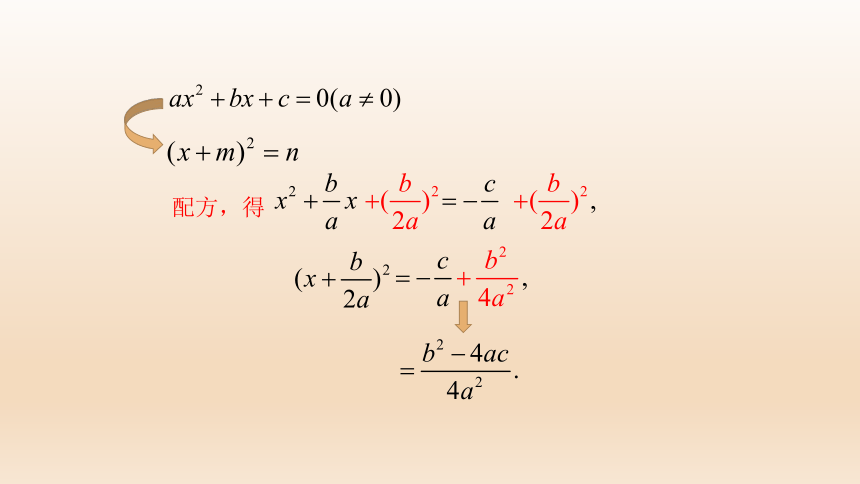
文档简介
(共25张PPT)
21.2.2.1
公式法解一元二次方程
九年级上册
学习目标
1
2
了解一元二次方程的求根公式的推导过程
加深对求根公式的认识的同时,培养学生的运算能力,推理能力和分类讨论的意识.
学习重难点
重点
难点
一元二次方程求根公式的推导
用配方法解字母系数的一元二次方程
预习检测
你能推导出方程一元二次方程ax2+bx+c=0的求根公式吗?
问题1
请回顾,在前面的学习中,学过哪些解一元二次方程的方法.
直接开平方法
配方法
转化
复习回顾
问题2
用配方法解方程5x2-3x=x+1.
解:5x2-4x=1.
二次项系数化为1,得
配方,得
由此可得
问题3
你能不能也用配方法求出关于x的一元二次方程ax2+bx+c=0(a≠0)的解呢?
探究新知
解:
移项,得
二次项系数化为1,得
配方,得
一次项系数
一半的平方
因为(a≠0)
根据等式性质
配方,得
配方,得
由
性质
由
性质
所以方程无实数根.
总结
方程有两个相等实数根
关于x的一元二次方程ax2+bx+c=0(a≠0)的根的情况:
方程有两个不相等实数根
方程无实数根.
可见,式子b2-4ac决定了一元二次方程的根的情况.
当b2-4ac>0及b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)的实数根可写为
的形式.
当b2-4ac≥0时,方程ax2+bx+c=0(a≠0)的实数根可写为
的形式,这个式子叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式.
解一元二次方程时,把各系数直接代入求根公式,这种解一元二次方程的方法叫做公式法.
一元二次方程ax2+bx+c=0(a≠0)的解法
直接开平方法
配方法
公式法
例
用公式法解方程5x2-3x=x+1.
解:方程化为5x2-4x-1=0.
方程有两个不相等实数根
即:
巩固落实
(1)化
“一般形式”.
(2)确定a,b,c(注意符号).
(3)计算b2-4ac的值.
(4)当b2-4ac≥0时
,将a,b,c及b2-4ac代入公式
(5)结果化成最简形式.
用公式法解一元二次方程的一般步骤
当b2-4ac<0时
,方程无实数根.
公式法
解:
方程有两个不相等实数根
配方法
问题4
比较两种解法,能体会出为什么学习公式法吗?
①利用配方法可以推导出求根公式,配方是推
导求根公式的中间过程.
②公式法则省去了配方的中间过程,直接利用了配方的结果.
③公式法的优点是操作简单,直接计算,是解一元二次方程的通法.
课堂练习
1.一元二次方程x2-4x+5=0的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
D
课堂练习
2.已知A=a+2,B=a2-a+5,C=a2+5a+19.
(1)求证:B-A>0;
(2)指出A与C哪个大?并说明理由.
解:(1)B-A=(a-1)2+2>0
(2)C-A=(a+2)2+13>0,∴C>A
用公式法解一元二次方程的“四个步骤”:
(1)
把一元二次方程化为一般形式.
(2)
确定a,b,c的值.
(3)
计算b2-4ac的值.
(4)
当b2-4ac≥0时,把a,b,c的值代入求根公式,求出方程的两个实数根;
当b2-4ac<0时,方程无实数根.
课堂小结
用公式法解下列方程:
课后作业
21.2.2.1
公式法解一元二次方程
九年级上册
学习目标
1
2
了解一元二次方程的求根公式的推导过程
加深对求根公式的认识的同时,培养学生的运算能力,推理能力和分类讨论的意识.
学习重难点
重点
难点
一元二次方程求根公式的推导
用配方法解字母系数的一元二次方程
预习检测
你能推导出方程一元二次方程ax2+bx+c=0的求根公式吗?
问题1
请回顾,在前面的学习中,学过哪些解一元二次方程的方法.
直接开平方法
配方法
转化
复习回顾
问题2
用配方法解方程5x2-3x=x+1.
解:5x2-4x=1.
二次项系数化为1,得
配方,得
由此可得
问题3
你能不能也用配方法求出关于x的一元二次方程ax2+bx+c=0(a≠0)的解呢?
探究新知
解:
移项,得
二次项系数化为1,得
配方,得
一次项系数
一半的平方
因为(a≠0)
根据等式性质
配方,得
配方,得
由
性质
由
性质
所以方程无实数根.
总结
方程有两个相等实数根
关于x的一元二次方程ax2+bx+c=0(a≠0)的根的情况:
方程有两个不相等实数根
方程无实数根.
可见,式子b2-4ac决定了一元二次方程的根的情况.
当b2-4ac>0及b2-4ac=0时,一元二次方程ax2+bx+c=0(a≠0)的实数根可写为
的形式.
当b2-4ac≥0时,方程ax2+bx+c=0(a≠0)的实数根可写为
的形式,这个式子叫做一元二次方程ax2+bx+c=0(a≠0)的求根公式.
解一元二次方程时,把各系数直接代入求根公式,这种解一元二次方程的方法叫做公式法.
一元二次方程ax2+bx+c=0(a≠0)的解法
直接开平方法
配方法
公式法
例
用公式法解方程5x2-3x=x+1.
解:方程化为5x2-4x-1=0.
方程有两个不相等实数根
即:
巩固落实
(1)化
“一般形式”.
(2)确定a,b,c(注意符号).
(3)计算b2-4ac的值.
(4)当b2-4ac≥0时
,将a,b,c及b2-4ac代入公式
(5)结果化成最简形式.
用公式法解一元二次方程的一般步骤
当b2-4ac<0时
,方程无实数根.
公式法
解:
方程有两个不相等实数根
配方法
问题4
比较两种解法,能体会出为什么学习公式法吗?
①利用配方法可以推导出求根公式,配方是推
导求根公式的中间过程.
②公式法则省去了配方的中间过程,直接利用了配方的结果.
③公式法的优点是操作简单,直接计算,是解一元二次方程的通法.
课堂练习
1.一元二次方程x2-4x+5=0的根的情况是(
)
A.有两个不相等的实数根
B.有两个相等的实数根
C.只有一个实数根
D.没有实数根
D
课堂练习
2.已知A=a+2,B=a2-a+5,C=a2+5a+19.
(1)求证:B-A>0;
(2)指出A与C哪个大?并说明理由.
解:(1)B-A=(a-1)2+2>0
(2)C-A=(a+2)2+13>0,∴C>A
用公式法解一元二次方程的“四个步骤”:
(1)
把一元二次方程化为一般形式.
(2)
确定a,b,c的值.
(3)
计算b2-4ac的值.
(4)
当b2-4ac≥0时,把a,b,c的值代入求根公式,求出方程的两个实数根;
当b2-4ac<0时,方程无实数根.
课堂小结
用公式法解下列方程:
课后作业
同课章节目录
