1.1.2空间向量的数量积运算 课件 人教A版选择性必修第一册(共15张PPT)
文档属性
| 名称 | 1.1.2空间向量的数量积运算 课件 人教A版选择性必修第一册(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 334.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 21:37:59 | ||
图片预览






文档简介
(共15张PPT)
1.1.2
空间向量的数量积运算
复习
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
5、共线向量与共面向量
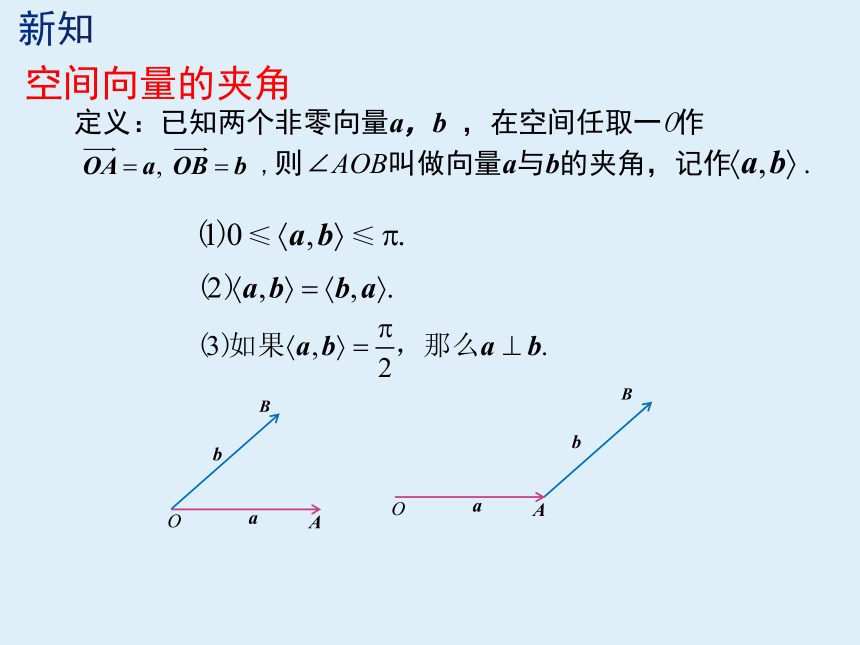
空间向量的夹角
定义:已知两个非零向量a,b
,在空间任取一O作
,则∠AOB叫做向量a与b的夹角,记作
.
O
A
a
B
b
O
A
a
B
b
新知
空间向量的数量积
(零向量与任意向量的数量积为0.)
?
空间向量数量积的性质
定义:已知两个非零向量a,b,则
叫做a,b的数量积,记作
,即
新知
空间向量数量积的运算律
阅读教材P7思考:
思考
1、对于三个均不为0的数a、b、c,若ab=ac,则b=c.对于向量a、b、c,由ab=ac,你能得到b=c吗?如若不能,请举出反例。
2、对于三个均不为0的数a、b、c,若ab=c,则
(或
)
.对于向量a、b,由a·b=k,能得到
(或
)
吗?
3、对于三个均不为0的数a、b、c,有(ab)c=a(bc),对于向量a、b、c,有(a·b)c=a(b·c)成立吗?为什么?
a
c
b
1、不成立
阅读教材P7思考:
思考
1、对于三个均不为0的数a、b、c,若ab=ac,则b=c.对于向量a、b、c,由ab=ac,你能得到b=c吗?如若不能,请举出反例。
2、对于三个均不为0的数a、b、c,若ab=c,则
(或
)
.对于向量a、b,由a·b=k,能得到
(或
)
吗?
3、对于三个均不为0的数a、b、c,有(ab)c=a(bc),对于向量a、b、c,有(a·b)c=a(b·c)成立吗?为什么?
不能得到
3、不成立
×
×
×
×
1
练习
D1
A
A1
D
C
B
C1
B1
如图,正方体ABCD-A1B1C1D1
的边长为1,求:
=0.
练习
B
A
D
C
解:
例题
练习
例3:已知直线m
,n是平面?内的两条相交直线,如果
l⊥m,
l⊥n,求证:
l⊥?
.
m
n
g
证明:在?内作不与m、n重合的任意一条直线g,分别在l、m、n、g上取非零向量l、m、n、g.因m与n相交,所以向量m、n不平行.
?
例题
∵
l·m=0
,
l·n=0
.
∴
l·g=0.
∴
l⊥g
.
∴直线
l⊥直线g.
∴直线
l⊥
?
.
由向量共面的充要条件可知,存在唯一的有序实数对(x,y),使
g=xm+yn,
l·g=xl·m+yl·n.
a
a
b
c
α
a
a
l
c
α
思考
a
β
a
A1
B
A
B1
课堂小结
1、空间两个向量的夹角
2、空间向量数量积的定义及几何意义
3、空间数量积的性质
4、空间向量数量积的运算律
作业:
课本P8
练习1、3
1.1.2
空间向量的数量积运算
复习
1、空间向量的定义及表示方法
2、特殊的向量
3、向量的加减法
4、向量的数乘运算
5、共线向量与共面向量
空间向量的夹角
定义:已知两个非零向量a,b
,在空间任取一O作
,则∠AOB叫做向量a与b的夹角,记作
.
O
A
a
B
b
O
A
a
B
b
新知
空间向量的数量积
(零向量与任意向量的数量积为0.)
?
空间向量数量积的性质
定义:已知两个非零向量a,b,则
叫做a,b的数量积,记作
,即
新知
空间向量数量积的运算律
阅读教材P7思考:
思考
1、对于三个均不为0的数a、b、c,若ab=ac,则b=c.对于向量a、b、c,由ab=ac,你能得到b=c吗?如若不能,请举出反例。
2、对于三个均不为0的数a、b、c,若ab=c,则
(或
)
.对于向量a、b,由a·b=k,能得到
(或
)
吗?
3、对于三个均不为0的数a、b、c,有(ab)c=a(bc),对于向量a、b、c,有(a·b)c=a(b·c)成立吗?为什么?
a
c
b
1、不成立
阅读教材P7思考:
思考
1、对于三个均不为0的数a、b、c,若ab=ac,则b=c.对于向量a、b、c,由ab=ac,你能得到b=c吗?如若不能,请举出反例。
2、对于三个均不为0的数a、b、c,若ab=c,则
(或
)
.对于向量a、b,由a·b=k,能得到
(或
)
吗?
3、对于三个均不为0的数a、b、c,有(ab)c=a(bc),对于向量a、b、c,有(a·b)c=a(b·c)成立吗?为什么?
不能得到
3、不成立
×
×
×
×
1
练习
D1
A
A1
D
C
B
C1
B1
如图,正方体ABCD-A1B1C1D1
的边长为1,求:
=0.
练习
B
A
D
C
解:
例题
练习
例3:已知直线m
,n是平面?内的两条相交直线,如果
l⊥m,
l⊥n,求证:
l⊥?
.
m
n
g
证明:在?内作不与m、n重合的任意一条直线g,分别在l、m、n、g上取非零向量l、m、n、g.因m与n相交,所以向量m、n不平行.
?
例题
∵
l·m=0
,
l·n=0
.
∴
l·g=0.
∴
l⊥g
.
∴直线
l⊥直线g.
∴直线
l⊥
?
.
由向量共面的充要条件可知,存在唯一的有序实数对(x,y),使
g=xm+yn,
l·g=xl·m+yl·n.
a
a
b
c
α
a
a
l
c
α
思考
a
β
a
A1
B
A
B1
课堂小结
1、空间两个向量的夹角
2、空间向量数量积的定义及几何意义
3、空间数量积的性质
4、空间向量数量积的运算律
作业:
课本P8
练习1、3
