2021-2022学年冀教新版九年级上册数学《第23章 数据分析》单元测试卷(word版有答案)
文档属性
| 名称 | 2021-2022学年冀教新版九年级上册数学《第23章 数据分析》单元测试卷(word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 180.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 08:15:27 | ||
图片预览




文档简介
2021-2022学年冀教新版九年级上册数学《第23章
数据分析》单元测试卷(有答案)
一.选择题
1.为了了解某校九年级300名学生的体重情况,从中抽取50名学生的体重进行分析,在这项调查中,样本是指( )
A.300名学生
B.300名学生的体重
C.被抽取的50名学生
D.被抽取的50名学生的体重
2.在一次中学生田径运动会上,参加跳远的15名运动员的成绩如下表所示
成绩(米)
4.50
4.60
4.65
4.70
4.75
4.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别是( )
A.4.65、4.70
B.4.65、4.75
C.4.70、4.75
D.4.70、4.70
3.甲、乙、丙、丁四名选手参加体育训练,近期10次跳绳测试的平均成绩都是每分钟175下,其方差如下表:
选手
甲
乙
丙
丁
方差s2
0.021
0.020
0.022
0.018
则这次跳绳中,这四个人发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
4.某工厂生产质量为1克,5克,10克,25克四种规格的球,现从中取x个球装到一个空箱子里,这时箱子里球的平均质量为20克,若再放入一个25克的球,则箱子里球的平均质量变为21克,则x的值为( )
A.3
B.4
C.5
D.6
5.下表是某校12名男子足球队队员的年龄分布:
年龄(岁)
13
14
15
16
频数
1
2
5
4
该校男子足球队队员的平均年龄为( )岁
A.13
B.14
C.15
D.16
6.在一次田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m)
1.50
1.55
1.60
1.65
1.70
1.75
1.80
人数
1
1
1
4
3
3
2
这些运动员跳高成绩的中位数是( )
A.1.65
B.1.70
C.4
D.3
7.小明抽样调查了某校30位男生的衬衫尺码,数据如下(单位:cm)
领口大小
37
38
39
40
41
人数
6
7
6
6
5
这组数据的中位数是( )
A.37
B.38
C.39
D.40
8.数学兴趣小组的甲、乙、丙、丁四位同学进行还原魔方练习,下表记录了他们10次还原魔方所用时间的平均值与方差S2:
甲
乙
丙
丁
(秒)
30
30
28
28
S2
1.21
1.05
1.21
1.05
要从中选择一名还原魔方用时少又发挥稳定的同学参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
9.我校七年级举行大合唱比赛,六位评委给七年级一班的打分如下:(单位:分)9.2,9.4,9.6,9.5,9.8,9.5,则该班得分的平均分为( )
A.9.45分
B.9.50
分
C.9.55
分
D.9.60分
10.某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A.2.5
B.2
C.1
D.﹣2
二.填空题
11.为了解被拆迁的1680户家庭对拆迁补偿方案是否满意,市主管部门调查了其中的80户家庭,有66户对方案表示满意,14户表示不满意,在这一抽样调查中,样本容量是
.
12.若1、2、x、5、7五个数的平均数为4,则x的值是
.
13.学校以德、智、体三项成绩来计算学生的平均成绩,三项成绩的比例依次为1:3:1,李明三项成绩分别为90分,95分,96分,则李明的平均成绩为
分.
14.甲,乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差S2甲与S2乙的大小关系是S2甲
S2乙.(填“>”或“<”)
15.已知一组数据:86,85,82,97,73,这组数据的中位数是
.
16.已知一组数据5,4,x,3,9的平均数为5,则x的值是
.
17.数据2,4,6,x,3,9的众数为3,则这组数据的中位数为
.
18.选作题(要求在①、②中任选一题作答,若多选,则按第①题计分)
①如图,AB∥CD,EF⊥DB,垂足为点E,∠1=50°,则∠2的度数是
;
②用计算器求一组数据71,75,63,89,100,77,86的平均数为
(精确到0.1).
19.某店最近一周,每天销售某种礼物的个数为:12,10,11,14,11,13,16.这组数据的中位数是
.
20.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是
.
三.解答题
21.时代中学七年级共10个班,为了了解本年级学生一周中收看电视节目所用的时间,小亮利用放学时在校门口调查了他认识的60名七年级同学.
(1)小亮的调查是抽样调查吗?
(2)如果是抽样调查,指出调查的总体、个体和样本容量;
(3)根据他调查的结果,能反映七年级同学平均一周收看电视的时间吗?
22.某校某年级共有800名学生,为了解在一次数学测试中学生的成绩,随机抽取了20名学生的考试成绩,整理后得到下表.
成绩
45
55
65
75
85
95
人数
2
2
3
4
5
4
(1)试计算所抽取的20名学生的数学成绩的平均数;
(2)根据抽样情况,试估计该年级共有多少名学生在这次数学测验中成绩及格?(60分以上为及格)
23.已知小红的成绩如下表:
文化成绩
综合素质成绩
总成绩
测验1
测验2
测验3
小红
560分
580分
630分
12
(1)小红的这三次文化测试成绩的平均分是
分;
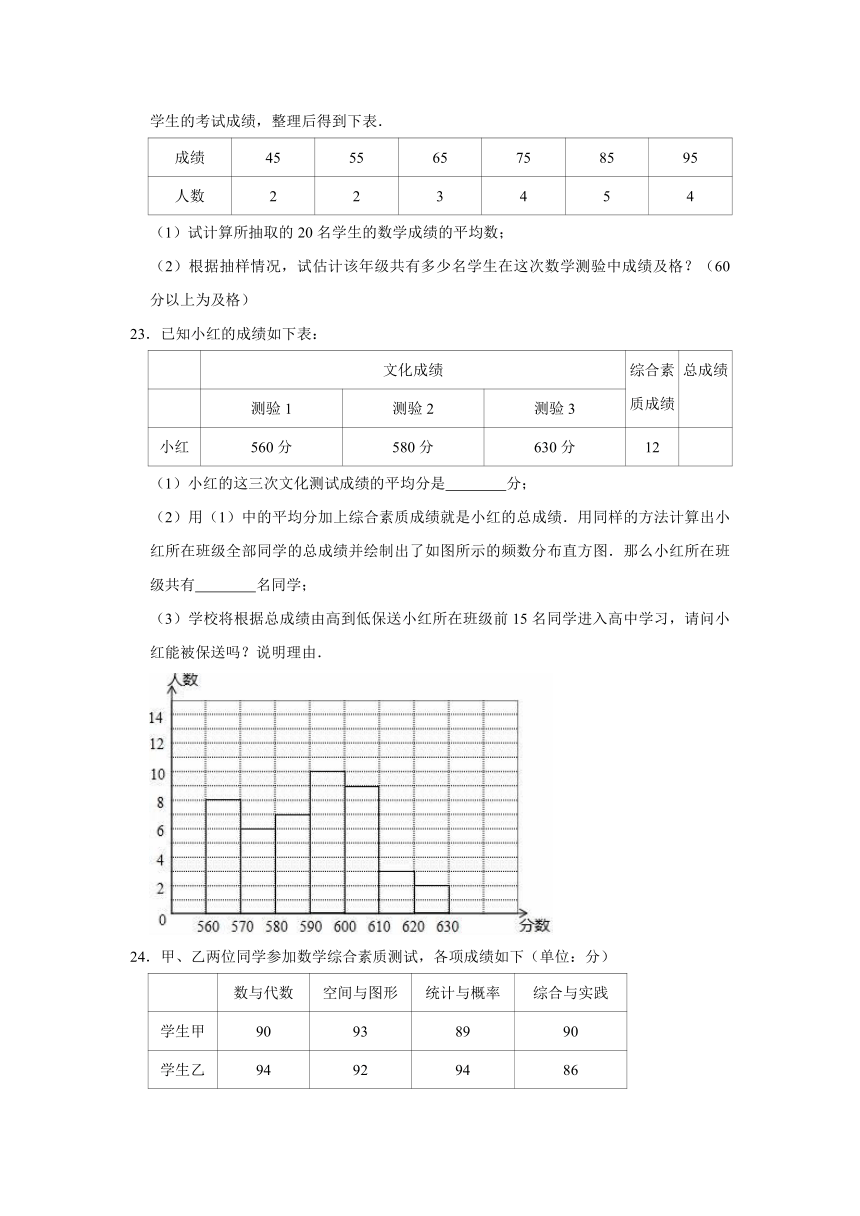
(2)用(1)中的平均分加上综合素质成绩就是小红的总成绩.用同样的方法计算出小红所在班级全部同学的总成绩并绘制出了如图所示的频数分布直方图.那么小红所在班级共有
名同学;
(3)学校将根据总成绩由高到低保送小红所在班级前15名同学进入高中学习,请问小红能被保送吗?说明理由.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
25.在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140
146
143
175
125
164
134
155
152
168
162
148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据中位数,推断他的成绩如何?
26.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲
85
88
84
85
83
乙
83
87
84
86
85
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
参考答案与试题解析
一.选择题
1.解:为了了解某校九年级300名学生的体重情况,从中抽取50名学生的体重进行分析,在这项调查中,样本是指被抽取的50名学生的体重.
故选:D.
2.解:把分数从低到高排列,第八个人把总人数分为左右相等的两部分,第八个人对应的分数是4.70,所以中位数是4.70;分数4.75出现最多为4次,所以众数是4.75.
故选:C.
3.解:因为0.018<0.020<0.021<0.022,
所以丁发挥最稳定.
故选:D.
4.解:根据题意,得:=21,
解得x=4,
经检验:x=4是原分式方程的解,
故选:B.
5.解:该校男子足球队队员的平均年龄为=15(岁),
故选:C.
6.解:由表格中的数据可知,成绩按照从小到大排列的第8个数据是1.70,
故这些运动员跳高成绩的中位数是1.70,
故选:B.
7.解:∵共有30个数据,其中位数是第15、16个数据的平均数,且第15、16个数据均为39,
∴这组数据的中位数为39,
故选:C.
8.解:因为乙和丁的方差最小,但丁平均数最小,
所以丁还原魔方用时少又发挥稳定.
故选:D.
9.解:(9.2+9.4+9.6+9.5+9.8+9.5)÷6=9.50(分).
故该班得分的平均分为9.50分.
故选:B.
10.解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是﹣=﹣2;
故选:D.
二.填空题
11.解:在这一抽样调查中,样本容量是80,
故答案为:80.
12.解:由题意得,=4,
解得:x=5.
故答案为:5.
13.解:根据题意得:
(90×1+95×3+96×1)÷(1+3+1)=94.2(分),
答:李明的平均成绩为94.2分.
故答案为:94.2.
14.解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差S2甲>S2乙.
故答案为>.
15.解:将数据86,85,82,97,73按照从小到大排列是:73,82,85,86,97,
故这组数据的中位数是85,
故答案为:85.
16.解:∵5,4,x,3,9的平均数为5,
∴(5+4+x+3+9)÷5=5,
解得:x=4,
则x的值是4;
故答案为:4.
17.解:∵数据2,4,6,x,3,9的众数为3,
∴x=3,
则这组数据为2、3、3、4、6、9,
所以这组数据的中位数为=3.5,
故答案为:3.5.
18.解:①∵EF⊥DB,
∴∠FED=90°,
∴∠1+∠D=90°,
∵∠1=50°,
∴∠D=40°,
∵AB∥CD,
∴∠2=∠D=40°,
故答案为:40°.
②≈80.1,
故答案为:80.1.
19.解:首先对这组7个数据12,10,11,14,11,13,16按从小到大的顺序排列为:10,11,11,12,13,14,16,
排在最中间的数据为12,
故这组数据的中位数为12,
故答案为:12.
20.解:∵数据8,6,x,4,7的平均数是6,
∴=6,
解得:x=5,
这组数据的方差是S2=×[(8﹣6)2+(6﹣6)2+(5﹣6)2+(4﹣6)2+(7﹣6)2]=2,
故答案为:2.
三.解答题
21.解:(1)小亮的调查是抽样调查;
(2)调查的总体是时代中学七年级共10个班一周中收看电视节目所用的时间;
个体是每个同学一周中收看电视节目所用的时间;
样本容量是60.
(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面(答案不唯一,合理即可).
22.解:(1)由题意可得,
=75(分),
即所抽取的20名学生的数学成绩的平均数是75分;
(2)800×=640(名),
即估计该年级共有640名学生在这次数学测验中成绩及格.
23.解:(1)由题意可知:小红的这三次文化测试成绩的平均分是=590;
(2)由频数分布直方图可以看出:小红所在班级共有8+6+7+10+9+3+2=45(人);
(3)小红的总成绩为590+12=602分,600分以上的学生共有9+3+2=14(人),
∵14<15,
∴小红能被保送.
24.解:(1)甲的成绩从小到大的顺序排列为:89,90,90,93,中位数为90;
乙的成绩从小到大的顺序排列为:86,92,94,94,中位数为(92+94)÷2=93.
答:甲成绩的中位数是90,乙成绩的中位数是93;
(2)3+3+2+2=10
甲90×+93×+89×+90×
=27+27.9+17.8+18
=90.7(分)
乙94×+92×+94×+86×
=28.2+27.6+18.8+17.2
=91.8(分)
答:甲的数学综合素质成绩为90.7分,乙的数学综合素质成绩为91.8分.
25.解:(1)将这组数据按照从小到大的顺序排列为:125,134,140,143,146,148,152,155,162,164,168,175,
则中位数为:=150,
平均数为:=151;
(2)由(1)可得,中位数为150,可以估计在这次马拉松比赛中,大约有一半选手的成绩快于150分钟,有一半选手的成绩慢于150分钟,这名选手的成绩为147分钟,快于中位数150分钟,可以推断他的成绩估计比一半以上选手的成绩好.
26.解:(1)甲平均数:×(85+88+84+85+83)=×425=85,
乙平均数:×(83+87+84+86+85)=×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
=×(0+9+1+0+4),
=2.8,
S乙2=×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
=×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.
数据分析》单元测试卷(有答案)
一.选择题
1.为了了解某校九年级300名学生的体重情况,从中抽取50名学生的体重进行分析,在这项调查中,样本是指( )
A.300名学生
B.300名学生的体重
C.被抽取的50名学生
D.被抽取的50名学生的体重
2.在一次中学生田径运动会上,参加跳远的15名运动员的成绩如下表所示
成绩(米)
4.50
4.60
4.65
4.70
4.75
4.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别是( )
A.4.65、4.70
B.4.65、4.75
C.4.70、4.75
D.4.70、4.70
3.甲、乙、丙、丁四名选手参加体育训练,近期10次跳绳测试的平均成绩都是每分钟175下,其方差如下表:
选手
甲
乙
丙
丁
方差s2
0.021
0.020
0.022
0.018
则这次跳绳中,这四个人发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
4.某工厂生产质量为1克,5克,10克,25克四种规格的球,现从中取x个球装到一个空箱子里,这时箱子里球的平均质量为20克,若再放入一个25克的球,则箱子里球的平均质量变为21克,则x的值为( )
A.3
B.4
C.5
D.6
5.下表是某校12名男子足球队队员的年龄分布:
年龄(岁)
13
14
15
16
频数
1
2
5
4
该校男子足球队队员的平均年龄为( )岁
A.13
B.14
C.15
D.16
6.在一次田径运动会上,参加男子跳高的15名运动员的成绩如表所示:
成绩(m)
1.50
1.55
1.60
1.65
1.70
1.75
1.80
人数
1
1
1
4
3
3
2
这些运动员跳高成绩的中位数是( )
A.1.65
B.1.70
C.4
D.3
7.小明抽样调查了某校30位男生的衬衫尺码,数据如下(单位:cm)
领口大小
37
38
39
40
41
人数
6
7
6
6
5
这组数据的中位数是( )
A.37
B.38
C.39
D.40
8.数学兴趣小组的甲、乙、丙、丁四位同学进行还原魔方练习,下表记录了他们10次还原魔方所用时间的平均值与方差S2:
甲
乙
丙
丁
(秒)
30
30
28
28
S2
1.21
1.05
1.21
1.05
要从中选择一名还原魔方用时少又发挥稳定的同学参加比赛,应该选择( )
A.甲
B.乙
C.丙
D.丁
9.我校七年级举行大合唱比赛,六位评委给七年级一班的打分如下:(单位:分)9.2,9.4,9.6,9.5,9.8,9.5,则该班得分的平均分为( )
A.9.45分
B.9.50
分
C.9.55
分
D.9.60分
10.某同学使用计算器求30个数据的平均数时,错将其中一个数据75输入为15,那么所求出的平均数与实际平均数的差是( )
A.2.5
B.2
C.1
D.﹣2
二.填空题
11.为了解被拆迁的1680户家庭对拆迁补偿方案是否满意,市主管部门调查了其中的80户家庭,有66户对方案表示满意,14户表示不满意,在这一抽样调查中,样本容量是
.
12.若1、2、x、5、7五个数的平均数为4,则x的值是
.
13.学校以德、智、体三项成绩来计算学生的平均成绩,三项成绩的比例依次为1:3:1,李明三项成绩分别为90分,95分,96分,则李明的平均成绩为
分.
14.甲,乙两地7月上旬的日平均气温如图所示,则甲,乙两地这10天中日平均气温的方差S2甲与S2乙的大小关系是S2甲
S2乙.(填“>”或“<”)
15.已知一组数据:86,85,82,97,73,这组数据的中位数是
.
16.已知一组数据5,4,x,3,9的平均数为5,则x的值是
.
17.数据2,4,6,x,3,9的众数为3,则这组数据的中位数为
.
18.选作题(要求在①、②中任选一题作答,若多选,则按第①题计分)
①如图,AB∥CD,EF⊥DB,垂足为点E,∠1=50°,则∠2的度数是
;
②用计算器求一组数据71,75,63,89,100,77,86的平均数为
(精确到0.1).
19.某店最近一周,每天销售某种礼物的个数为:12,10,11,14,11,13,16.这组数据的中位数是
.
20.若一组数据8,6,x,4,7的平均数是6,则这组数据的方差是
.
三.解答题
21.时代中学七年级共10个班,为了了解本年级学生一周中收看电视节目所用的时间,小亮利用放学时在校门口调查了他认识的60名七年级同学.
(1)小亮的调查是抽样调查吗?
(2)如果是抽样调查,指出调查的总体、个体和样本容量;
(3)根据他调查的结果,能反映七年级同学平均一周收看电视的时间吗?
22.某校某年级共有800名学生,为了解在一次数学测试中学生的成绩,随机抽取了20名学生的考试成绩,整理后得到下表.
成绩
45
55
65
75
85
95
人数
2
2
3
4
5
4
(1)试计算所抽取的20名学生的数学成绩的平均数;
(2)根据抽样情况,试估计该年级共有多少名学生在这次数学测验中成绩及格?(60分以上为及格)
23.已知小红的成绩如下表:
文化成绩
综合素质成绩
总成绩
测验1
测验2
测验3
小红
560分
580分
630分
12
(1)小红的这三次文化测试成绩的平均分是
分;
(2)用(1)中的平均分加上综合素质成绩就是小红的总成绩.用同样的方法计算出小红所在班级全部同学的总成绩并绘制出了如图所示的频数分布直方图.那么小红所在班级共有
名同学;
(3)学校将根据总成绩由高到低保送小红所在班级前15名同学进入高中学习,请问小红能被保送吗?说明理由.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数
空间与图形
统计与概率
综合与实践
学生甲
90
93
89
90
学生乙
94
92
94
86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
25.在一次男子马拉松长跑比赛中,随机抽得12名选手所用的时间(单位:分钟)得到如下样本数据:140
146
143
175
125
164
134
155
152
168
162
148
(1)计算该样本数据的中位数和平均数;
(2)如果一名选手的成绩是147分钟,请你依据样本数据中位数,推断他的成绩如何?
26.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲
85
88
84
85
83
乙
83
87
84
86
85
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
参考答案与试题解析
一.选择题
1.解:为了了解某校九年级300名学生的体重情况,从中抽取50名学生的体重进行分析,在这项调查中,样本是指被抽取的50名学生的体重.
故选:D.
2.解:把分数从低到高排列,第八个人把总人数分为左右相等的两部分,第八个人对应的分数是4.70,所以中位数是4.70;分数4.75出现最多为4次,所以众数是4.75.
故选:C.
3.解:因为0.018<0.020<0.021<0.022,
所以丁发挥最稳定.
故选:D.
4.解:根据题意,得:=21,
解得x=4,
经检验:x=4是原分式方程的解,
故选:B.
5.解:该校男子足球队队员的平均年龄为=15(岁),
故选:C.
6.解:由表格中的数据可知,成绩按照从小到大排列的第8个数据是1.70,
故这些运动员跳高成绩的中位数是1.70,
故选:B.
7.解:∵共有30个数据,其中位数是第15、16个数据的平均数,且第15、16个数据均为39,
∴这组数据的中位数为39,
故选:C.
8.解:因为乙和丁的方差最小,但丁平均数最小,
所以丁还原魔方用时少又发挥稳定.
故选:D.
9.解:(9.2+9.4+9.6+9.5+9.8+9.5)÷6=9.50(分).
故该班得分的平均分为9.50分.
故选:B.
10.解:求30个数据的平均数时,错将其中一个数据75输入为15,即使总和减少了60,
那么由此求出的这组数据的平均数与实际平均数的差是﹣=﹣2;
故选:D.
二.填空题
11.解:在这一抽样调查中,样本容量是80,
故答案为:80.
12.解:由题意得,=4,
解得:x=5.
故答案为:5.
13.解:根据题意得:
(90×1+95×3+96×1)÷(1+3+1)=94.2(分),
答:李明的平均成绩为94.2分.
故答案为:94.2.
14.解:∵甲地日平均气温的比乙地的日平均气温的变化幅度大,
∴方差S2甲>S2乙.
故答案为>.
15.解:将数据86,85,82,97,73按照从小到大排列是:73,82,85,86,97,
故这组数据的中位数是85,
故答案为:85.
16.解:∵5,4,x,3,9的平均数为5,
∴(5+4+x+3+9)÷5=5,
解得:x=4,
则x的值是4;
故答案为:4.
17.解:∵数据2,4,6,x,3,9的众数为3,
∴x=3,
则这组数据为2、3、3、4、6、9,
所以这组数据的中位数为=3.5,
故答案为:3.5.
18.解:①∵EF⊥DB,
∴∠FED=90°,
∴∠1+∠D=90°,
∵∠1=50°,
∴∠D=40°,
∵AB∥CD,
∴∠2=∠D=40°,
故答案为:40°.
②≈80.1,
故答案为:80.1.
19.解:首先对这组7个数据12,10,11,14,11,13,16按从小到大的顺序排列为:10,11,11,12,13,14,16,
排在最中间的数据为12,
故这组数据的中位数为12,
故答案为:12.
20.解:∵数据8,6,x,4,7的平均数是6,
∴=6,
解得:x=5,
这组数据的方差是S2=×[(8﹣6)2+(6﹣6)2+(5﹣6)2+(4﹣6)2+(7﹣6)2]=2,
故答案为:2.
三.解答题
21.解:(1)小亮的调查是抽样调查;
(2)调查的总体是时代中学七年级共10个班一周中收看电视节目所用的时间;
个体是每个同学一周中收看电视节目所用的时间;
样本容量是60.
(3)这个调查的结果不能反映七年级同学平均一周收看电视的时间,因为抽样太片面(答案不唯一,合理即可).
22.解:(1)由题意可得,
=75(分),
即所抽取的20名学生的数学成绩的平均数是75分;
(2)800×=640(名),
即估计该年级共有640名学生在这次数学测验中成绩及格.
23.解:(1)由题意可知:小红的这三次文化测试成绩的平均分是=590;
(2)由频数分布直方图可以看出:小红所在班级共有8+6+7+10+9+3+2=45(人);
(3)小红的总成绩为590+12=602分,600分以上的学生共有9+3+2=14(人),
∵14<15,
∴小红能被保送.
24.解:(1)甲的成绩从小到大的顺序排列为:89,90,90,93,中位数为90;
乙的成绩从小到大的顺序排列为:86,92,94,94,中位数为(92+94)÷2=93.
答:甲成绩的中位数是90,乙成绩的中位数是93;
(2)3+3+2+2=10
甲90×+93×+89×+90×
=27+27.9+17.8+18
=90.7(分)
乙94×+92×+94×+86×
=28.2+27.6+18.8+17.2
=91.8(分)
答:甲的数学综合素质成绩为90.7分,乙的数学综合素质成绩为91.8分.
25.解:(1)将这组数据按照从小到大的顺序排列为:125,134,140,143,146,148,152,155,162,164,168,175,
则中位数为:=150,
平均数为:=151;
(2)由(1)可得,中位数为150,可以估计在这次马拉松比赛中,大约有一半选手的成绩快于150分钟,有一半选手的成绩慢于150分钟,这名选手的成绩为147分钟,快于中位数150分钟,可以推断他的成绩估计比一半以上选手的成绩好.
26.解:(1)甲平均数:×(85+88+84+85+83)=×425=85,
乙平均数:×(83+87+84+86+85)=×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
=×(0+9+1+0+4),
=2.8,
S乙2=×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
=×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
