12.2 三角形全等的判定同步练习 2020-2021学年 人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 12.2 三角形全等的判定同步练习 2020-2021学年 人教版八年级数学上册(Word版 含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 478.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 00:00:00 | ||
图片预览


文档简介
12.2
三角形全等的判定(第四课时)
一、选择题
1.在下列条件中,一定不能保证两直角三角形全等的是( )
A.两直角边对应相等
B.一直角边与一锐角对应相等
C.两锐角对应相等
D.斜边与一锐角对应相等
2.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS
B.SAS
C.ASA
D.AAS
3.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
4.一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
A.不能
B.带①
C.带②
D.带③
5.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=8
D.∠C=90°,AB=6
6.下列各组条件中,能判断两个直角三角形全等的是( )
A.一组边对应相等
B.两组直角边对应相等
C.两组锐角对应相等
D.一组锐角对应相等
7.如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
A.5对
B.4对
C.3对
D.2对
8.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块
B.第2块
C.第3块
D.第4块
10.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题
11.如图所示,在△ABC中,AD⊥BC,请你添加一个条件,写出一个正确结论(不在图中添加辅助线),条件是
,结论是
.
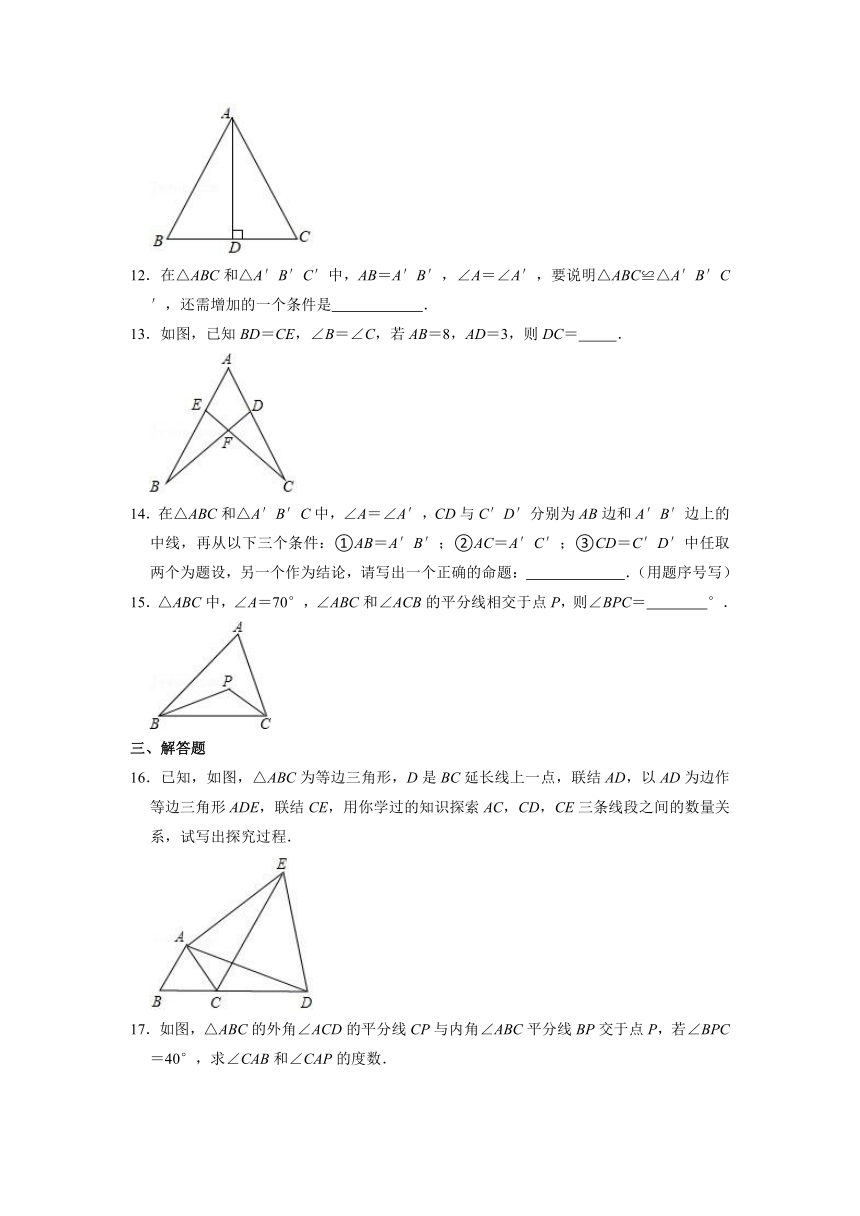
12.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需增加的一个条件是
.
13.如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC=
.
14.在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题:
.(用题序号写)
15.△ABC中,∠A=70°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=
°.
三、解答题
16.已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
17.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
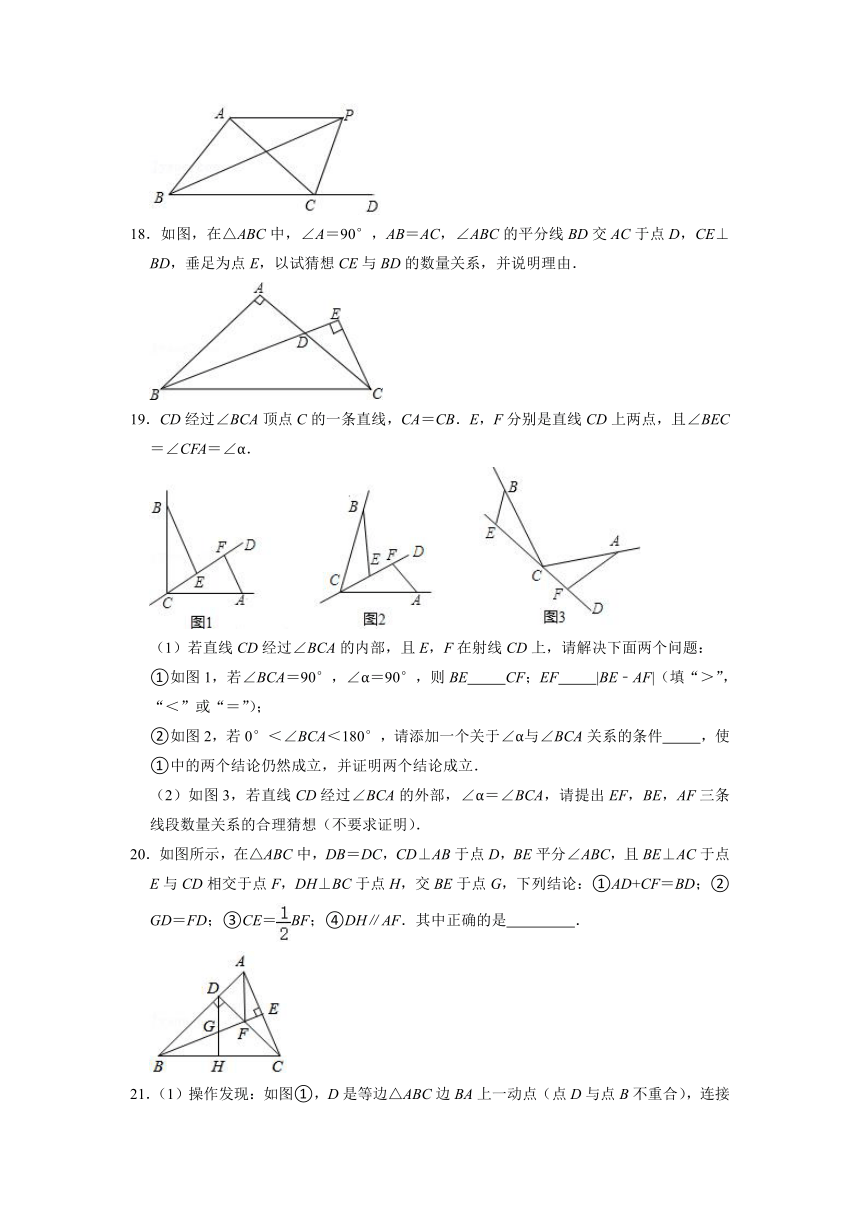
18.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
19.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
20.如图所示,在△ABC中,DB=DC,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E与CD相交于点F,DH⊥BC于点H,交BE于点G,下列结论:①AD+CF=BD;②GD=FD;③CE=BF;④DH∥AF.其中正确的是
.
21.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
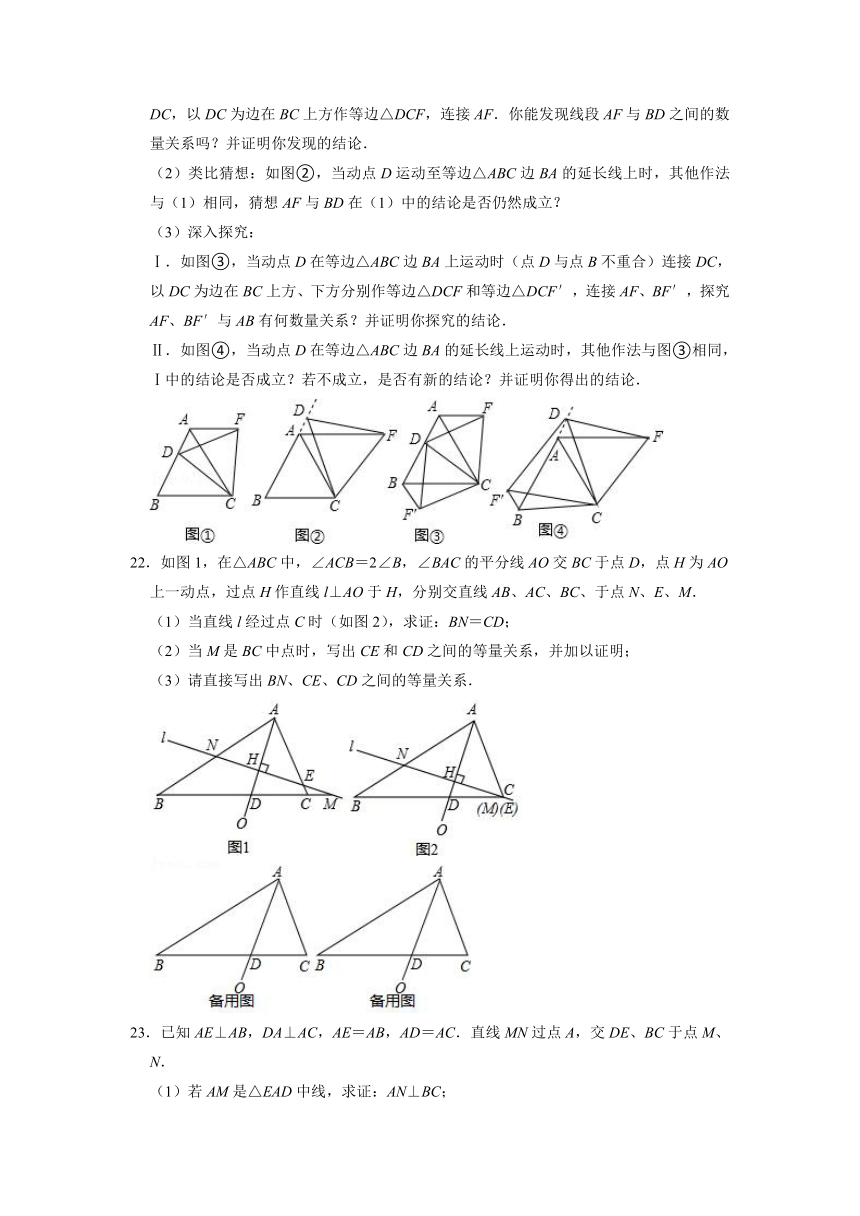
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△ABC边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
22.如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.
23.已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
参考答案与试题解析
一、选择题
1.在下列条件中,一定不能保证两直角三角形全等的是( )
A.两直角边对应相等
B.一直角边与一锐角对应相等
C.两锐角对应相等
D.斜边与一锐角对应相等
【分析】根据三角形全等的判定方法,利用直角三角形隐含的直角相等的条件,对各选项分析判断后利用排除法求解.
【解答】解:A、两直角边对应相等可以利用“SAS”证明两三角形全等,故本选项不符合题意;
B、一直角边与一锐角对应相等,可以利用“AAS”证明两三角形全等,故本选项不符合题意;
C、两锐角对应相等,不能保证两直角三角形全等,故本选项符合题意;
D、斜边与一锐角对应相等,可以利用“AAS”证明两三角形全等,故本选项不符合题意.
故选:C.
2.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS
B.SAS
C.ASA
D.AAS
【分析】根据全等三角形的判定进行判断,注意看题目中提供了哪些证明全等的要素,要根据已知选择判断方法.
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
3.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
【分析】根据作一个角等于已知角的作法即可得出结论.
【解答】解:先以点A为圆心,以任意长为半径画弧,分别交AC,AB于点Q,P;
再以点E为圆心,AQ的长为半径画弧,交AC于点G,
再以点G为圆心,PQ的长为半径画弧.
故选:D.
4.一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
A.不能
B.带①
C.带②
D.带③
【分析】根据全等三角形的判定方法结合图形判断出带③去.
【解答】解:由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选:D.
5.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=8
D.∠C=90°,AB=6
【分析】看是否符合所学的全等的公理或定理及三角形三边关系即可.
【解答】解:A、符合全等三角形的ASA,能作出唯一三角形;
B、属于全等三角形判定中的SSA情况,不能作出唯一三角形;
C不符合三角形三边之间的关系,不能作出三角形;
D只有两个条件,不能作出唯一三角形.
故选:A.
6.下列各组条件中,能判断两个直角三角形全等的是( )
A.一组边对应相等
B.两组直角边对应相等
C.两组锐角对应相等
D.一组锐角对应相等
【分析】根据直角三角形全等的判定方法:HL、SAS、AAS、ASA分别进行分析即可.
【解答】解:A、一组边对应相等,不能判定两个直角三角形全等,故此选项错误;
B、两组直角边对应相等,可利用SAS判定两个直角三角形全等,故此选项正确;
C、两组锐角对应相等,不能判定两个直角三角形全等,故此选项错误;
D、一组锐角对应相等,不能判定两个直角三角形全等,故此选项错误;
故选:B.
7.如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
A.5对
B.4对
C.3对
D.2对
【分析】根据已知及全等三角形的判定方法进行分析,从而得到答案.
【解答】解:
∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共有4对.
故选:B.
8.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
【分析】此题是一道开放性题,实则还是考查学生对三角形全等的判定方法的掌握情况.此处可以运用排除法进行分析.
【解答】解:两个三角形有两个角对应相等,那么第三个角也相等,这两个三角形的关系是全等或相似.所以排除A、B、C;
D、如果一对等角的角平分线相等,两三角形全等,符合AAS,可证三角形全等.
故选:D.
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块
B.第2块
C.第3块
D.第4块
【分析】本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
【解答】解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:B.
10.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
【分析】锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,根据以上内容即可判断①;举出反例a=2,b=c=1,满足a+b>c,但是边长为1、1、2不能组成三角形,即可判断②;设三角形的三角为3x°,2x°,x°,由三角形的内角和定理得:3x+2x+x=180,求出3x=90,得出三角形是直角三角形,即可判断③;根据有两个角和一条边对应相等的两个三角形全等即可判断④.
【解答】解:∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;
∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;
∵设三角形的三角为3x°,2x°,x°,
∴由三角形的内角和定理得:3x+2x+x=180,
∴x=30,
3x=90,即三角形是直角三角形,∴③正确;
∵有两个角和一条边对应相等的两个三角形全等,∴④正确;
故选:C.
二、填空题
11.如图所示,在△ABC中,AD⊥BC,请你添加一个条件,写出一个正确结论(不在图中添加辅助线),条件是 AB=AC ,结论是 BD=CD .
【分析】这是一道开放性的题,只要添加一个条件并结合已知能证得结论即可.
【解答】解:∵AD⊥BC,AB=AC,
∴AD是△ABC的中线,
∴BD=CD.
故答案为:AB=AC,BD=CD.
12.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需增加的一个条件是 AC=A′C′ .
【分析】本题是开放题,已知AB=A′B′,∠A=∠A′,具备了一组边和一组角分别对应相等,故添加AC=A′C′,根据SAS判定△ABC≌△A′B′C′.此题答案不唯一.
【解答】解:所添条件为:AC=A′C′.
∵AB=A′B′,∠A=∠A′,AC=A′C′
∴△ABC≌△A′B′C′(SAS).
故填AC=A′C′.
13.如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC= 5 .
【分析】先根据“AAS”证明△ABD≌△ACE,则AB=AC=8,然后计算AC﹣AD即可.
【解答】解:在△ABD和△ACE中
,
∴△ABD≌△ACE,
∴AB=AC=8,
∴CD=AC﹣AD=8﹣3=5.
故答案为5.
14.在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题: 如果①②,那么③ .(用题序号写)
【分析】根据全等三角形的判定和性质进行解答.
【解答】解:∵在△ABC和△A′B′C中,∠A=∠A′,AB=A′B′,AC=A′C′,
∴△ABC≌△A′B′C,
∴CD=C′D′.
故如果①②那么③.
15.△ABC中,∠A=70°,∠ABC和∠ACB的平分线相交于点P,则∠BPC= 125 °.
【分析】根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵∠A=70,
∴∠ABC+∠ACB=180°﹣70°=110°,
∵∠ABC和∠ACB的平分线交于P,
∴∠PBC=∠ABC,∠PCB=ACB,
∴∠BPC=180°﹣(∠ABC+ACB)=125°,
故答案为:125.
三、解答题
16.已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
【分析】易证AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,即可求得∠BAD=∠CAE,即可证明△ABD≌△ACE,可得BD=CE,即可解题.
【解答】证明:∵△ABC和△ADE均是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE,(SAS)
∴BD=CE,
∴CA+CD=CE.
17.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠BAC+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=∠ACD,∠PBC=ABC,然后整理得到∠PCD=40°+∠ABC,再代入数据计算即可得解.
【解答】解:在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,
∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=∠ACD,∠PBC=∠ABC,
∴∠PCD=∠BPC+∠PBC=40°+∠ABC,
∴∠ACD=∠ABC+40°,
∴∠ACD﹣∠ABC=80°,
∴∠BAC=∠ACD﹣∠ABC=80°,
即∠CAB=80°.
∴∠CAP==50°.
18.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
【分析】延长BA、CE相交于点F,利用“角边角”证明△BCE和△BFE全等,根据全等三角形对应边相等可得CE=EF,根据等角的余角相等求出∠ABD=∠ACF,然后利用“角边角”证明△ABD和△ACF全等,根据全等三角形对应边相等可得BD=CF,然后求解即可.
【解答】解:BD=2CE.
理由如下:如图,延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,
在△ABD和△ACF中,,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE.
19.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE = CF;EF = |BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ∠α+∠BCA=180° ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
【分析】由题意推出∠CBE=∠ACF,再由AAS定理证△BCE≌△CAF,继而得答案.
【解答】解:(1)①∵∠BCA=90°,∠α=90°,
∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,
∴∠CBE=∠ACF,
∵CA=CB,∠BEC=∠CFA;
∴△BCE≌△CAF,
∴BE=CF;EF=|CF﹣CE|=|BE﹣AF|.
②所填的条件是:∠α+∠BCA=180°.
证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.
∵∠BCA=180°﹣∠α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF,
又∵BC=CA,∠BEC=∠CFA,
∴△BCE≌△CAF(AAS)
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=|BE﹣AF|.
(2)猜想:EF=BE+AF.
证明过程:
∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,
∴∠BCE=∠CAF,
又∵BC=CA,
∴△BCE≌△CAF(AAS).
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.
20.如图所示,在△ABC中,DB=DC,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E与CD相交于点F,DH⊥BC于点H,交BE于点G,下列结论:①AD+CF=BD;②GD=FD;③CE=BF;④DH∥AF.其中正确的是 ①②③④ .
【分析】通过证明△ABE≌△CBE,△ADC≌△FDB,可得AE=EC,BF=AC,AD=DF,利用等腰三角形的性质和直角三角形的性质依次判断可求解.
【解答】解:∵DB=DC,CD⊥AB,
∴∠DBC=∠DCB=45°,
∵BE平分∠ABC,
∴∠DBF=∠CBF=22.5°,
∵DH⊥BC,
∴∠DHB=∠BDC=90°,
∴∠BGH=67.5°=∠DFB,
∴∠DFB=∠DGF,
∴DG=DF,故②正确,
∵∠ABE=∠CBE,BE=BE,∠AEB=∠CEB,
∴△ABE≌△CBE(ASA),
∴AE=EC,
∵∠CAD+∠ACD=90°,∠CAD+∠ABE=90°,
∴∠ACD=∠ABE,
又∵BD=CD,∠BDF=∠CDA=90°,
∴△ADC≌△FDB(AAS),
∴BF=AC,AD=DF,
∴AD+CF=DF+CF=BD,故①正确;
∵AC=2CE,
∴CE=AC=BF,故③正确,
∵DB=DC,∠BDC=90°,DH⊥BC,
∴∠CDH=45°,
∵AD=DF,∠ADF=90°,
∴∠AFD=45°=∠CDH,
∴AF∥DH,故④正确,
故答案为:①②③④.
21.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△ABC边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
【分析】(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知AF=BD;
(2)通过证明△BCD≌△ACF,即可证明AF=BD;
(3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等);再结合(2)中的结论即可证得AF=AB+BF′.
【解答】解:(1)AF=BD;
证明如下:∵△ABC是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质);
同理知,DC=CF,∠DCF=60°;
∴∠BCA﹣∠DCA=∠DCF﹣∠DCA,即∠BCD=∠ACF;
在△BCD和△ACF中,
,
∴△BCD≌△ACF(SAS),
∴BD=AF(全等三角形的对应边相等);
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立;
(3)Ⅰ.AF+BF′=AB;
证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD(SAS),则BF′=AD,
∴AF+BF′=BD+AD=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;
证明如下:在△BCF′和△ACD中,
,
∴△BCF′≌△ACD(SAS),
∴BF′=AD(全等三角形的对应边相等);
又由(2)知,AF=BD;
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
22.如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.
【分析】(1)连接ND,先由已知条件证明DN=DC,再证明BN=DN即可;
(2)当M是BC中点时,CE和CD之间的等量关系为CD=2CE,过点C作CN'⊥AO交AB于N'.过点C作CG∥AB交直线l于G,再证明△BNM≌△CGM问题得证;
(3)BN、CE、CD之间的等量关系要分三种情况讨论:①当点M在线段BC上时;②当点M在BC的延长线上时;③当点M在CB的延长线上时;由(2)即可得出结论.
【解答】(1)证明:连接ND,如图2所示:
∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵直线l⊥AO于H,
∴∠AHN=∠AHE=90°,
∴∠ANH=∠AEH,
∴AN=AC,
∴NH=CH,
∴AH是线段NC的中垂线,
∴DN=DC,
∴∠DNH=∠DCH,
∴∠AND=∠ACB,
∵∠AND=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN,
∴BN=DC;
(2)解:当M是BC中点时,CE和CD之间的等量关系为CD=2CE,理由如下:
过点C作CN'⊥AO交AB于N',过点C作CG∥AB交直线l于点G,如图3所示:
由(1)得:BN'=CD,AN'=AC,AN=AE,
∴∠ANE=∠AEN,NN'=CE,
∴∠ANE=∠CGE,∠B=∠BCG,
∴∠CGE=∠AEN,
∴CG=CE,
∵M是BC中点,
∴BM=CM,
在△BNM和△CGM中,,
∴△BNM≌△CGM(ASA),
∴BN=CG,
∴BN=CE,
∴CD=BN'=NN'+BN=2CE;
(3)解:BN、CE、CD之间的等量关系:当点M在线段BC上时,CD=BN+CE;理由如下:
过点C作CN'⊥AO交AB于N',如图3所示:
由(2)得:NN'=CE,CD=BN'=BN+CE;
当点M在BC的延长线上时,CD=BN﹣CE;理由如下:
过点C作CN'⊥AO交AB于N',如图4所示:
同(2)得:NN'=CE,CD=BN'=BN﹣CE;
当点M在CB的延长线上时,CD=CE﹣BN;理由如下:
过点C作CN'⊥AO交AB于N',如图5所示:
同(2)得:NN'=CE,CD=BN'=CE﹣BN.
23.已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
【分析】(1)延长AM至F,使MF=AM,然后利用“边角边”证明△EMF和△DMA全等,根据全等三角形对应角相等可得∠DAM=∠F,全等三角形对应边相等可得EF=AD,然后根据同角的补角相等求出∠BAC=∠AEF,再利用“边角边”证明△ABC和△EAF全等,根据全等三角形对应角相等可得∠EAF=∠B,再求出∠ANB=90°,从而得证;
(2)过点E作EF∥AD交AM的延长线于F,根据两直线平行,内错角相等可得∠F=∠DAM,根据同角的余角相等求出∠EAF=∠B,然后求出∠BAC=∠AEF,再利用“角角边”证明△ABC和△EAF全等,根据全等三角形对应边可得EF=AC,然后求出EF=AD,再利用“角角边”证明△EFM和△DAM全等,根据全等三角形对应边相等可得EM=DM.
【解答】证明:(1)如图,延长AM至F,使MF=AM,
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
,
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(SAS),
∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°﹣(∠B+∠BAN)=180°﹣90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
,
∴△EFM≌△DAM(AAS),
∴EM=DM.
三角形全等的判定(第四课时)
一、选择题
1.在下列条件中,一定不能保证两直角三角形全等的是( )
A.两直角边对应相等
B.一直角边与一锐角对应相等
C.两锐角对应相等
D.斜边与一锐角对应相等
2.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS
B.SAS
C.ASA
D.AAS
3.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
4.一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
A.不能
B.带①
C.带②
D.带③
5.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=8
D.∠C=90°,AB=6
6.下列各组条件中,能判断两个直角三角形全等的是( )
A.一组边对应相等
B.两组直角边对应相等
C.两组锐角对应相等
D.一组锐角对应相等
7.如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
A.5对
B.4对
C.3对
D.2对
8.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块
B.第2块
C.第3块
D.第4块
10.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
二、填空题
11.如图所示,在△ABC中,AD⊥BC,请你添加一个条件,写出一个正确结论(不在图中添加辅助线),条件是
,结论是
.
12.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需增加的一个条件是
.
13.如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC=
.
14.在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题:
.(用题序号写)
15.△ABC中,∠A=70°,∠ABC和∠ACB的平分线相交于点P,则∠BPC=
°.
三、解答题
16.已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
17.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
18.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
19.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
20.如图所示,在△ABC中,DB=DC,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E与CD相交于点F,DH⊥BC于点H,交BE于点G,下列结论:①AD+CF=BD;②GD=FD;③CE=BF;④DH∥AF.其中正确的是
.
21.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△ABC边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
22.如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.
23.已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
参考答案与试题解析
一、选择题
1.在下列条件中,一定不能保证两直角三角形全等的是( )
A.两直角边对应相等
B.一直角边与一锐角对应相等
C.两锐角对应相等
D.斜边与一锐角对应相等
【分析】根据三角形全等的判定方法,利用直角三角形隐含的直角相等的条件,对各选项分析判断后利用排除法求解.
【解答】解:A、两直角边对应相等可以利用“SAS”证明两三角形全等,故本选项不符合题意;
B、一直角边与一锐角对应相等,可以利用“AAS”证明两三角形全等,故本选项不符合题意;
C、两锐角对应相等,不能保证两直角三角形全等,故本选项符合题意;
D、斜边与一锐角对应相等,可以利用“AAS”证明两三角形全等,故本选项不符合题意.
故选:C.
2.如图,要量湖两岸相对两点A、B的距离,可以在AB的垂线BF上取两点C、D,使CD=BC,再作出BF的垂线DE,使A、C、E在一条直线上,这时可得△ABC≌△EDC,用于判定全等的是( )
A.SSS
B.SAS
C.ASA
D.AAS
【分析】根据全等三角形的判定进行判断,注意看题目中提供了哪些证明全等的要素,要根据已知选择判断方法.
【解答】解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:C.
3.如图,用尺规法作∠DEC=∠BAC,作图痕迹的正确画法是( )
A.以点E为圆心,线段AP为半径的弧
B.以点E为圆心,线段QP为半径的弧
C.以点G为圆心,线段AP为半径的弧
D.以点G为圆心,线段QP为半径的弧
【分析】根据作一个角等于已知角的作法即可得出结论.
【解答】解:先以点A为圆心,以任意长为半径画弧,分别交AC,AB于点Q,P;
再以点E为圆心,AQ的长为半径画弧,交AC于点G,
再以点G为圆心,PQ的长为半径画弧.
故选:D.
4.一名工作人员不慎将一块三角形模具打碎成了三块,如图所示,他是否可以只带其中的一块碎片到商店去,就能买一块与原来一模一样的三角形模具呢?答案是肯定的,那么他该带哪款去?( )
A.不能
B.带①
C.带②
D.带③
【分析】根据全等三角形的判定方法结合图形判断出带③去.
【解答】解:由图形可知,③有完整的两角与夹边,根据“角边角”可以作出与原三角形全等的三角形,
所以,最省事的做法是带③去.
故选:D.
5.根据下列已知条件,能唯一画出△ABC的是( )
A.∠A=36°,∠B=45°,AB=4
B.AB=4,BC=3,∠A=30°
C.AB=3,BC=4,CA=8
D.∠C=90°,AB=6
【分析】看是否符合所学的全等的公理或定理及三角形三边关系即可.
【解答】解:A、符合全等三角形的ASA,能作出唯一三角形;
B、属于全等三角形判定中的SSA情况,不能作出唯一三角形;
C不符合三角形三边之间的关系,不能作出三角形;
D只有两个条件,不能作出唯一三角形.
故选:A.
6.下列各组条件中,能判断两个直角三角形全等的是( )
A.一组边对应相等
B.两组直角边对应相等
C.两组锐角对应相等
D.一组锐角对应相等
【分析】根据直角三角形全等的判定方法:HL、SAS、AAS、ASA分别进行分析即可.
【解答】解:A、一组边对应相等,不能判定两个直角三角形全等,故此选项错误;
B、两组直角边对应相等,可利用SAS判定两个直角三角形全等,故此选项正确;
C、两组锐角对应相等,不能判定两个直角三角形全等,故此选项错误;
D、一组锐角对应相等,不能判定两个直角三角形全等,故此选项错误;
故选:B.
7.如图,AB∥CD,AD∥BC;则图中的全等三角形共有( )
A.5对
B.4对
C.3对
D.2对
【分析】根据已知及全等三角形的判定方法进行分析,从而得到答案.
【解答】解:
∵AB∥CD,AD∥BC,
∴四边形ABCD为平行四边形,
∴AB=CD,AD=BC,AO=CO,BO=DO,EO=FO,∠DAO=∠BCO,
又∠AOB=∠COD,∠AOD=∠COB,∠AOE=∠COF,
∴△AOB≌△COD(SSS),△AOD≌△COB(SSS),△ABC≌△CDA(SSS),△ABD≌△CDB(SSS).
故图中的全等三角形共有4对.
故选:B.
8.两个三角形有两个角对应相等,正确说法是( )
A.两个三角形全等
B.两个三角形一定不全等
C.如果还有一角相等,两三角形就全等
D.如果一对等角的角平分线相等,两三角形全等
【分析】此题是一道开放性题,实则还是考查学生对三角形全等的判定方法的掌握情况.此处可以运用排除法进行分析.
【解答】解:两个三角形有两个角对应相等,那么第三个角也相等,这两个三角形的关系是全等或相似.所以排除A、B、C;
D、如果一对等角的角平分线相等,两三角形全等,符合AAS,可证三角形全等.
故选:D.
9.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1、2、3、4的四块),你认为将其中的哪一些块带去,就能配一块与原来一样大小的三角形?应该带( )
A.第1块
B.第2块
C.第3块
D.第4块
【分析】本题应先假定选择哪块,再对应三角形全等判定的条件进行验证.
【解答】解:1、3、4块玻璃不同时具备包括一完整边在内的三个证明全等的要素,所以不能带它们去,
只有第2块有完整的两角及夹边,符合ASA,满足题目要求的条件,是符合题意的.
故选:B.
10.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
【分析】锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,根据以上内容即可判断①;举出反例a=2,b=c=1,满足a+b>c,但是边长为1、1、2不能组成三角形,即可判断②;设三角形的三角为3x°,2x°,x°,由三角形的内角和定理得:3x+2x+x=180,求出3x=90,得出三角形是直角三角形,即可判断③;根据有两个角和一条边对应相等的两个三角形全等即可判断④.
【解答】解:∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;
∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;
∵设三角形的三角为3x°,2x°,x°,
∴由三角形的内角和定理得:3x+2x+x=180,
∴x=30,
3x=90,即三角形是直角三角形,∴③正确;
∵有两个角和一条边对应相等的两个三角形全等,∴④正确;
故选:C.
二、填空题
11.如图所示,在△ABC中,AD⊥BC,请你添加一个条件,写出一个正确结论(不在图中添加辅助线),条件是 AB=AC ,结论是 BD=CD .
【分析】这是一道开放性的题,只要添加一个条件并结合已知能证得结论即可.
【解答】解:∵AD⊥BC,AB=AC,
∴AD是△ABC的中线,
∴BD=CD.
故答案为:AB=AC,BD=CD.
12.在△ABC和△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需增加的一个条件是 AC=A′C′ .
【分析】本题是开放题,已知AB=A′B′,∠A=∠A′,具备了一组边和一组角分别对应相等,故添加AC=A′C′,根据SAS判定△ABC≌△A′B′C′.此题答案不唯一.
【解答】解:所添条件为:AC=A′C′.
∵AB=A′B′,∠A=∠A′,AC=A′C′
∴△ABC≌△A′B′C′(SAS).
故填AC=A′C′.
13.如图,已知BD=CE,∠B=∠C,若AB=8,AD=3,则DC= 5 .
【分析】先根据“AAS”证明△ABD≌△ACE,则AB=AC=8,然后计算AC﹣AD即可.
【解答】解:在△ABD和△ACE中
,
∴△ABD≌△ACE,
∴AB=AC=8,
∴CD=AC﹣AD=8﹣3=5.
故答案为5.
14.在△ABC和△A′B′C中,∠A=∠A′,CD与C′D′分别为AB边和A′B′边上的中线,再从以下三个条件:①AB=A′B′;②AC=A′C′;③CD=C′D′中任取两个为题设,另一个作为结论,请写出一个正确的命题: 如果①②,那么③ .(用题序号写)
【分析】根据全等三角形的判定和性质进行解答.
【解答】解:∵在△ABC和△A′B′C中,∠A=∠A′,AB=A′B′,AC=A′C′,
∴△ABC≌△A′B′C,
∴CD=C′D′.
故如果①②那么③.
15.△ABC中,∠A=70°,∠ABC和∠ACB的平分线相交于点P,则∠BPC= 125 °.
【分析】根据三角形内角和定理求出∠ABC+∠ACB,根据角平分线的定义、三角形内角和定理计算即可.
【解答】解:∵∠A=70,
∴∠ABC+∠ACB=180°﹣70°=110°,
∵∠ABC和∠ACB的平分线交于P,
∴∠PBC=∠ABC,∠PCB=ACB,
∴∠BPC=180°﹣(∠ABC+ACB)=125°,
故答案为:125.
三、解答题
16.已知,如图,△ABC为等边三角形,D是BC延长线上一点,联结AD,以AD为边作等边三角形ADE,联结CE,用你学过的知识探索AC,CD,CE三条线段之间的数量关系,试写出探究过程.
【分析】易证AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,即可求得∠BAD=∠CAE,即可证明△ABD≌△ACE,可得BD=CE,即可解题.
【解答】证明:∵△ABC和△ADE均是等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,,
∴△ABD≌△ACE,(SAS)
∴BD=CE,
∴CA+CD=CE.
17.如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可得∠ACD=∠BAC+∠ABC,∠PCD=∠P+∠PCB,根据角平分线的定义可得∠PCD=∠ACD,∠PBC=ABC,然后整理得到∠PCD=40°+∠ABC,再代入数据计算即可得解.
【解答】解:在△ABC中,∠ACD=∠BAC+∠ABC,
在△PBC中,∠PCD=∠BPC+∠PBC,
∵PB、PC分别是∠ABC和∠ACD的平分线,
∴∠PCD=∠ACD,∠PBC=∠ABC,
∴∠PCD=∠BPC+∠PBC=40°+∠ABC,
∴∠ACD=∠ABC+40°,
∴∠ACD﹣∠ABC=80°,
∴∠BAC=∠ACD﹣∠ABC=80°,
即∠CAB=80°.
∴∠CAP==50°.
18.如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,垂足为点E,以试猜想CE与BD的数量关系,并说明理由.
【分析】延长BA、CE相交于点F,利用“角边角”证明△BCE和△BFE全等,根据全等三角形对应边相等可得CE=EF,根据等角的余角相等求出∠ABD=∠ACF,然后利用“角边角”证明△ABD和△ACF全等,根据全等三角形对应边相等可得BD=CF,然后求解即可.
【解答】解:BD=2CE.
理由如下:如图,延长BA、CE相交于点F,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△BCE和△BFE中,,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∵∠BAC=90°,CE⊥BD,
∴∠ACF+∠F=90°,∠ABD+∠F=90°,
∴∠ABD=∠ACF,
在△ABD和△ACF中,,
∴△ABD≌△ACF(ASA),
∴BD=CF,
∵CF=CE+EF=2CE,
∴BD=2CE.
19.CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE = CF;EF = |BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件 ∠α+∠BCA=180° ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
【分析】由题意推出∠CBE=∠ACF,再由AAS定理证△BCE≌△CAF,继而得答案.
【解答】解:(1)①∵∠BCA=90°,∠α=90°,
∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,
∴∠CBE=∠ACF,
∵CA=CB,∠BEC=∠CFA;
∴△BCE≌△CAF,
∴BE=CF;EF=|CF﹣CE|=|BE﹣AF|.
②所填的条件是:∠α+∠BCA=180°.
证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.
∵∠BCA=180°﹣∠α,
∴∠CBE+∠BCE=∠BCA.
又∵∠ACF+∠BCE=∠BCA,
∴∠CBE=∠ACF,
又∵BC=CA,∠BEC=∠CFA,
∴△BCE≌△CAF(AAS)
∴BE=CF,CE=AF,
又∵EF=CF﹣CE,
∴EF=|BE﹣AF|.
(2)猜想:EF=BE+AF.
证明过程:
∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,
∴∠BCE=∠CAF,
又∵BC=CA,
∴△BCE≌△CAF(AAS).
∴BE=CF,EC=FA,
∴EF=EC+CF=BE+AF.
20.如图所示,在△ABC中,DB=DC,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E与CD相交于点F,DH⊥BC于点H,交BE于点G,下列结论:①AD+CF=BD;②GD=FD;③CE=BF;④DH∥AF.其中正确的是 ①②③④ .
【分析】通过证明△ABE≌△CBE,△ADC≌△FDB,可得AE=EC,BF=AC,AD=DF,利用等腰三角形的性质和直角三角形的性质依次判断可求解.
【解答】解:∵DB=DC,CD⊥AB,
∴∠DBC=∠DCB=45°,
∵BE平分∠ABC,
∴∠DBF=∠CBF=22.5°,
∵DH⊥BC,
∴∠DHB=∠BDC=90°,
∴∠BGH=67.5°=∠DFB,
∴∠DFB=∠DGF,
∴DG=DF,故②正确,
∵∠ABE=∠CBE,BE=BE,∠AEB=∠CEB,
∴△ABE≌△CBE(ASA),
∴AE=EC,
∵∠CAD+∠ACD=90°,∠CAD+∠ABE=90°,
∴∠ACD=∠ABE,
又∵BD=CD,∠BDF=∠CDA=90°,
∴△ADC≌△FDB(AAS),
∴BF=AC,AD=DF,
∴AD+CF=DF+CF=BD,故①正确;
∵AC=2CE,
∴CE=AC=BF,故③正确,
∵DB=DC,∠BDC=90°,DH⊥BC,
∴∠CDH=45°,
∵AD=DF,∠ADF=90°,
∴∠AFD=45°=∠CDH,
∴AF∥DH,故④正确,
故答案为:①②③④.
21.(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△ABC边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
【分析】(1)根据等边三角形的三条边、三个内角都相等的性质,利用全等三角形的判定定理SAS可以证得△BCD≌△ACF;然后由全等三角形的对应边相等知AF=BD;
(2)通过证明△BCD≌△ACF,即可证明AF=BD;
(3)Ⅰ.AF+BF′=AB;利用全等三角形△BCD≌△ACF(SAS)的对应边BD=AF;同理△BCF′≌△ACD(SAS),则BF′=AD,所以AF+BF′=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;通过证明△BCF′≌△ACD(SAS),则BF′=AD(全等三角形的对应边相等);再结合(2)中的结论即可证得AF=AB+BF′.
【解答】解:(1)AF=BD;
证明如下:∵△ABC是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质);
同理知,DC=CF,∠DCF=60°;
∴∠BCA﹣∠DCA=∠DCF﹣∠DCA,即∠BCD=∠ACF;
在△BCD和△ACF中,
,
∴△BCD≌△ACF(SAS),
∴BD=AF(全等三角形的对应边相等);
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立;
(3)Ⅰ.AF+BF′=AB;
证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD(SAS),则BF′=AD,
∴AF+BF′=BD+AD=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′;
证明如下:在△BCF′和△ACD中,
,
∴△BCF′≌△ACD(SAS),
∴BF′=AD(全等三角形的对应边相等);
又由(2)知,AF=BD;
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
22.如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.
(1)当直线l经过点C时(如图2),求证:BN=CD;
(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;
(3)请直接写出BN、CE、CD之间的等量关系.
【分析】(1)连接ND,先由已知条件证明DN=DC,再证明BN=DN即可;
(2)当M是BC中点时,CE和CD之间的等量关系为CD=2CE,过点C作CN'⊥AO交AB于N'.过点C作CG∥AB交直线l于G,再证明△BNM≌△CGM问题得证;
(3)BN、CE、CD之间的等量关系要分三种情况讨论:①当点M在线段BC上时;②当点M在BC的延长线上时;③当点M在CB的延长线上时;由(2)即可得出结论.
【解答】(1)证明:连接ND,如图2所示:
∵AO平分∠BAC,
∴∠BAD=∠CAD,
∵直线l⊥AO于H,
∴∠AHN=∠AHE=90°,
∴∠ANH=∠AEH,
∴AN=AC,
∴NH=CH,
∴AH是线段NC的中垂线,
∴DN=DC,
∴∠DNH=∠DCH,
∴∠AND=∠ACB,
∵∠AND=∠B+∠BDN,∠ACB=2∠B,
∴∠B=∠BDN,
∴BN=DN,
∴BN=DC;
(2)解:当M是BC中点时,CE和CD之间的等量关系为CD=2CE,理由如下:
过点C作CN'⊥AO交AB于N',过点C作CG∥AB交直线l于点G,如图3所示:
由(1)得:BN'=CD,AN'=AC,AN=AE,
∴∠ANE=∠AEN,NN'=CE,
∴∠ANE=∠CGE,∠B=∠BCG,
∴∠CGE=∠AEN,
∴CG=CE,
∵M是BC中点,
∴BM=CM,
在△BNM和△CGM中,,
∴△BNM≌△CGM(ASA),
∴BN=CG,
∴BN=CE,
∴CD=BN'=NN'+BN=2CE;
(3)解:BN、CE、CD之间的等量关系:当点M在线段BC上时,CD=BN+CE;理由如下:
过点C作CN'⊥AO交AB于N',如图3所示:
由(2)得:NN'=CE,CD=BN'=BN+CE;
当点M在BC的延长线上时,CD=BN﹣CE;理由如下:
过点C作CN'⊥AO交AB于N',如图4所示:
同(2)得:NN'=CE,CD=BN'=BN﹣CE;
当点M在CB的延长线上时,CD=CE﹣BN;理由如下:
过点C作CN'⊥AO交AB于N',如图5所示:
同(2)得:NN'=CE,CD=BN'=CE﹣BN.
23.已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
【分析】(1)延长AM至F,使MF=AM,然后利用“边角边”证明△EMF和△DMA全等,根据全等三角形对应角相等可得∠DAM=∠F,全等三角形对应边相等可得EF=AD,然后根据同角的补角相等求出∠BAC=∠AEF,再利用“边角边”证明△ABC和△EAF全等,根据全等三角形对应角相等可得∠EAF=∠B,再求出∠ANB=90°,从而得证;
(2)过点E作EF∥AD交AM的延长线于F,根据两直线平行,内错角相等可得∠F=∠DAM,根据同角的余角相等求出∠EAF=∠B,然后求出∠BAC=∠AEF,再利用“角角边”证明△ABC和△EAF全等,根据全等三角形对应边可得EF=AC,然后求出EF=AD,再利用“角角边”证明△EFM和△DAM全等,根据全等三角形对应边相等可得EM=DM.
【解答】证明:(1)如图,延长AM至F,使MF=AM,
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
,
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(SAS),
∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°﹣(∠B+∠BAN)=180°﹣90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°﹣90°×2﹣∠DAE=180°﹣∠DAE,
∵∠AEF=180°﹣∠F﹣∠EAM=180°﹣∠DAM﹣∠EAM=180°﹣∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
,
∴△EFM≌△DAM(AAS),
∴EM=DM.
