11.3.1 多边形 同步练习 2021-2022学年人教版八年级数学上册(word版含答案)
文档属性
| 名称 | 11.3.1 多边形 同步练习 2021-2022学年人教版八年级数学上册(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 08:25:25 | ||
图片预览



文档简介
11.3.1
多边形
一、单选题
1.若一个多边形从一个顶点可以引出3条对角线,则它是( )边形.
A.五
B.六
C.七
D.八
2.下列说法中,正确的是( )
A.直线有两个端点
B.射线有两个端点
C.有六边相等的多边形叫做正六边形
D.有公共端点的两条射线组成的图形叫做角
3.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n
B.(n﹣1)
C.(n﹣2)
D.(n﹣3)
4.过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
5.如果过一个多边形的一个顶点的对角线有7条,则该多边形是( )
A.十边形
B.九边形
C.八边形
D.七边形
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
A.8
B.9
C.10
D.11
7.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16
B.17
C.18
D.19
8.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
9.一个正十边形的某一边长为8cm,其中一个内角的度数为144°,则这个正十边形的周长和内角和分别为( )
A.64cm,1440°
B.80cm,1620°
C.80cm,1440°
D.88cm,1620°
10.通过连接对角线的方法,可以把十边形分成互不重叠的三角形的个数( )
A.7个
B.8个
C.9个
D.10个
二、填空题
11.从八边形的一个顶点可以引
条对角线,八边形总共有
条对角线.
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画
条对角线.
13.将一个正方形截去(至少)一个角,则其边数
.
14.以线段a=7,b=8,c=9,d=11为边作四边形,可作 个.
15.一个四边形剪去一三角形后余下的多边形为
边形.
三、解答题
16.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
17.一个多边形的内角和是外角和的3倍,求这个多边形的边数.
18.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:
(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
19.(1)如图①,O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
(2)如图②,O在五边形ABCDE的边AB上,连接OC、OD、OE可以得几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
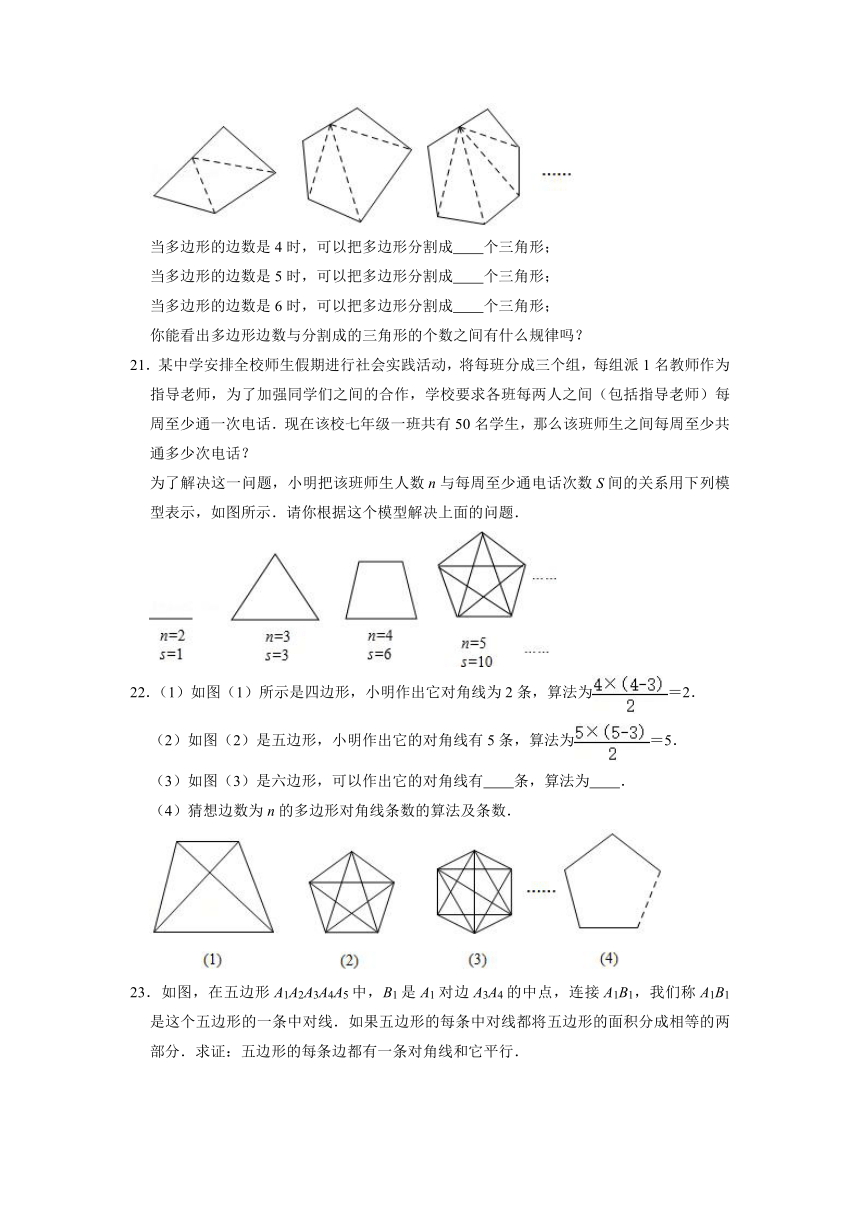
20.从一个多边形一边上的一点(不是顶点)出发,分别连接这个点与各个顶点,可以把这个多边形分割成若干个三角形,请你观察下图,并完成后面的填空.
当多边形的边数是4时,可以把多边形分割成 个三角形;
当多边形的边数是5时,可以把多边形分割成 个三角形;
当多边形的边数是6时,可以把多边形分割成 个三角形;
你能看出多边形边数与分割成的三角形的个数之间有什么规律吗?
21.某中学安排全校师生假期进行社会实践活动,将每班分成三个组,每组派1名教师作为指导老师,为了加强同学们之间的合作,学校要求各班每两人之间(包括指导老师)每周至少通一次电话.现在该校七年级一班共有50名学生,那么该班师生之间每周至少共通多少次电话?
为了解决这一问题,小明把该班师生人数n与每周至少通电话次数S间的关系用下列模型表示,如图所示.请你根据这个模型解决上面的问题.
22.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有 条,算法为 .
(4)猜想边数为n的多边形对角线条数的算法及条数.
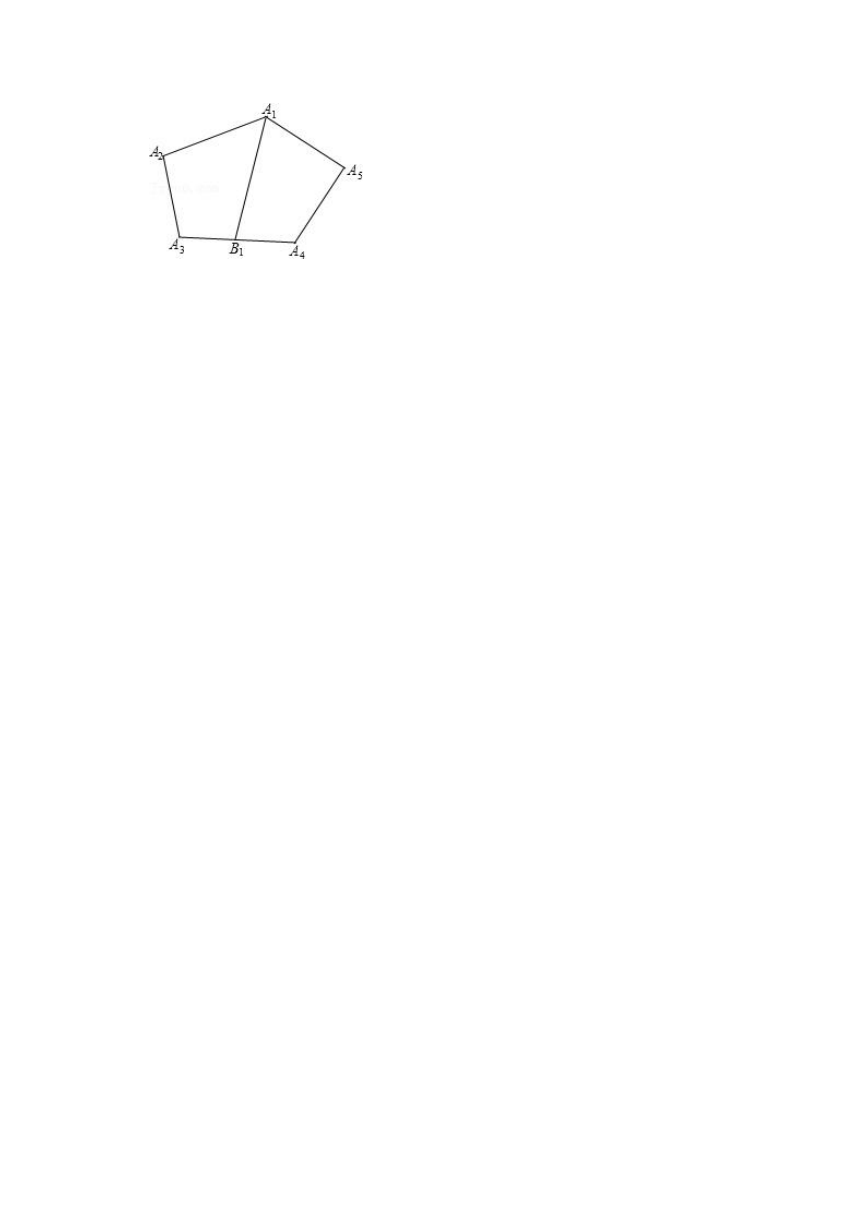
23.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
参考答案与试题解析
一、单选题
1.若一个多边形从一个顶点可以引出3条对角线,则它是( )边形.
A.五
B.六
C.七
D.八
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线可得答案.
【解答】解:设这个多边形有n条边,由题意得:
n﹣3=3,
解得:n=6,
故选:B.
2.下列说法中,正确的是( )
A.直线有两个端点
B.射线有两个端点
C.有六边相等的多边形叫做正六边形
D.有公共端点的两条射线组成的图形叫做角
【分析】根据直线、射线的性质,正多边形的性质,角的定义,可得答案.
【解答】解:A、直线没有端点;
B、射线有一个端点;
C、六条边相等,故C错误;
D、有公共端点的两条射线组成的图形叫做角;
故选:D.
3.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n
B.(n﹣1)
C.(n﹣2)
D.(n﹣3)
【分析】可根据n边形从一个顶点引出的对角线与边的关系:n﹣3,可分成(n﹣2)个三角形直接判断.
【解答】解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n﹣2).
故选:C.
4.过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
【分析】n边形中过一个顶点的所有对角线有(n﹣3)条,把这个多边形分成(n﹣2)个三角形,根据这一点即可解答.
【解答】解:这个多边形的边数是4+2=4.
故选:D.
5.如果过一个多边形的一个顶点的对角线有7条,则该多边形是( )
A.十边形
B.九边形
C.八边形
D.七边形
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线进行解答即可.
【解答】解:设这个多边形边数为n,由题意得:
n﹣3=7,
解得:n=10.
故选:A.
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
A.8
B.9
C.10
D.11
【分析】可根据多边形过一个顶点的对角线与分成的三角形的个数的关系列方程求解.
【解答】解:设多边形有n条边,
则n﹣2=11,解得n=13.
故这个多边形是十三边形.
故经过这一点的对角线的条数是13﹣3=10.
故选:C.
7.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16
B.17
C.18
D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
【解答】解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
8.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
【分析】根据正多边形的判定与性质对各个选项分别判断即可.
【解答】解:∵各边都相等、各内角都相等的多边形是正多边形,
∴选项A符合题意;
∵正多形的各边都相等,
∴选项B不符合题意;
∵正三角形就是等边三角形,
∴选项C不符合题意;
∵各内角相等的多边形不一定是正多边形,
∴选项D不符合题意;
故选:A.
9.一个正十边形的某一边长为8cm,其中一个内角的度数为144°,则这个正十边形的周长和内角和分别为( )
A.64cm,1440°
B.80cm,1620°
C.80cm,1440°
D.88cm,1620°
【分析】正多边形的每个角都相等,同样每个外角也相等,一个内角是144°,则外角是180°﹣144°=36°.又已知多边形的外角和是360度,由此即可求得多边形的边数,利用边数乘以内角的度数即可求得内角和度数.
【解答】解:这个正十边形的周长是8cm×10=80cm.
内角和是:144×10=1440°.
故选:C.
10.通过连接对角线的方法,可以把十边形分成互不重叠的三角形的个数( )
A.7个
B.8个
C.9个
D.10个
【分析】从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n﹣2)个三角形,依此作答.
【解答】解:从十边形的一个顶点出发所引的所有对角线可以将其分为10﹣2=8个三角形.
故选:B.
二、填空题
11.从八边形的一个顶点可以引 5 条对角线,八边形总共有 20 条对角线.
【分析】n边形从一个顶点出发可引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,n边形对角线的总条数为n(n﹣3).
【解答】解:八边形从一个顶点出发可以引8﹣3=5条对角线,八边形共有.
故答案为:8,20.
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画 5 条对角线.
【分析】利用多边形外角和除以外角的度数可得正多边形的边数,再利用边数减3可得答案.
【解答】解:正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8﹣5=5,
故答案为:5.
13.将一个正方形截去(至少)一个角,则其边数 可能增加,也可能减少,也可能不变 .
【分析】一个正方形截去一个角是指可以截去两条边,而新增一条边,得到三角形;也可以截去一条边,而新增一条边,得到四边形;也可以直接新增一条边,变为五边形.可动手画一画,具体操作一下.
【解答】解:如图可知,一个正方形截去一个角后变成三角形或四边形或五边形.
故其边数可能增加,也可能减少.
故答案为:可能增加,也可能减少.
14.以线段a=7,b=8,c=9,d=11为边作四边形,可作 个.
【分析】根据四边形具有不稳定性,可知四条线段组成的四边形可有无数种变化.
【解答】解:四条线段组成的四边形可有无数种变化.
故答案为:无数.
15.一个四边形剪去一三角形后余下的多边形为 三、四、五 边形.
【分析】分四边形剪去一个角,边数减少1,不变,增加1,即可得解.
【解答】解:一个四边形剪去一三角形后余下的多边形为三边形或四边形或五边形.
故答案为:三、四、五.
三、解答题
16.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
【分析】(1)边长=周长÷边数;
(2)分别表示出a和b的代数式,让其相等,看是否有相应的值.
【解答】解:(1)a=20;
(2)此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得,即.
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
17.一个多边形的内角和是外角和的3倍,求这个多边形的边数.
【分析】根据多边形的外角和为360°,内角和公式为:(n﹣2)?180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
【解答】解:设这个多边形是n边形,由题意得:
(n﹣2)×180°=360°×3,
解得:n=7.
答:这个多边形的边数是8.
18.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:
(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
【分析】把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边.于是,当将原多边形分割成4个小多边形,最多可以增加4×3=12条边,当将原多边形分割成8个小多边形,最少可以增加2×7=14条边.所以分割后的多边形的个数是5,6,7中的一个.设原多边形的边数是n,分割成边数为a1,a2,…,am的m个多边形,则m个多边形的总边数为a1+a2+…+am由题意,可得方程a1+a2+…+am=n+13,
180(a1﹣2)+180(a2﹣2)+…+180(am﹣2)=1.3×180(n﹣2),再整理可得3n+20m=156,再讨论出二元一次方程的整数解即可.
【解答】解:设原多边形的边数是n,分割成边数为a1,a2,…,am的m个多边形,则m个多边形的总边数为a6+a2+…+am,由题意有
a1+a8+…+am=n+13,
180(a1﹣2)+180(a2﹣2)+…+180(am﹣2)=3.3×180(n﹣2),
则4n+20m=156,
解得:m=6,n=12.
故原来的多边形是12边形,把原来的多边形分割成了6个小多边形.
19.(1)如图①,O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
(2)如图②,O在五边形ABCDE的边AB上,连接OC、OD、OE可以得几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
【分析】(1)根据图形可以得4个三角形,它与边数相等,
(2)根据图形可以得4个三角形,它的个数比边数小1,
(3)根据图形可以得到4个三角形,它的个数比边数小2.
【解答】解:(1)连接OA、OB、OD可以得4个三角形,
(2)连接OC、OD,它的个数比边数小1,
(3)过点A作六边形ABCDEF的对角线,可以得到7个三角形.
20.从一个多边形一边上的一点(不是顶点)出发,分别连接这个点与各个顶点,可以把这个多边形分割成若干个三角形,请你观察下图,并完成后面的填空.
当多边形的边数是4时,可以把多边形分割成 个三角形;
当多边形的边数是5时,可以把多边形分割成 个三角形;
当多边形的边数是6时,可以把多边形分割成 个三角形;
你能看出多边形边数与分割成的三角形的个数之间有什么规律吗?
【分析】依据图形即可得到三角形的个数以及多边形边数与分割成的三角形的个数之间的关系.
【解答】解:当多边形的边数是4时,可以把多边形分割成3个三角形;
当多边形的边数是5时,可以把多边形分割成4个三角形;
当多边形的边数是6时,可以把多边形分割成5个三角形;
由题可得,多边形的边数比分割成的三角形的个数多1.
故答案为:3,4,5.
21.某中学安排全校师生假期进行社会实践活动,将每班分成三个组,每组派1名教师作为指导老师,为了加强同学们之间的合作,学校要求各班每两人之间(包括指导老师)每周至少通一次电话.现在该校七年级一班共有50名学生,那么该班师生之间每周至少共通多少次电话?
为了解决这一问题,小明把该班师生人数n与每周至少通电话次数S间的关系用下列模型表示,如图所示.请你根据这个模型解决上面的问题.
【分析】根据模型得到n个同学和老师之间共通话次,代入n=53求解即可.
【解答】1378次解:观察图形发现第n个图案中s=,
当n=53时,s==1378次,
所以53个同学和老师至少通话1378次.
22.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有 条,算法为 .
(4)猜想边数为n的多边形对角线条数的算法及条数.
【分析】根据(1)(2)所给算法计算即可.
【解答】解:(3)六边形,可以作出它的对角线有9条,算法:=9;
故答案为:9;=9;
(4)n的多边形对角线条数的算法及条数.
23.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
【分析】可以再做五边形的一条中对线,根据它们分割成的两部分的面积相等,都是五边形的面积的一半,导出两个等底的三角形的面积相等,从而得到它们的高相等,则得到五边形的每条边都有一条对角线和它平行.
【解答】证明:取A1A5中点B3,连接A3B3、A1A3、A1A4、A3A5,
∵A3B1=B1A4,
∴S△A1A3B1=S△A1B1A4,
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等,
∴S△A1A2A3=S△A1A4A5,
同理S△A1A2A3=S△A3A4A5,
∴S△A1A4A5=S△A3A4A5,
∴△A3A4A5与△A1A4A5边A4A5上的高相等,
∴A1A3∥A4A5,
同理可证A1A2∥A3A5,A2A3∥A1A4,A3A4∥A2A5,A5A1∥A2A4.
多边形
一、单选题
1.若一个多边形从一个顶点可以引出3条对角线,则它是( )边形.
A.五
B.六
C.七
D.八
2.下列说法中,正确的是( )
A.直线有两个端点
B.射线有两个端点
C.有六边相等的多边形叫做正六边形
D.有公共端点的两条射线组成的图形叫做角
3.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n
B.(n﹣1)
C.(n﹣2)
D.(n﹣3)
4.过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
5.如果过一个多边形的一个顶点的对角线有7条,则该多边形是( )
A.十边形
B.九边形
C.八边形
D.七边形
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
A.8
B.9
C.10
D.11
7.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16
B.17
C.18
D.19
8.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
9.一个正十边形的某一边长为8cm,其中一个内角的度数为144°,则这个正十边形的周长和内角和分别为( )
A.64cm,1440°
B.80cm,1620°
C.80cm,1440°
D.88cm,1620°
10.通过连接对角线的方法,可以把十边形分成互不重叠的三角形的个数( )
A.7个
B.8个
C.9个
D.10个
二、填空题
11.从八边形的一个顶点可以引
条对角线,八边形总共有
条对角线.
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画
条对角线.
13.将一个正方形截去(至少)一个角,则其边数
.
14.以线段a=7,b=8,c=9,d=11为边作四边形,可作 个.
15.一个四边形剪去一三角形后余下的多边形为
边形.
三、解答题
16.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
17.一个多边形的内角和是外角和的3倍,求这个多边形的边数.
18.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:
(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
19.(1)如图①,O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
(2)如图②,O在五边形ABCDE的边AB上,连接OC、OD、OE可以得几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
20.从一个多边形一边上的一点(不是顶点)出发,分别连接这个点与各个顶点,可以把这个多边形分割成若干个三角形,请你观察下图,并完成后面的填空.
当多边形的边数是4时,可以把多边形分割成 个三角形;
当多边形的边数是5时,可以把多边形分割成 个三角形;
当多边形的边数是6时,可以把多边形分割成 个三角形;
你能看出多边形边数与分割成的三角形的个数之间有什么规律吗?
21.某中学安排全校师生假期进行社会实践活动,将每班分成三个组,每组派1名教师作为指导老师,为了加强同学们之间的合作,学校要求各班每两人之间(包括指导老师)每周至少通一次电话.现在该校七年级一班共有50名学生,那么该班师生之间每周至少共通多少次电话?
为了解决这一问题,小明把该班师生人数n与每周至少通电话次数S间的关系用下列模型表示,如图所示.请你根据这个模型解决上面的问题.
22.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有 条,算法为 .
(4)猜想边数为n的多边形对角线条数的算法及条数.
23.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
参考答案与试题解析
一、单选题
1.若一个多边形从一个顶点可以引出3条对角线,则它是( )边形.
A.五
B.六
C.七
D.八
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线可得答案.
【解答】解:设这个多边形有n条边,由题意得:
n﹣3=3,
解得:n=6,
故选:B.
2.下列说法中,正确的是( )
A.直线有两个端点
B.射线有两个端点
C.有六边相等的多边形叫做正六边形
D.有公共端点的两条射线组成的图形叫做角
【分析】根据直线、射线的性质,正多边形的性质,角的定义,可得答案.
【解答】解:A、直线没有端点;
B、射线有一个端点;
C、六条边相等,故C错误;
D、有公共端点的两条射线组成的图形叫做角;
故选:D.
3.从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是( )
A.n
B.(n﹣1)
C.(n﹣2)
D.(n﹣3)
【分析】可根据n边形从一个顶点引出的对角线与边的关系:n﹣3,可分成(n﹣2)个三角形直接判断.
【解答】解:从n边形的一个顶点作对角线,把这个n边形分成三角形的个数是(n﹣2).
故选:C.
4.过一个多边形的一个顶点的所有对角线把多边形分成4个三角形,则这个多边形的边数为( )
A.3
B.4
C.5
D.6
【分析】n边形中过一个顶点的所有对角线有(n﹣3)条,把这个多边形分成(n﹣2)个三角形,根据这一点即可解答.
【解答】解:这个多边形的边数是4+2=4.
故选:D.
5.如果过一个多边形的一个顶点的对角线有7条,则该多边形是( )
A.十边形
B.九边形
C.八边形
D.七边形
【分析】根据n边形从一个顶点出发可引出(n﹣3)条对角线进行解答即可.
【解答】解:设这个多边形边数为n,由题意得:
n﹣3=7,
解得:n=10.
故选:A.
6.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是( )
A.8
B.9
C.10
D.11
【分析】可根据多边形过一个顶点的对角线与分成的三角形的个数的关系列方程求解.
【解答】解:设多边形有n条边,
则n﹣2=11,解得n=13.
故这个多边形是十三边形.
故经过这一点的对角线的条数是13﹣3=10.
故选:C.
7.把一个多边形纸片沿一条直线截下一个三角形后,变成一个18边形,则原多边形纸片的边数不可能是( )
A.16
B.17
C.18
D.19
【分析】一个n边形剪去一个角后,剩下的形状可能是n边形或(n+1)边形或(n﹣1)边形.
【解答】解:当剪去一个角后,剩下的部分是一个18边形,
则这张纸片原来的形状可能是18边形或17边形或19边形,不可能是16边形.
故选:A.
8.下列说法不正确的是( )
A.各边都相等的多边形是正多边形
B.正多边形的各边都相等
C.正三角形就是等边三角形
D.各内角相等的多边形不一定是正多边形
【分析】根据正多边形的判定与性质对各个选项分别判断即可.
【解答】解:∵各边都相等、各内角都相等的多边形是正多边形,
∴选项A符合题意;
∵正多形的各边都相等,
∴选项B不符合题意;
∵正三角形就是等边三角形,
∴选项C不符合题意;
∵各内角相等的多边形不一定是正多边形,
∴选项D不符合题意;
故选:A.
9.一个正十边形的某一边长为8cm,其中一个内角的度数为144°,则这个正十边形的周长和内角和分别为( )
A.64cm,1440°
B.80cm,1620°
C.80cm,1440°
D.88cm,1620°
【分析】正多边形的每个角都相等,同样每个外角也相等,一个内角是144°,则外角是180°﹣144°=36°.又已知多边形的外角和是360度,由此即可求得多边形的边数,利用边数乘以内角的度数即可求得内角和度数.
【解答】解:这个正十边形的周长是8cm×10=80cm.
内角和是:144×10=1440°.
故选:C.
10.通过连接对角线的方法,可以把十边形分成互不重叠的三角形的个数( )
A.7个
B.8个
C.9个
D.10个
【分析】从n边形的一个顶点出发,连接这个点与其余各顶点,可以把一个多边形分割成(n﹣2)个三角形,依此作答.
【解答】解:从十边形的一个顶点出发所引的所有对角线可以将其分为10﹣2=8个三角形.
故选:B.
二、填空题
11.从八边形的一个顶点可以引 5 条对角线,八边形总共有 20 条对角线.
【分析】n边形从一个顶点出发可引出(n﹣3)条对角线,把n边形分成(n﹣2)个三角形,n边形对角线的总条数为n(n﹣3).
【解答】解:八边形从一个顶点出发可以引8﹣3=5条对角线,八边形共有.
故答案为:8,20.
12.若一个多边形的每个外角都是45°,则从这个多边形的一个顶点出发可以画 5 条对角线.
【分析】利用多边形外角和除以外角的度数可得正多边形的边数,再利用边数减3可得答案.
【解答】解:正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8﹣5=5,
故答案为:5.
13.将一个正方形截去(至少)一个角,则其边数 可能增加,也可能减少,也可能不变 .
【分析】一个正方形截去一个角是指可以截去两条边,而新增一条边,得到三角形;也可以截去一条边,而新增一条边,得到四边形;也可以直接新增一条边,变为五边形.可动手画一画,具体操作一下.
【解答】解:如图可知,一个正方形截去一个角后变成三角形或四边形或五边形.
故其边数可能增加,也可能减少.
故答案为:可能增加,也可能减少.
14.以线段a=7,b=8,c=9,d=11为边作四边形,可作 个.
【分析】根据四边形具有不稳定性,可知四条线段组成的四边形可有无数种变化.
【解答】解:四条线段组成的四边形可有无数种变化.
故答案为:无数.
15.一个四边形剪去一三角形后余下的多边形为 三、四、五 边形.
【分析】分四边形剪去一个角,边数减少1,不变,增加1,即可得解.
【解答】解:一个四边形剪去一三角形后余下的多边形为三边形或四边形或五边形.
故答案为:三、四、五.
三、解答题
16.已知正n边形的周长为60,边长为a
(1)当n=3时,请直接写出a的值;
(2)把正n边形的周长与边数同时增加7后,假设得到的仍是正多边形,它的边数为n+7,周长为67,边长为b.有人分别取n等于3,20,120,再求出相应的a与b,然后断言:“无论n取任何大于2的正整数,a与b一定不相等.”你认为这种说法对吗?若不对,请求出不符合这一说法的n的值.
【分析】(1)边长=周长÷边数;
(2)分别表示出a和b的代数式,让其相等,看是否有相应的值.
【解答】解:(1)a=20;
(2)此说法不正确.
理由如下:尽管当n=3、20、120时,a>b或a<b,
但可令a=b,得,即.
∴60n+420=67n,
解得n=60,
经检验n=60是方程的根.
∴当n=60时,a=b,即不符合这一说法的n的值为60.
17.一个多边形的内角和是外角和的3倍,求这个多边形的边数.
【分析】根据多边形的外角和为360°,内角和公式为:(n﹣2)?180°,由题意可知:内角和=3×外角和,设出未知数,可得到方程,解方程即可.
【解答】解:设这个多边形是n边形,由题意得:
(n﹣2)×180°=360°×3,
解得:n=7.
答:这个多边形的边数是8.
18.把一个多边形沿着几条直线剪开,分割成若干个多边形.分割后的多边形的边数总和比原多边形的边数多13条,内角和是原多边形内角和的1.3倍.求:
(1)原来的多边形是几边形?
(2)把原来的多边形分割成了多少个多边形?
【分析】把多边形沿直线剪开,每增加一个多边形,边数的增加会出现以下三种情况:①当直线经过两个顶点时,增加两条边;②当直线经过一个顶点时,增加三条边;③当直线不经过顶点时,增加四条边.于是,当将原多边形分割成4个小多边形,最多可以增加4×3=12条边,当将原多边形分割成8个小多边形,最少可以增加2×7=14条边.所以分割后的多边形的个数是5,6,7中的一个.设原多边形的边数是n,分割成边数为a1,a2,…,am的m个多边形,则m个多边形的总边数为a1+a2+…+am由题意,可得方程a1+a2+…+am=n+13,
180(a1﹣2)+180(a2﹣2)+…+180(am﹣2)=1.3×180(n﹣2),再整理可得3n+20m=156,再讨论出二元一次方程的整数解即可.
【解答】解:设原多边形的边数是n,分割成边数为a1,a2,…,am的m个多边形,则m个多边形的总边数为a6+a2+…+am,由题意有
a1+a8+…+am=n+13,
180(a1﹣2)+180(a2﹣2)+…+180(am﹣2)=3.3×180(n﹣2),
则4n+20m=156,
解得:m=6,n=12.
故原来的多边形是12边形,把原来的多边形分割成了6个小多边形.
19.(1)如图①,O为四边形ABCD内一点,连接OA、OB、OC、OD可以得几个三角形?它与边数有何关系?
(2)如图②,O在五边形ABCDE的边AB上,连接OC、OD、OE可以得几个三角形?它与边数有何关系?
(3)如图③,过点A作六边形ABCDEF的对角线,可以得到几个三角形?它与边数有何关系?
【分析】(1)根据图形可以得4个三角形,它与边数相等,
(2)根据图形可以得4个三角形,它的个数比边数小1,
(3)根据图形可以得到4个三角形,它的个数比边数小2.
【解答】解:(1)连接OA、OB、OD可以得4个三角形,
(2)连接OC、OD,它的个数比边数小1,
(3)过点A作六边形ABCDEF的对角线,可以得到7个三角形.
20.从一个多边形一边上的一点(不是顶点)出发,分别连接这个点与各个顶点,可以把这个多边形分割成若干个三角形,请你观察下图,并完成后面的填空.
当多边形的边数是4时,可以把多边形分割成 个三角形;
当多边形的边数是5时,可以把多边形分割成 个三角形;
当多边形的边数是6时,可以把多边形分割成 个三角形;
你能看出多边形边数与分割成的三角形的个数之间有什么规律吗?
【分析】依据图形即可得到三角形的个数以及多边形边数与分割成的三角形的个数之间的关系.
【解答】解:当多边形的边数是4时,可以把多边形分割成3个三角形;
当多边形的边数是5时,可以把多边形分割成4个三角形;
当多边形的边数是6时,可以把多边形分割成5个三角形;
由题可得,多边形的边数比分割成的三角形的个数多1.
故答案为:3,4,5.
21.某中学安排全校师生假期进行社会实践活动,将每班分成三个组,每组派1名教师作为指导老师,为了加强同学们之间的合作,学校要求各班每两人之间(包括指导老师)每周至少通一次电话.现在该校七年级一班共有50名学生,那么该班师生之间每周至少共通多少次电话?
为了解决这一问题,小明把该班师生人数n与每周至少通电话次数S间的关系用下列模型表示,如图所示.请你根据这个模型解决上面的问题.
【分析】根据模型得到n个同学和老师之间共通话次,代入n=53求解即可.
【解答】1378次解:观察图形发现第n个图案中s=,
当n=53时,s==1378次,
所以53个同学和老师至少通话1378次.
22.(1)如图(1)所示是四边形,小明作出它对角线为2条,算法为=2.
(2)如图(2)是五边形,小明作出它的对角线有5条,算法为=5.
(3)如图(3)是六边形,可以作出它的对角线有 条,算法为 .
(4)猜想边数为n的多边形对角线条数的算法及条数.
【分析】根据(1)(2)所给算法计算即可.
【解答】解:(3)六边形,可以作出它的对角线有9条,算法:=9;
故答案为:9;=9;
(4)n的多边形对角线条数的算法及条数.
23.如图,在五边形A1A2A3A4A5中,B1是A1对边A3A4的中点,连接A1B1,我们称A1B1是这个五边形的一条中对线.如果五边形的每条中对线都将五边形的面积分成相等的两部分.求证:五边形的每条边都有一条对角线和它平行.
【分析】可以再做五边形的一条中对线,根据它们分割成的两部分的面积相等,都是五边形的面积的一半,导出两个等底的三角形的面积相等,从而得到它们的高相等,则得到五边形的每条边都有一条对角线和它平行.
【解答】证明:取A1A5中点B3,连接A3B3、A1A3、A1A4、A3A5,
∵A3B1=B1A4,
∴S△A1A3B1=S△A1B1A4,
又∵四边形A1A2A3B1与四边形A1B1A4A5的面积相等,
∴S△A1A2A3=S△A1A4A5,
同理S△A1A2A3=S△A3A4A5,
∴S△A1A4A5=S△A3A4A5,
∴△A3A4A5与△A1A4A5边A4A5上的高相等,
∴A1A3∥A4A5,
同理可证A1A2∥A3A5,A2A3∥A1A4,A3A4∥A2A5,A5A1∥A2A4.
