13.1.1轴对称 同步练习题 2021-2022学年人教版八年级数学上册(Word版含答案)
文档属性
| 名称 | 13.1.1轴对称 同步练习题 2021-2022学年人教版八年级数学上册(Word版含答案) | 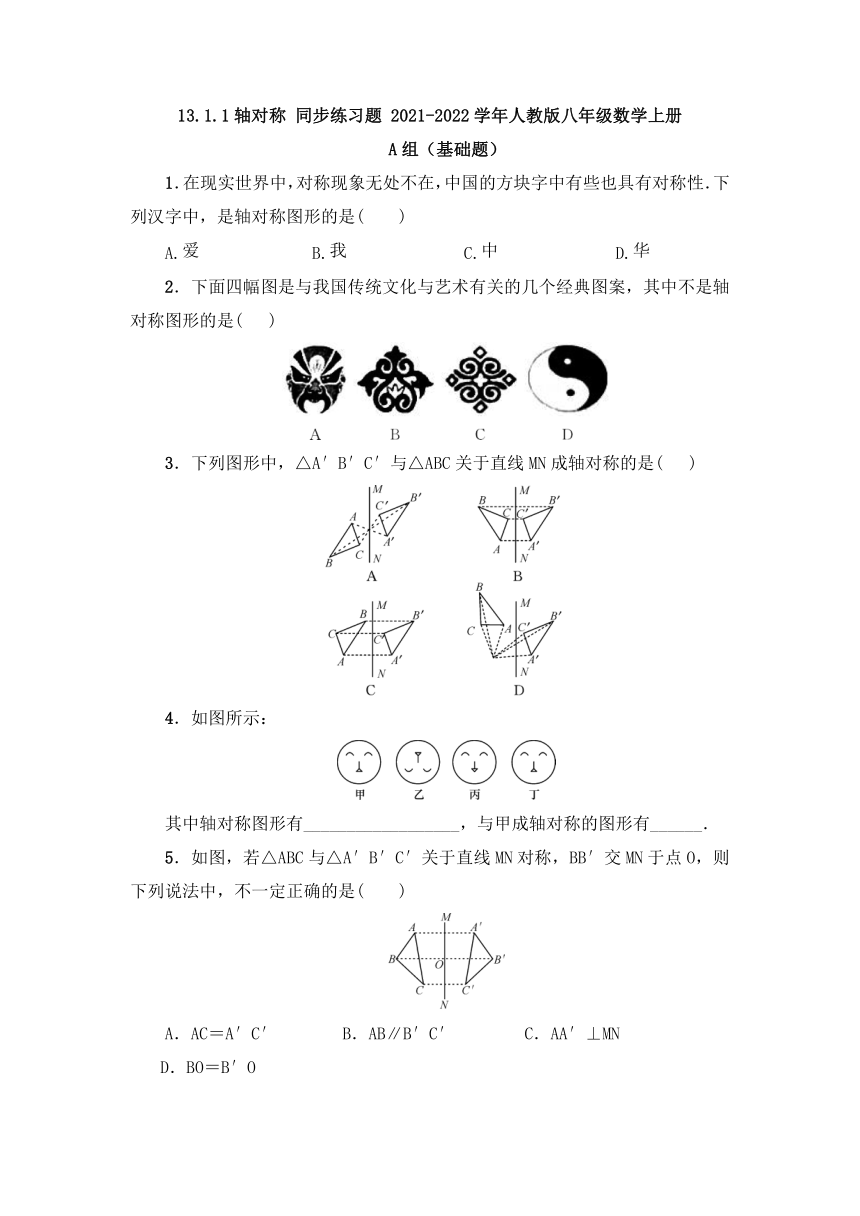 | |
| 格式 | docx | ||
| 文件大小 | 186.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-03 11:45:07 | ||
图片预览




文档简介
13.1.1轴对称
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.在现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是轴对称图形的是(
)
A.
B.
C.
D.
2.下面四幅图是与我国传统文化与艺术有关的几个经典图案,其中不是轴对称图形的是(
)
3.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是(
)
4.如图所示:
其中轴对称图形有__________________,与甲成轴对称的图形有______.
5.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中,不一定正确的是(
)
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+∠DCF=150°,则∠AFE+∠BCD=(
)
A.150°
B.300°
C.210°
D.330°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为(
)
A.10°
B.20°
C.30°
D.40°
8.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
9.如图,序号①②③④对应的三角形都是△ABC进行了一次变换之后得到的,其中是通过轴对称得到的是(
)
A.①
B.②
C.③
D.④
B组(中档题)
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,则下列说法错误的是(
)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
11.下列说法:①关于某条直线对称的两个三角形一定全等;②轴对称图形至少有一条对称轴;③全等三角形一定能关于某条直线对称;④轴对称图形的对称轴是对称点所连线段的垂直平分线;⑤如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.其中错误的是______.(填序号)
12.如图,已知AD所在直线是△ABC的对称轴,点E,F是AD上的两点.若BC=4,AD=3,则图中阴影部分的面积是______.
13.如图,阴影部分的面积为8
cm2,则正方形ABCD的边长为______cm.
14.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的线段和角;
(3)图中还有对称的三角形吗?
15.如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F.若△PEF的周长等于20
cm,求MN的长.
C组(综合题)
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
参考答案
13.1.1轴对称
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.在现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是轴对称图形的是(C)
A.
B.
C.
D.
2.下面四幅图是与我国传统文化与艺术有关的几个经典图案,其中不是轴对称图形的是(D)
3.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是(B)
4.如图所示:
其中轴对称图形有甲、乙、丙、丁,与甲成轴对称的图形有丁.
5.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中,不一定正确的是(B)
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+∠DCF=150°,则∠AFE+∠BCD=(B)
A.150°
B.300°
C.210°
D.330°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为(A)
A.10°
B.20°
C.30°
D.40°
8.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG.
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,AB=EF,BC=EH.
∴∠G=360°-∠H-∠E-∠F=55°,a=5
cm,b=4
cm.
9.如图,序号①②③④对应的三角形都是△ABC进行了一次变换之后得到的,其中是通过轴对称得到的是(A)
A.①
B.②
C.③
D.④
B组(中档题)
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,则下列说法错误的是(B)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
11.下列说法:①关于某条直线对称的两个三角形一定全等;②轴对称图形至少有一条对称轴;③全等三角形一定能关于某条直线对称;④轴对称图形的对称轴是对称点所连线段的垂直平分线;⑤如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.其中错误的是③⑤.(填序号)
12.如图,已知AD所在直线是△ABC的对称轴,点E,F是AD上的两点.若BC=4,AD=3,则图中阴影部分的面积是3.
13.如图,阴影部分的面积为8
cm2,则正方形ABCD的边长为4cm.
14.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的线段和角;
(3)图中还有对称的三角形吗?
解:(1)点A与点A,点B与点D,点C与点E.
(2)AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,∠C=∠E.
(3)△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
15.如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F.若△PEF的周长等于20
cm,求MN的长.
解:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,PF=NF.
又∵△PEF的周长为20
cm,
即PE+EF+PF=20
cm,
∴ME+EF+FN=20
cm,
即MN=20
cm.
C组(综合题)
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:(1)证明:∵四边形ABCD是长方形,
∴AD=BC,∠A=∠D=∠B=∠DCB=90°.
根据折叠的性质得:GC=AD,∠G=∠D=∠GCE=∠A=90°.
∴GC=BC,∠G=∠B.
∵∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,
∴∠GCF=∠BCE.
∴△FGC≌△EBC(ASA).
(2)由折叠性质得:S四边形ECGF=S四边形EADF.
∵△FGC≌△EBC,∴S△FGC=S△EBC.
∴S四边形ECGF=S四边形EFCB.
∴S四边形EADF=S四边形EFCB=S长方形ABCD.
∵AB=8,AD=4,
∴S长方形ABCD=8×4=32.
∴S四边形ECGF=16.
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.在现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是轴对称图形的是(
)
A.
B.
C.
D.
2.下面四幅图是与我国传统文化与艺术有关的几个经典图案,其中不是轴对称图形的是(
)
3.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是(
)
4.如图所示:
其中轴对称图形有__________________,与甲成轴对称的图形有______.
5.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中,不一定正确的是(
)
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+∠DCF=150°,则∠AFE+∠BCD=(
)
A.150°
B.300°
C.210°
D.330°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为(
)
A.10°
B.20°
C.30°
D.40°
8.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
9.如图,序号①②③④对应的三角形都是△ABC进行了一次变换之后得到的,其中是通过轴对称得到的是(
)
A.①
B.②
C.③
D.④
B组(中档题)
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,则下列说法错误的是(
)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
11.下列说法:①关于某条直线对称的两个三角形一定全等;②轴对称图形至少有一条对称轴;③全等三角形一定能关于某条直线对称;④轴对称图形的对称轴是对称点所连线段的垂直平分线;⑤如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.其中错误的是______.(填序号)
12.如图,已知AD所在直线是△ABC的对称轴,点E,F是AD上的两点.若BC=4,AD=3,则图中阴影部分的面积是______.
13.如图,阴影部分的面积为8
cm2,则正方形ABCD的边长为______cm.
14.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的线段和角;
(3)图中还有对称的三角形吗?
15.如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F.若△PEF的周长等于20
cm,求MN的长.
C组(综合题)
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
参考答案
13.1.1轴对称
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.在现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性.下列汉字中,是轴对称图形的是(C)
A.
B.
C.
D.
2.下面四幅图是与我国传统文化与艺术有关的几个经典图案,其中不是轴对称图形的是(D)
3.下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是(B)
4.如图所示:
其中轴对称图形有甲、乙、丙、丁,与甲成轴对称的图形有丁.
5.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法中,不一定正确的是(B)
A.AC=A′C′
B.AB∥B′C′
C.AA′⊥MN
D.BO=B′O
6.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴.若∠AFC+∠DCF=150°,则∠AFE+∠BCD=(B)
A.150°
B.300°
C.210°
D.330°
7.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为(A)
A.10°
B.20°
C.30°
D.40°
8.如图,两个四边形关于直线l对称,∠C=90°,试写出a,b的长度,并求出∠G的度数.
解:∵两个四边形关于直线l对称,
∴四边形ABCD≌四边形FEHG.
∴∠H=∠C=90°,∠A=∠F=80°,∠E=∠B=135°,AB=EF,BC=EH.
∴∠G=360°-∠H-∠E-∠F=55°,a=5
cm,b=4
cm.
9.如图,序号①②③④对应的三角形都是△ABC进行了一次变换之后得到的,其中是通过轴对称得到的是(A)
A.①
B.②
C.③
D.④
B组(中档题)
10.如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,则下列说法错误的是(B)
A.AM=BM
B.AP=BN
C.∠MAP=∠MBP
D.∠ANM=∠BNM
11.下列说法:①关于某条直线对称的两个三角形一定全等;②轴对称图形至少有一条对称轴;③全等三角形一定能关于某条直线对称;④轴对称图形的对称轴是对称点所连线段的垂直平分线;⑤如果图形甲和图形乙关于直线MN对称,则图形甲是轴对称图形.其中错误的是③⑤.(填序号)
12.如图,已知AD所在直线是△ABC的对称轴,点E,F是AD上的两点.若BC=4,AD=3,则图中阴影部分的面积是3.
13.如图,阴影部分的面积为8
cm2,则正方形ABCD的边长为4cm.
14.如图,△ABC与△ADE关于直线MN对称,BC与DE的交点F在直线MN上.
(1)指出两个三角形中的对称点;
(2)指出两个三角形中相等的线段和角;
(3)图中还有对称的三角形吗?
解:(1)点A与点A,点B与点D,点C与点E.
(2)AB=AD,AC=AE,BC=DE,∠BAC=∠DAE,∠B=∠D,∠C=∠E.
(3)△AFC与△AFE,△ABF与△ADF,也都关于直线MN成轴对称.
15.如图,点P在∠AOB内,M,N分别是点P关于AO,BO的对称点,MN分别交AO,BO于点E,F.若△PEF的周长等于20
cm,求MN的长.
解:∵M,N分别是点P关于AO,BO的对称点,
∴ME=PE,PF=NF.
又∵△PEF的周长为20
cm,
即PE+EF+PF=20
cm,
∴ME+EF+FN=20
cm,
即MN=20
cm.
C组(综合题)
16.如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)求证:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
解:(1)证明:∵四边形ABCD是长方形,
∴AD=BC,∠A=∠D=∠B=∠DCB=90°.
根据折叠的性质得:GC=AD,∠G=∠D=∠GCE=∠A=90°.
∴GC=BC,∠G=∠B.
∵∠GCF+∠ECF=90°,∠BCE+∠ECF=90°,
∴∠GCF=∠BCE.
∴△FGC≌△EBC(ASA).
(2)由折叠性质得:S四边形ECGF=S四边形EADF.
∵△FGC≌△EBC,∴S△FGC=S△EBC.
∴S四边形ECGF=S四边形EFCB.
∴S四边形EADF=S四边形EFCB=S长方形ABCD.
∵AB=8,AD=4,
∴S长方形ABCD=8×4=32.
∴S四边形ECGF=16.
