安徽省怀宁县高河中学2011-2012学年高二下学期第三次月考数学(文)试题(无答案)
文档属性
| 名称 | 安徽省怀宁县高河中学2011-2012学年高二下学期第三次月考数学(文)试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 123.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-18 19:18:49 | ||
图片预览

文档简介
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1. 下列命题中的假命题是( )
A. B. C. D.
2. 顶点在原点,焦点在x轴上且过点的抛物线的标准方程是( )
A. B. C. D.
3. 若一个命题p的逆命题是一个真命题,则下列判断一定正确的是
A.命题p是真命题 B.命题p的逆否命题是真命题
C.命题p的否定是真命题 D.命题p的否命题是真命题
4. “a>0”是“a >0”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
5. 曲线y=-x3+3x 在点A(1,2)处的切线方程为( )
A.y=-3x+5 B.y=3x-1 C.y=3x+5 D.y=2
6. 已知椭圆,若其焦点在轴上且焦距为,则等于( )
A. B.-4 C. 16 D.
7.若双曲线的离心率为2,则等于( )
A. 2 B. C. D. 1
8 .在复平面内,复数所对应的点位于( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
x 0 1 2 3
y 1 3 5 7
9.已知x与y之间的一组数据:
则y与x的线性回归方程为必过点 ( )
A.(2,2) B.(1,2) C.(1.5,0) D.(1.5,4)
10.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
根据表中数据得到5.059,因为p(K≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
A.97.5% B.95% C.90% D.无充分根据
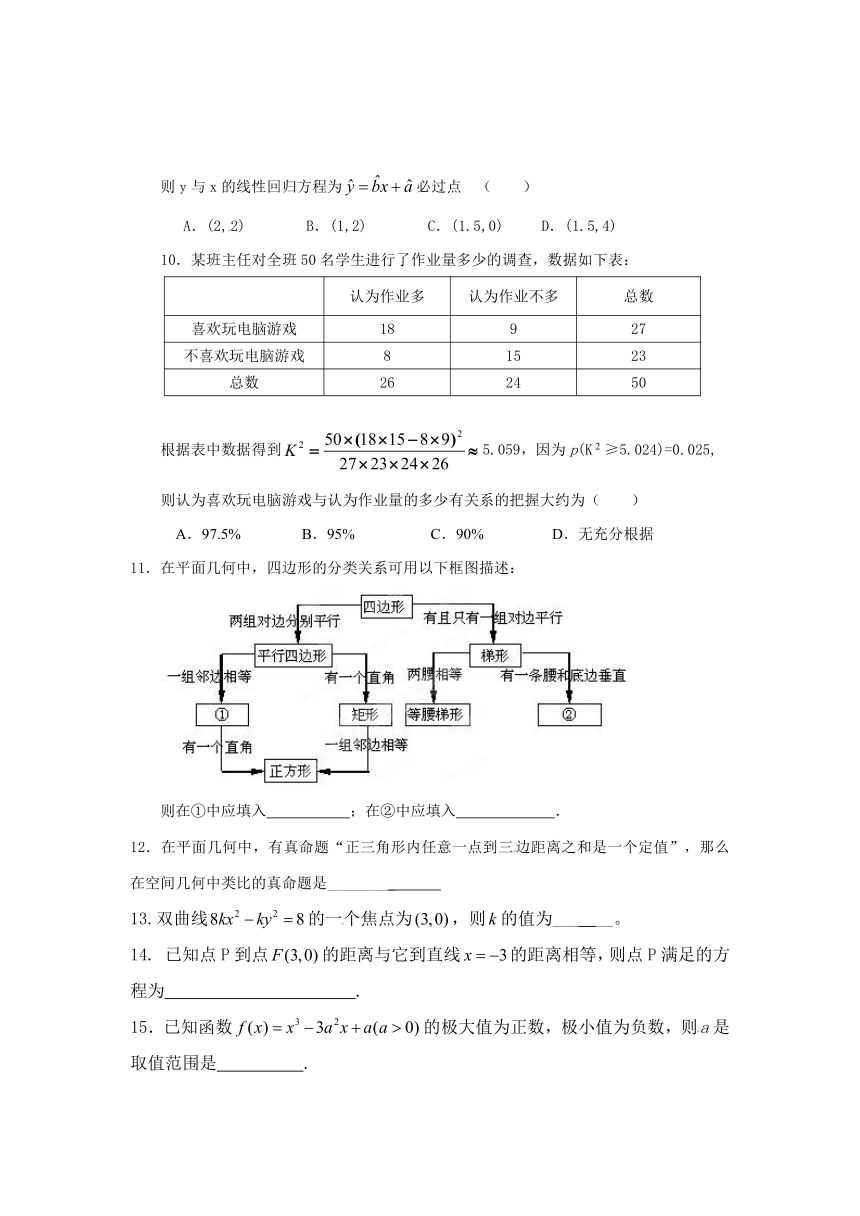
11.在平面几何中,四边形的分类关系可用以下框图描述:
则在①中应填入 ;在②中应填入 .
12.在平面几何中,有真命题“正三角形内任意一点到三边距离之和是一个定值”,那么在空间几何中类比的真命题是_________
13.双曲线的一个焦点为,则的值为___ __。
14. 已知点P到点的距离与它到直线的距离相等,则点P满足的方程为 .
15.已知函数的极大值为正数,极小值为负数,则a是取值范围是 .
三、解答题:本大题共6小题,共75分。解答应写出必要的文字说明、证明过程或演算步骤。
16. (本小题满分12分)已知命题p:m>4,;命题q:方程4x +4(m-2)x+9=0有实根.若为真,求实数m的取值范围.
17.(本小题满分12分)已知函数,求的极大值和极小值.
18. (本题满分13分)在平面直角坐标系O中,过点T(3,0)且斜率为1的直线与抛物线=2相交于A、B两点.求的值.
19.(用分析法证明)(12分)求证:。
20.(本小题满分14分)一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成,如图所示.
(1)建立适当的直角坐标系,求隧道上半部分所在椭圆的标准方程;
(2)一辆卡车运载一个长方形的集装箱,此箱平放在车上与车同宽,车与箱的高度共计4.2米,箱宽3米,若要求通过隧道时,车体不得超过中线.试问这辆卡车是否能通过此隧道,请说明理由.
21. (本题满分12分)
如图所示,F1、F2分别为椭圆C:的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点P到F1、F2两点的距离之和为4.
(1)求椭圆C的方程;
(2)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.
1. 下列命题中的假命题是( )
A. B. C. D.
2. 顶点在原点,焦点在x轴上且过点的抛物线的标准方程是( )
A. B. C. D.
3. 若一个命题p的逆命题是一个真命题,则下列判断一定正确的是
A.命题p是真命题 B.命题p的逆否命题是真命题
C.命题p的否定是真命题 D.命题p的否命题是真命题
4. “a>0”是“a >0”的( )
A.充要条件 B.充分不必要条件
C.必要不充分条件 D.既不充分也不必要条件
5. 曲线y=-x3+3x 在点A(1,2)处的切线方程为( )
A.y=-3x+5 B.y=3x-1 C.y=3x+5 D.y=2
6. 已知椭圆,若其焦点在轴上且焦距为,则等于( )
A. B.-4 C. 16 D.
7.若双曲线的离心率为2,则等于( )
A. 2 B. C. D. 1
8 .在复平面内,复数所对应的点位于( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限
x 0 1 2 3
y 1 3 5 7
9.已知x与y之间的一组数据:
则y与x的线性回归方程为必过点 ( )
A.(2,2) B.(1,2) C.(1.5,0) D.(1.5,4)
10.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
认为作业多 认为作业不多 总数
喜欢玩电脑游戏 18 9 27
不喜欢玩电脑游戏 8 15 23
总数 26 24 50
根据表中数据得到5.059,因为p(K≥5.024)=0.025,
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为( )
A.97.5% B.95% C.90% D.无充分根据
11.在平面几何中,四边形的分类关系可用以下框图描述:
则在①中应填入 ;在②中应填入 .
12.在平面几何中,有真命题“正三角形内任意一点到三边距离之和是一个定值”,那么在空间几何中类比的真命题是_________
13.双曲线的一个焦点为,则的值为___ __。
14. 已知点P到点的距离与它到直线的距离相等,则点P满足的方程为 .
15.已知函数的极大值为正数,极小值为负数,则a是取值范围是 .
三、解答题:本大题共6小题,共75分。解答应写出必要的文字说明、证明过程或演算步骤。
16. (本小题满分12分)已知命题p:m>4,;命题q:方程4x +4(m-2)x+9=0有实根.若为真,求实数m的取值范围.
17.(本小题满分12分)已知函数,求的极大值和极小值.
18. (本题满分13分)在平面直角坐标系O中,过点T(3,0)且斜率为1的直线与抛物线=2相交于A、B两点.求的值.
19.(用分析法证明)(12分)求证:。
20.(本小题满分14分)一段双行道隧道的横截面边界由椭圆的上半部分和矩形的三边组成,如图所示.
(1)建立适当的直角坐标系,求隧道上半部分所在椭圆的标准方程;
(2)一辆卡车运载一个长方形的集装箱,此箱平放在车上与车同宽,车与箱的高度共计4.2米,箱宽3米,若要求通过隧道时,车体不得超过中线.试问这辆卡车是否能通过此隧道,请说明理由.
21. (本题满分12分)
如图所示,F1、F2分别为椭圆C:的左、右两个焦点,A、B为两个顶点,已知椭圆C上的点P到F1、F2两点的距离之和为4.
(1)求椭圆C的方程;
(2)过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点,求△F1PQ的面积.
同课章节目录
