浙教版科学2021-2022学年上学期九年级“培优提高”讲义(十九):杠杆(1)【word,含答案】
文档属性
| 名称 | 浙教版科学2021-2022学年上学期九年级“培优提高”讲义(十九):杠杆(1)【word,含答案】 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2021-09-02 11:56:51 | ||
图片预览


文档简介
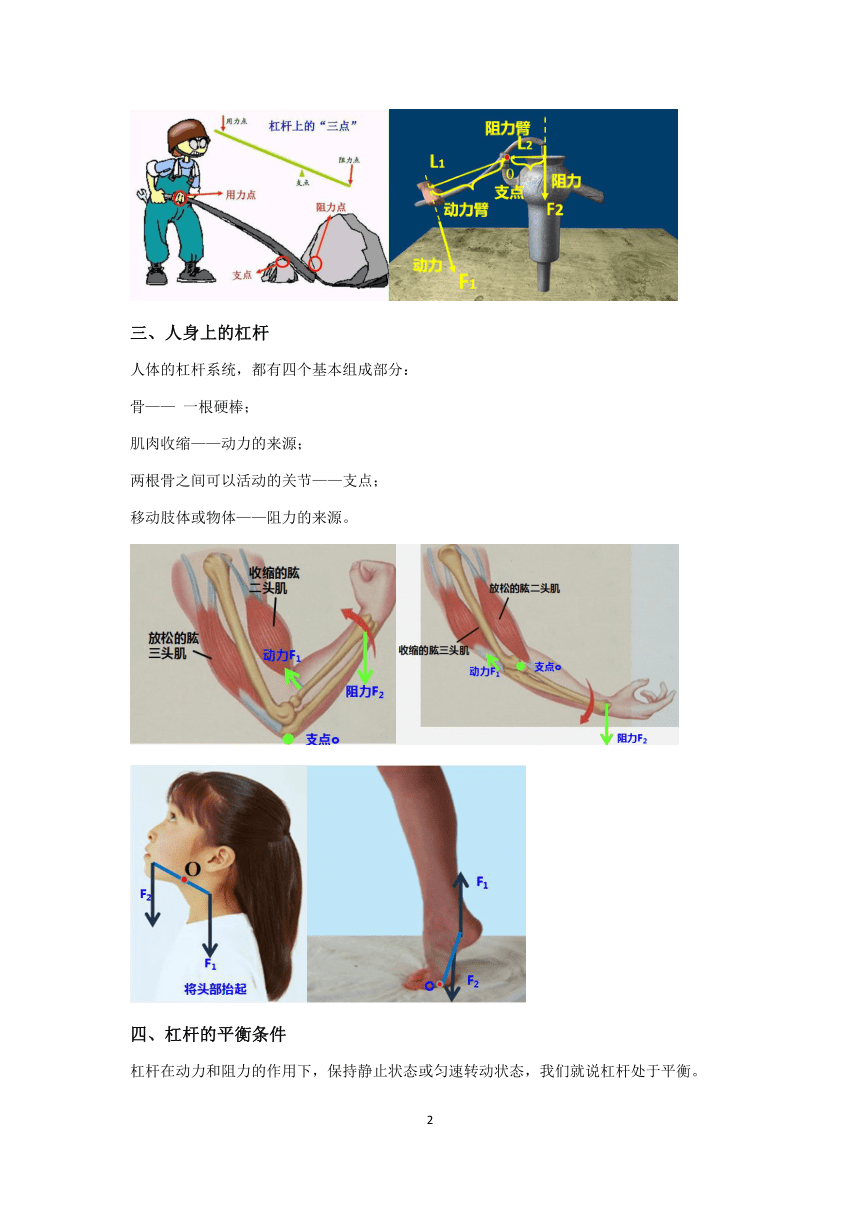
认识杠杆
①定义:在力的作用下能绕着固定点转动的硬棒就称为杠杆.
②注意:杠杆形状各异,可以是直的,也可以是弯的,但必须是硬棒。
杠杆五要素
支点
、动力、动力臂、阻力、阻力臂。
(1)支点:杠杆绕着转动的固定点O
叫做支点;
(2)动力:能够使杠杆转动的力F1
叫做动力;
(3)阻力:阻碍杠杆转动的力F2
叫做阻力;
(4)动力臂:从支点到动力作用线的距离L1
叫做动力臂;
(5)阻力臂:从支点到阻力作用线的距离L2
叫做阻力臂。
(6)力的作用线:过力的作用点,沿力的方向的直线。
“画力臂”可以用简单的顺口溜记住:一找点,二画线,三是作出垂线段。
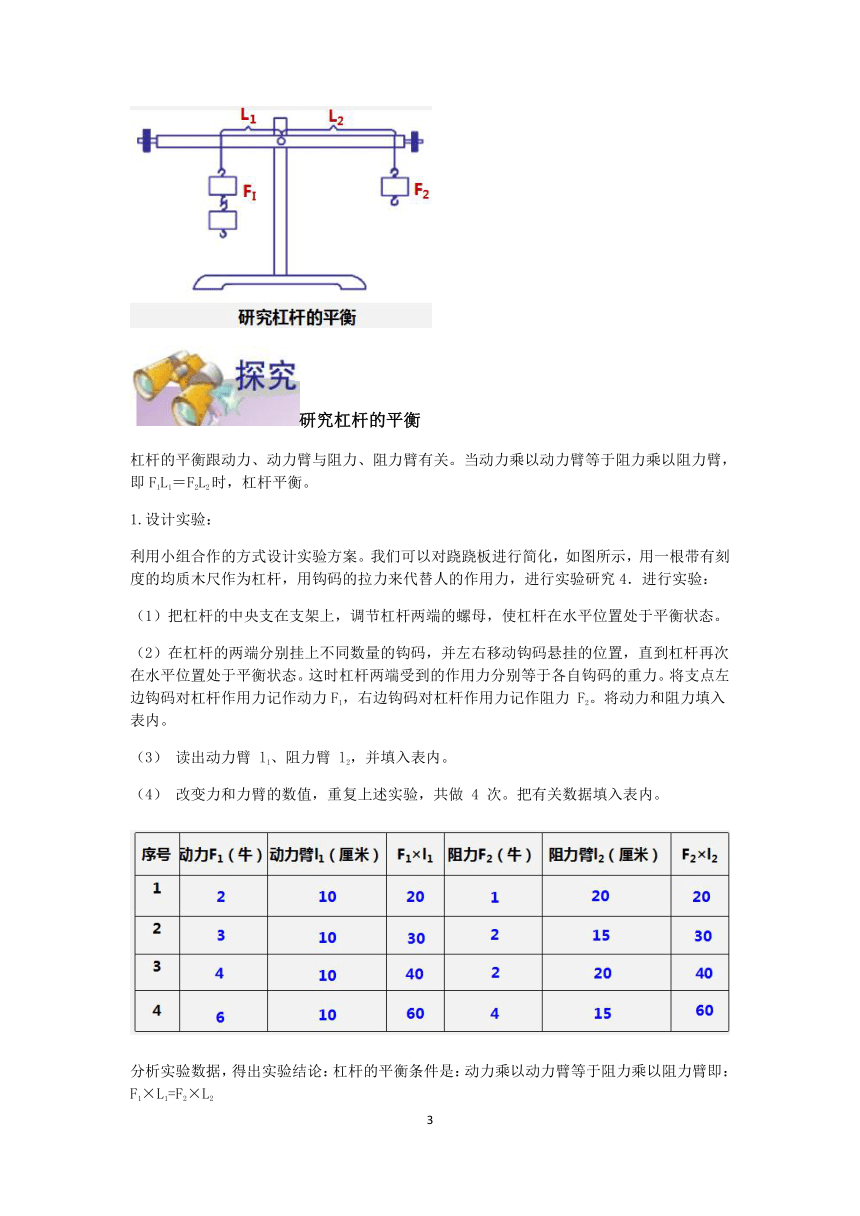
三、人身上的杠杆
人体的杠杆系统,都有四个基本组成部分:
骨——
一根硬棒;
肌肉收缩——动力的来源;
两根骨之间可以活动的关节——支点;
移动肢体或物体——阻力的来源。
四、杠杆的平衡条件
杠杆在动力和阻力的作用下,保持静止状态或匀速转动状态,我们就说杠杆处于平衡。
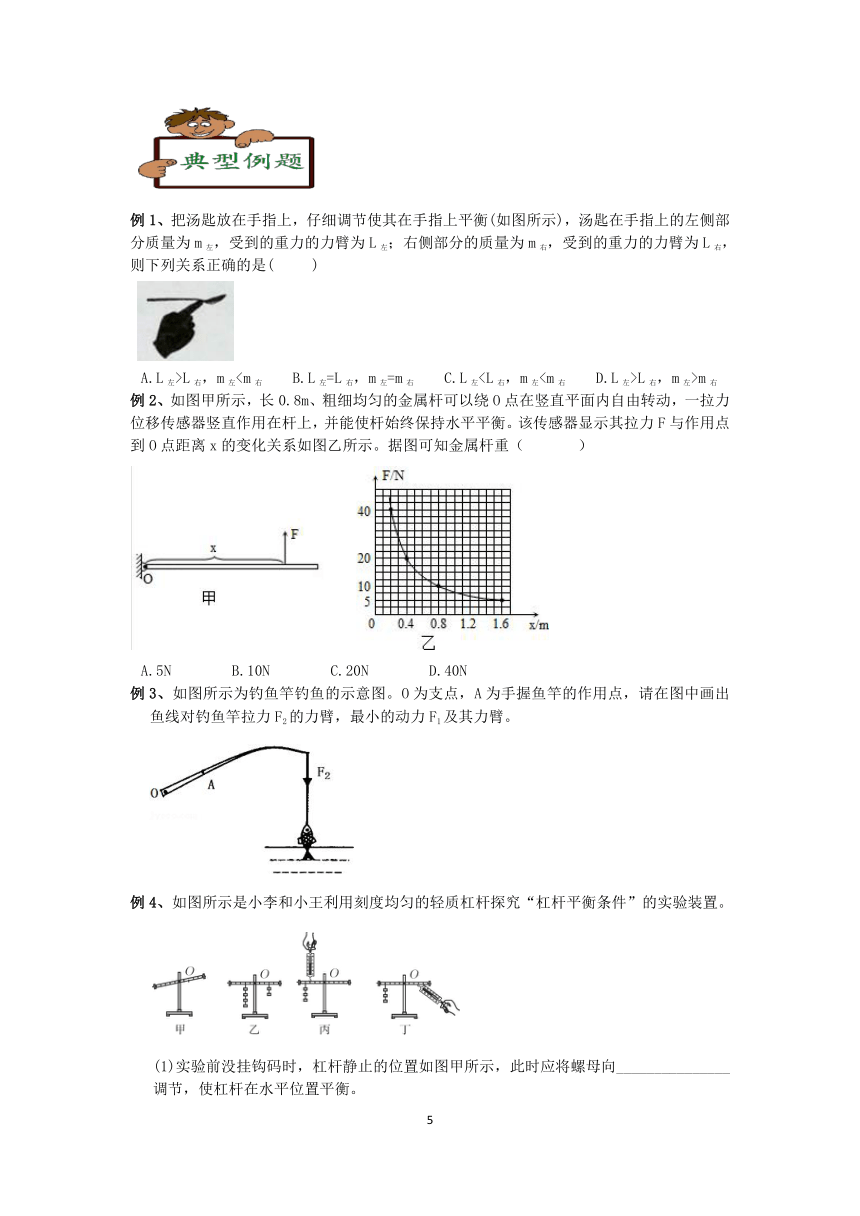
研究杠杆的平衡
杠杆的平衡跟动力、动力臂与阻力、阻力臂有关。当动力乘以动力臂等于阻力乘以阻力臂,即F1L1=F2L2时,杠杆平衡。
1.设计实验:
利用小组合作的方式设计实验方案。我们可以对跷跷板进行简化,如图所示,用一根带有刻度的均质木尺作为杠杆,用钩码的拉力来代替人的作用力,进行实验研究4.进行实验:
(1)把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态。
(2)在杠杆的两端分别挂上不同数量的钩码,并左右移动钩码悬挂的位置,直到杠杆再次在水平位置处于平衡状态。这时杠杆两端受到的作用力分别等于各自钩码的重力。将支点左边钩码对杠杆作用力记作动力F1,右边钩码对杠杆作用力记作阻力
F2。将动力和阻力填入表内。
(3)
读出动力臂
l1、阻力臂
l2,并填入表内。
(4)
改变力和力臂的数值,重复上述实验,共做
4
次。把有关数据填入表内。
分析实验数据,得出实验结论:杠杆的平衡条件是:动力乘以动力臂等于阻力乘以阻力臂即:F1×L1=F2×L2
为什么要调节杠杆在水平位置平衡,而不使它处于倾斜状态平衡。
避免杠杆自重对杠杆平衡的影响,便于测量力臂。
2、杠杆调平的方法是什么?
左边高向左调,右边高向右调。
五、杠杆的分类
例1、把汤匙放在手指上,仔细调节使其在手指上平衡(如图所示),汤匙在手指上的左侧部分质量为m左,受到的重力的力臂为L左;右侧部分的质量为m右,受到的重力的力臂为L右,则下列关系正确的是(??
)
A.L左>L右,m左C.L左L右,m左>m右
例2、如图甲所示,长0.8m、粗细均匀的金属杆可以绕O点在竖直平面内自由转动,一拉力位移传感器竖直作用在杆上,并能使杆始终保持水平平衡。该传感器显示其拉力F与作用点到O点距离x的变化关系如图乙所示。据图可知金属杆重(
???)
A.5N????B.10N????C.20N????D.40N
例3、如图所示为钓鱼竿钓鱼的示意图。O为支点,A为手握鱼竿的作用点,请在图中画出鱼线对钓鱼竿拉力F2的力臂,最小的动力F1及其力臂。
例4、如图所示是小李和小王利用刻度均匀的轻质杠杆探究“杠杆平衡条件”的实验装置。
(1)实验前没挂钩码时,杠杆静止的位置如图甲所示,此时应将螺母向_______________调节,使杠杆在水平位置平衡。
(2)杠杆平衡后,小李在左右两侧分别挂上钩码,如图乙所示,杠杆的____________端会下沉,要使杠杆重新在水平位置平衡,在不改变钩码悬挂点的位置和改变较少钩码的前提下,只需将__________即可。
(3)小李和小王又分别设计了两种实验方案,小李的方案如图丙所示,小王的方案如图丁所示。你认为__________的实验方案更好,请说明你的理由:________________________。
(4)实验中小王发现:如果在杠杆的O点用弹簧测力计施加一个向上的力,这个力在探究实验时是否影响到杠杆的平衡?请说明理由:____________________________。
例5、图甲是一种壶口处配有自动开合小壶盖的电水壶。
(1)如图乙,电水壶底部的导线连接装置有铜环①、铜环②和铜柱③。经测试发现:①、②之间是绝缘的,②、③之间常温下有十几欧姆的电阻。则与水壶金属外壳相连的装置是__
__。
(2)图丙是自动开合小壶盖简化侧视图。OA是小壶盖,C是其重力作用点。B是小壶盖的配重。OB是配重柄。AOB能绕固定点O
自由转动。请在图丙中作出小壶盖的重力G及其力臂l。
(3)已知:小壶盖质量为4g,OA=3cm,OC=1.4cm,OB=1cm,∠AOB=135°。要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计,取1.4)
1.如图杠杆在水平位置处于平衡状态,下列等式能正确表示杠杆平衡条件的是(??
)
A.F?OC=G?OB?????B.F?AC=G?OB????C.F?OA=G?OB?????D.F?AD=G?AB
2.衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是(???
)
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
3.一根轻质木杆,A端细线下所挂50N的重物静止在水平地面上。当在B点加竖直向下的力F=30N作用时,木杆恰能在水平位置处于平衡状态,此时细线竖直。已知OA=15cm,OB=5cm,则重物对水平地面压力为(
)
A.80N????B.60N????C.40N????D.20N
4.材料相同的甲、乙两个物体分别挂在杠杆A、B两端,O为支点(OA<OB),如图所示,杠杆处于平衡状态.如果将甲、乙物体(不溶于水)浸没于水中,杠杆将会(???
)
A.A端下沉??B.B端下沉??C.仍保持平衡??D.无法确定
5.室内垃圾桶平时桶盖关闭,使垃圾散发的异味不会飘出,使用时用脚踩踏板,桶盖开启。根据室内垃圾桶的结构示意图可确定(??
)
A.桶中只有一个杠杆在起作用,且为省力杠杆
B.桶中只有一个杠杆在起作用,且为费力杠杆
C.桶中有两个杠杆在起作用,且都是省力杠杆
D.桶中有两个杠杆在起作用,一个是省力杠杆,一个是费力杠杆
6.如图是一种切甘蔗用的铡刀示意图。下列说法正确的是(??
)
A.刀刃很薄可以增大压力
B.铡刀实质上是一种费力杠杆
C.甘蔗放在a点比b点更易被切断
D.手沿F1方向用力比沿F2方向更省力
7.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面,则(??
)
A.F甲>F乙,因为甲方法的动力臂长
B.F甲<F乙,因为乙方法的阻力臂长
C.F甲>F乙,因为乙方法的阻力臂短
D.以上说法都不对
8.在“探究杠杆平衡条件”实验中,小科用一块T形板对实验装置进行改进。如图甲所示,T形板上有槽口ab和卡口cd,T形板通过槽口ab可以绕着杠杆的0点自由旋转并上下移动,弹簧测力计与一根质量可以忽略的碳素细棒MN相连,碳素细棒MN刚好卡入T形板的卡口cd,如图乙所示。
(1)小想认为要完成这个实验,还需要一把刻度尺,但小科认为只要在T形板上稍微进行改进,不添加器材也可完成实验。小科对T形板进行的改进方法是
________。
(2)利用这个装置进行实验的优点为:________。
(3)小科在实验过程中,保持阻力、阻力臂不变,在杠杆水平平衡时,测出每一组动力臂L1和动力F1的数据,并利用实验数据绘制了F1与L1的关系图像,如图丙所示。请根据图像推算,当L1为5cm时,F1为________N。
9.小亮同学设计了如图所示的装置进行实验,利用小量程弹簧称测金属的密度,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________?N。
(2)被测金属块密度:ρ=________?g/cm3。
1.小明在按压式订书机的N点施加压力,将订书针钉入M点下方的纸张中,能正确表示他使用该订书机时的杠杆示意图的是(??
)
A.B.?C.D.
2.在公园里的儿童乐园内,两个小孩坐在跷跷板上,恰好处于平衡,此时(???
)。
A.两个小孩的质量一定相等??
B.两个小孩的重力和他们各自的力臂的乘积一定相等
C.两个小孩到支点的距离一定相等D.两个小孩的重力一定相等
3.O为一根轻质杠杆的支点,OA=2m,OB=2.5m,A点处挂着重100N的物体。若在B点施加一个竖直方向的力,使杠杆在水平位置上保持静止,则这个力的大小和方向是(??
)
A.20N,竖直向上??B.20N,竖直向下???C.80N,竖直向上??D.80N,竖直向下
4.如图为吊车从图示位置向上起吊货物的工作示意图,利用伸缩撑杆可使吊臂绕O点缓慢转动,伸缩撑杆为圆弧状,伸缩时伸缩撑杆对吊臂的支持力始终与吊臂垂直。下列说法中正确的是(??
)
A.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力大小不变
B.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变小
C.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变大
D.吊臂是一个省力杠杆
5.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中(?
)
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确????B.只有②③正确???C.只有①②正确???D.只有③④正确
6.轻质杠杆每小格的长度相等,O为支点.在杠杆左侧挂一物体甲,若在杠杆右侧挂一物体乙,并在物体乙的下方拴接一个弹簧,如图17所示,当杠杆在水平位置时,整个装置处于平衡状态.已知物体乙的重力为600N,弹簧对物体乙的作用力为300N.下列说法正确的是(???
)
A.物体甲的重力不可能为450N????
?B.物体甲的重力可能为300N
C.物体乙受到弹簧的一定处于压缩状态??D.物体乙受到绳子的拉力可能为900N或300N
7.如图所示,用轻质材料制成的吊桥搭在河对岸。一个人从吊桥的左端匀速走到吊桥的右端,桥面始终是水平的,不计吊桥和绳的重力,人从吊桥左端出发时开始计时。则人在吊桥上行走过程中,吊桥右端所受地面支持力F与人行走时间t的关系图像是(??
)
A.?B.?C.?D.
8.图中AOB是可绕O点无摩擦转动的轻杆,A端挂重300N的物块,AO与OB长度之比为5:4.人始终沿竖直方向拉挂在B端的轻环。要使轻杆水平平衡,人应施加拉力为_________N,人要不被拉起,则人重至少为_________N.与水平平衡相比,当轻杆在图中虚线位置平衡时,人的拉力将_________(选填“变大”、“变小”或“不变”)。
9.小刚和小明等同学一起做“探究杠杆的平衡条件”的实验
(1)小刚将杠杆中点置于支架上,当杠杆静止时,发现杠杆的左端上翘,此时,他应将杠杆两端的平衡螺母向_________(选填“左”或“右”)调节,使杠杆在水平位置平衡。
(2)如图所示,若每个钩码重0.5N,且杠杆上每格相等,小明在杠杆左端图示位置处挂上3个钩码,为使杠杆在水平位置平衡,他在图中A处施加一个方向向上的力F1,此力大小至少为_________N。
(3)若推去力F1,改在杠杆右端B处施加一个方向向下的力F2(如图乙所示),仍使杠杆平衡,请在图乙中画出力F2的力臂。
10.某建筑工地,有一“塔吊”正在准备起吊一底面积为0.8m?、质量为2400kg的圆柱形重物;如图所示,A为塔吊的配重,OB为塔吊的起重臂,C为能在起重臂上移动的载重小车,载重小车下挂有滑轮组,OB=25m。当载重小车在B点时,能安全起吊重物的最大质量是1200kg。现在载重小车从距离O点为10m的载重臂上,准备起吊该圆柱形重物(不计挂钩、滑轮组和钢丝绳重及摩擦。g=10N/kg)。问:
(1)起吊后,当重物匀速上升时,载重小车下每段钢丝绳的拉力为多大?
(2)如果将重物匀速提升20m,则拉力做功多少?
(3)塔吊将重物从起吊点提升20m后,载重小车最多能向B点方向再平移多少米,才能保证安全工作?
参考答案
例1、A
例2、C
例3、
例4、(1)右
(2)左
左端的钩码去掉一个
(3)小李
弹簧测力计在图丙的力与杠杆垂直,力臂在杠杆上便于测量
(4)不影响,这个作用力在杠杆O点的力的力臂等于零
例5、(1)铜环①
(2)图见解析
(3)4g【解析】
(2)如答图所示。
(3)当配重柄水平时,可求配重B最小质量,
OD=×OC=×1.4cm=1cm,
根据F1l1=F2l2得,G1l1=G2l2,m1g×OD=m2g×OB,m2===4g,
当小壶盖水平时,可求配重B最大质量,
OE=×OB=×1cm≈0.71cm,
根据F1l1=F2l2得,G1l1′=G2′l2′,m1g×OC=m2′g×OE,m2′==≈7.89g,
则配重B的质量取值范围为4~7.89g。(最小值3.92g、3.96g、3.98g等,最大值7.8g、7.84g、7.9g、8g等均可)
1.A
2.B
3.C
4.C
5.D
6.C
7.D
8.(1)在T形板的槽口ab上标上刻度
(2)可以改变拉力方向,且方便测量出相应的力臂长度,使实验结论更加可靠(3)6
9.(1)1.8(2)3
1.A
2.B
3.C
4.B
5.A
6.D
7.B
8.375;375;不变。
9.(1)左;(2)2;(3)见下图。
【解析】(1)实验前调节杠杆在水平位置平衡,将平衡螺母向较高的一端调节。杠杆左端上翘,此时应将杠杆两端的平衡螺母向左调节;
(2)根据杠杆的平衡条件可知,当力臂最大时,力才最小,由图以A到O点距离为力臂是最大的力臂,则力方向应竖直向上,若杠杆上每格长为l,F1×3l=3×0.5N×4l,所以F1=2N;
(3)力臂是支点到力的作用线的距离。先延长力的作用线,再从O点作它的垂线,即F2的力臂,如图所示:
10.
(1)6000N
(2)4.8×105J
(3)2.5m
【解析】(1)由图知承重钢丝绳的股数为n=4,即重物匀速上升时,载重小车下每段钢丝绳的拉力;
(2)
拉力做功等于克服重力做功W=Gh=mgh=2400kg×10N/kg×20m=4.8×105J;
(3)
由于载重小车在B点时,能安全起吊重物的最大质量是1200kg,此时力与力臂的乘积为G'×OB=1200kg×10N/kg×25m,
当提升重物为2400kg时,最大力臂为Lm,则2400kg×10N/kg×Lm=1200kg×10N/kg×25m,
故最大力臂Lm=12.5m,
载重小车最多能向B点方向再平移12.5m-10m=2.5m。
2021-2022学年上学期浙教版科学九年级“培优提高”讲义(十九)
杠杆(1)
①定义:在力的作用下能绕着固定点转动的硬棒就称为杠杆.
②注意:杠杆形状各异,可以是直的,也可以是弯的,但必须是硬棒。
杠杆五要素
支点
、动力、动力臂、阻力、阻力臂。
(1)支点:杠杆绕着转动的固定点O
叫做支点;
(2)动力:能够使杠杆转动的力F1
叫做动力;
(3)阻力:阻碍杠杆转动的力F2
叫做阻力;
(4)动力臂:从支点到动力作用线的距离L1
叫做动力臂;
(5)阻力臂:从支点到阻力作用线的距离L2
叫做阻力臂。
(6)力的作用线:过力的作用点,沿力的方向的直线。
“画力臂”可以用简单的顺口溜记住:一找点,二画线,三是作出垂线段。
三、人身上的杠杆
人体的杠杆系统,都有四个基本组成部分:
骨——
一根硬棒;
肌肉收缩——动力的来源;
两根骨之间可以活动的关节——支点;
移动肢体或物体——阻力的来源。
四、杠杆的平衡条件
杠杆在动力和阻力的作用下,保持静止状态或匀速转动状态,我们就说杠杆处于平衡。
研究杠杆的平衡
杠杆的平衡跟动力、动力臂与阻力、阻力臂有关。当动力乘以动力臂等于阻力乘以阻力臂,即F1L1=F2L2时,杠杆平衡。
1.设计实验:
利用小组合作的方式设计实验方案。我们可以对跷跷板进行简化,如图所示,用一根带有刻度的均质木尺作为杠杆,用钩码的拉力来代替人的作用力,进行实验研究4.进行实验:
(1)把杠杆的中央支在支架上,调节杠杆两端的螺母,使杠杆在水平位置处于平衡状态。
(2)在杠杆的两端分别挂上不同数量的钩码,并左右移动钩码悬挂的位置,直到杠杆再次在水平位置处于平衡状态。这时杠杆两端受到的作用力分别等于各自钩码的重力。将支点左边钩码对杠杆作用力记作动力F1,右边钩码对杠杆作用力记作阻力
F2。将动力和阻力填入表内。
(3)
读出动力臂
l1、阻力臂
l2,并填入表内。
(4)
改变力和力臂的数值,重复上述实验,共做
4
次。把有关数据填入表内。
分析实验数据,得出实验结论:杠杆的平衡条件是:动力乘以动力臂等于阻力乘以阻力臂即:F1×L1=F2×L2
为什么要调节杠杆在水平位置平衡,而不使它处于倾斜状态平衡。
避免杠杆自重对杠杆平衡的影响,便于测量力臂。
2、杠杆调平的方法是什么?
左边高向左调,右边高向右调。
五、杠杆的分类
例1、把汤匙放在手指上,仔细调节使其在手指上平衡(如图所示),汤匙在手指上的左侧部分质量为m左,受到的重力的力臂为L左;右侧部分的质量为m右,受到的重力的力臂为L右,则下列关系正确的是(??
)
A.L左>L右,m左
例2、如图甲所示,长0.8m、粗细均匀的金属杆可以绕O点在竖直平面内自由转动,一拉力位移传感器竖直作用在杆上,并能使杆始终保持水平平衡。该传感器显示其拉力F与作用点到O点距离x的变化关系如图乙所示。据图可知金属杆重(
???)
A.5N????B.10N????C.20N????D.40N
例3、如图所示为钓鱼竿钓鱼的示意图。O为支点,A为手握鱼竿的作用点,请在图中画出鱼线对钓鱼竿拉力F2的力臂,最小的动力F1及其力臂。
例4、如图所示是小李和小王利用刻度均匀的轻质杠杆探究“杠杆平衡条件”的实验装置。
(1)实验前没挂钩码时,杠杆静止的位置如图甲所示,此时应将螺母向_______________调节,使杠杆在水平位置平衡。
(2)杠杆平衡后,小李在左右两侧分别挂上钩码,如图乙所示,杠杆的____________端会下沉,要使杠杆重新在水平位置平衡,在不改变钩码悬挂点的位置和改变较少钩码的前提下,只需将__________即可。
(3)小李和小王又分别设计了两种实验方案,小李的方案如图丙所示,小王的方案如图丁所示。你认为__________的实验方案更好,请说明你的理由:________________________。
(4)实验中小王发现:如果在杠杆的O点用弹簧测力计施加一个向上的力,这个力在探究实验时是否影响到杠杆的平衡?请说明理由:____________________________。
例5、图甲是一种壶口处配有自动开合小壶盖的电水壶。
(1)如图乙,电水壶底部的导线连接装置有铜环①、铜环②和铜柱③。经测试发现:①、②之间是绝缘的,②、③之间常温下有十几欧姆的电阻。则与水壶金属外壳相连的装置是__
__。
(2)图丙是自动开合小壶盖简化侧视图。OA是小壶盖,C是其重力作用点。B是小壶盖的配重。OB是配重柄。AOB能绕固定点O
自由转动。请在图丙中作出小壶盖的重力G及其力臂l。
(3)已知:小壶盖质量为4g,OA=3cm,OC=1.4cm,OB=1cm,∠AOB=135°。要求倒水时,壶身最多倾斜45°,小壶盖便自动打开;壶身竖直时,小壶盖在水平位置自动闭合。求配重B的质量取值范围。(配重柄质量和O点的摩擦均忽略不计,取1.4)
1.如图杠杆在水平位置处于平衡状态,下列等式能正确表示杠杆平衡条件的是(??
)
A.F?OC=G?OB?????B.F?AC=G?OB????C.F?OA=G?OB?????D.F?AD=G?AB
2.衣服夹是一种常用物品,如图所示,给出了用手捏开和夹住物品时的两种情况。下列说法中,正确的是(???
)
A.当用手将其捏开时,它是费力杠杆
B.当用其夹住物品时,它是费力杠杆
C.无论用手将其捏开还是夹住物品时,它都是费力杠杆
D.无论用手将其捏开还是夹住物品时,它都是省力杠杆
3.一根轻质木杆,A端细线下所挂50N的重物静止在水平地面上。当在B点加竖直向下的力F=30N作用时,木杆恰能在水平位置处于平衡状态,此时细线竖直。已知OA=15cm,OB=5cm,则重物对水平地面压力为(
)
A.80N????B.60N????C.40N????D.20N
4.材料相同的甲、乙两个物体分别挂在杠杆A、B两端,O为支点(OA<OB),如图所示,杠杆处于平衡状态.如果将甲、乙物体(不溶于水)浸没于水中,杠杆将会(???
)
A.A端下沉??B.B端下沉??C.仍保持平衡??D.无法确定
5.室内垃圾桶平时桶盖关闭,使垃圾散发的异味不会飘出,使用时用脚踩踏板,桶盖开启。根据室内垃圾桶的结构示意图可确定(??
)
A.桶中只有一个杠杆在起作用,且为省力杠杆
B.桶中只有一个杠杆在起作用,且为费力杠杆
C.桶中有两个杠杆在起作用,且都是省力杠杆
D.桶中有两个杠杆在起作用,一个是省力杠杆,一个是费力杠杆
6.如图是一种切甘蔗用的铡刀示意图。下列说法正确的是(??
)
A.刀刃很薄可以增大压力
B.铡刀实质上是一种费力杠杆
C.甘蔗放在a点比b点更易被切断
D.手沿F1方向用力比沿F2方向更省力
7.如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面,则(??
)
A.F甲>F乙,因为甲方法的动力臂长
B.F甲<F乙,因为乙方法的阻力臂长
C.F甲>F乙,因为乙方法的阻力臂短
D.以上说法都不对
8.在“探究杠杆平衡条件”实验中,小科用一块T形板对实验装置进行改进。如图甲所示,T形板上有槽口ab和卡口cd,T形板通过槽口ab可以绕着杠杆的0点自由旋转并上下移动,弹簧测力计与一根质量可以忽略的碳素细棒MN相连,碳素细棒MN刚好卡入T形板的卡口cd,如图乙所示。
(1)小想认为要完成这个实验,还需要一把刻度尺,但小科认为只要在T形板上稍微进行改进,不添加器材也可完成实验。小科对T形板进行的改进方法是
________。
(2)利用这个装置进行实验的优点为:________。
(3)小科在实验过程中,保持阻力、阻力臂不变,在杠杆水平平衡时,测出每一组动力臂L1和动力F1的数据,并利用实验数据绘制了F1与L1的关系图像,如图丙所示。请根据图像推算,当L1为5cm时,F1为________N。
9.小亮同学设计了如图所示的装置进行实验,利用小量程弹簧称测金属的密度,其中杠杆OAB支点为O(杠杆OAB质量不计),OA:OB=1:3。他实验的步骤如下:步骤一:用一细绳将体积为180cm3的金属块悬挂于A点,然后向容器中加水,使金属块浸没在水中。步骤二:使杠杆OAB在水平位置静止,读出弹簧测力计此时的读数为1.2N。
(1)金属块浸没在水中时受到的浮力为________?N。
(2)被测金属块密度:ρ=________?g/cm3。
1.小明在按压式订书机的N点施加压力,将订书针钉入M点下方的纸张中,能正确表示他使用该订书机时的杠杆示意图的是(??
)
A.B.?C.D.
2.在公园里的儿童乐园内,两个小孩坐在跷跷板上,恰好处于平衡,此时(???
)。
A.两个小孩的质量一定相等??
B.两个小孩的重力和他们各自的力臂的乘积一定相等
C.两个小孩到支点的距离一定相等D.两个小孩的重力一定相等
3.O为一根轻质杠杆的支点,OA=2m,OB=2.5m,A点处挂着重100N的物体。若在B点施加一个竖直方向的力,使杠杆在水平位置上保持静止,则这个力的大小和方向是(??
)
A.20N,竖直向上??B.20N,竖直向下???C.80N,竖直向上??D.80N,竖直向下
4.如图为吊车从图示位置向上起吊货物的工作示意图,利用伸缩撑杆可使吊臂绕O点缓慢转动,伸缩撑杆为圆弧状,伸缩时伸缩撑杆对吊臂的支持力始终与吊臂垂直。下列说法中正确的是(??
)
A.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力大小不变
B.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变小
C.匀速缓慢顶起吊臂的过程中,伸缩撑杆的支持力渐渐变大
D.吊臂是一个省力杠杆
5.一均匀木板AB,B端固定在墙壁的转轴上,木板可在竖直面内转动,木板下垫物块C,恰好使木板水平放置,如图所示.现在水平力F将C由B向匀速推动过程中,下列相关说法中(?
)
①物块C对木块AB的摩擦力方向向右
②木板AB仅受重力和物块C对它的支持力的作用
③物块C受到的重力和地面对它的支持力是一对平衡力
④推力F将逐渐变大
A.只有①④正确????B.只有②③正确???C.只有①②正确???D.只有③④正确
6.轻质杠杆每小格的长度相等,O为支点.在杠杆左侧挂一物体甲,若在杠杆右侧挂一物体乙,并在物体乙的下方拴接一个弹簧,如图17所示,当杠杆在水平位置时,整个装置处于平衡状态.已知物体乙的重力为600N,弹簧对物体乙的作用力为300N.下列说法正确的是(???
)
A.物体甲的重力不可能为450N????
?B.物体甲的重力可能为300N
C.物体乙受到弹簧的一定处于压缩状态??D.物体乙受到绳子的拉力可能为900N或300N
7.如图所示,用轻质材料制成的吊桥搭在河对岸。一个人从吊桥的左端匀速走到吊桥的右端,桥面始终是水平的,不计吊桥和绳的重力,人从吊桥左端出发时开始计时。则人在吊桥上行走过程中,吊桥右端所受地面支持力F与人行走时间t的关系图像是(??
)
A.?B.?C.?D.
8.图中AOB是可绕O点无摩擦转动的轻杆,A端挂重300N的物块,AO与OB长度之比为5:4.人始终沿竖直方向拉挂在B端的轻环。要使轻杆水平平衡,人应施加拉力为_________N,人要不被拉起,则人重至少为_________N.与水平平衡相比,当轻杆在图中虚线位置平衡时,人的拉力将_________(选填“变大”、“变小”或“不变”)。
9.小刚和小明等同学一起做“探究杠杆的平衡条件”的实验
(1)小刚将杠杆中点置于支架上,当杠杆静止时,发现杠杆的左端上翘,此时,他应将杠杆两端的平衡螺母向_________(选填“左”或“右”)调节,使杠杆在水平位置平衡。
(2)如图所示,若每个钩码重0.5N,且杠杆上每格相等,小明在杠杆左端图示位置处挂上3个钩码,为使杠杆在水平位置平衡,他在图中A处施加一个方向向上的力F1,此力大小至少为_________N。
(3)若推去力F1,改在杠杆右端B处施加一个方向向下的力F2(如图乙所示),仍使杠杆平衡,请在图乙中画出力F2的力臂。
10.某建筑工地,有一“塔吊”正在准备起吊一底面积为0.8m?、质量为2400kg的圆柱形重物;如图所示,A为塔吊的配重,OB为塔吊的起重臂,C为能在起重臂上移动的载重小车,载重小车下挂有滑轮组,OB=25m。当载重小车在B点时,能安全起吊重物的最大质量是1200kg。现在载重小车从距离O点为10m的载重臂上,准备起吊该圆柱形重物(不计挂钩、滑轮组和钢丝绳重及摩擦。g=10N/kg)。问:
(1)起吊后,当重物匀速上升时,载重小车下每段钢丝绳的拉力为多大?
(2)如果将重物匀速提升20m,则拉力做功多少?
(3)塔吊将重物从起吊点提升20m后,载重小车最多能向B点方向再平移多少米,才能保证安全工作?
参考答案
例1、A
例2、C
例3、
例4、(1)右
(2)左
左端的钩码去掉一个
(3)小李
弹簧测力计在图丙的力与杠杆垂直,力臂在杠杆上便于测量
(4)不影响,这个作用力在杠杆O点的力的力臂等于零
例5、(1)铜环①
(2)图见解析
(3)4g
(2)如答图所示。
(3)当配重柄水平时,可求配重B最小质量,
OD=×OC=×1.4cm=1cm,
根据F1l1=F2l2得,G1l1=G2l2,m1g×OD=m2g×OB,m2===4g,
当小壶盖水平时,可求配重B最大质量,
OE=×OB=×1cm≈0.71cm,
根据F1l1=F2l2得,G1l1′=G2′l2′,m1g×OC=m2′g×OE,m2′==≈7.89g,
则配重B的质量取值范围为4~7.89g。(最小值3.92g、3.96g、3.98g等,最大值7.8g、7.84g、7.9g、8g等均可)
1.A
2.B
3.C
4.C
5.D
6.C
7.D
8.(1)在T形板的槽口ab上标上刻度
(2)可以改变拉力方向,且方便测量出相应的力臂长度,使实验结论更加可靠(3)6
9.(1)1.8(2)3
1.A
2.B
3.C
4.B
5.A
6.D
7.B
8.375;375;不变。
9.(1)左;(2)2;(3)见下图。
【解析】(1)实验前调节杠杆在水平位置平衡,将平衡螺母向较高的一端调节。杠杆左端上翘,此时应将杠杆两端的平衡螺母向左调节;
(2)根据杠杆的平衡条件可知,当力臂最大时,力才最小,由图以A到O点距离为力臂是最大的力臂,则力方向应竖直向上,若杠杆上每格长为l,F1×3l=3×0.5N×4l,所以F1=2N;
(3)力臂是支点到力的作用线的距离。先延长力的作用线,再从O点作它的垂线,即F2的力臂,如图所示:
10.
(1)6000N
(2)4.8×105J
(3)2.5m
【解析】(1)由图知承重钢丝绳的股数为n=4,即重物匀速上升时,载重小车下每段钢丝绳的拉力;
(2)
拉力做功等于克服重力做功W=Gh=mgh=2400kg×10N/kg×20m=4.8×105J;
(3)
由于载重小车在B点时,能安全起吊重物的最大质量是1200kg,此时力与力臂的乘积为G'×OB=1200kg×10N/kg×25m,
当提升重物为2400kg时,最大力臂为Lm,则2400kg×10N/kg×Lm=1200kg×10N/kg×25m,
故最大力臂Lm=12.5m,
载重小车最多能向B点方向再平移12.5m-10m=2.5m。
2021-2022学年上学期浙教版科学九年级“培优提高”讲义(十九)
杠杆(1)
同课章节目录
- 第1章 物质及其变化
- 第1节 物质的变化
- 第2节 物质的酸碱性
- 第3节 常见的酸
- 第4节 常见的碱
- 第5节 酸和碱之间发生的反应
- 第6节 几种重要的盐
- 第2章 物质转化与材料利用
- 第1节 金属材料
- 第2节 金属的化学性质
- 第3节 有机物和有机合成材料
- 第4节 物质的分类
- 第5节 物质的转化
- 第6节 材料的利用与发展
- 第3章 能量的转化与守恒
- 第1节 能量及其形式
- 第2节 机械能
- 第3节 能量转化的量度
- 第4节 简单机械
- 第5节 物体的内能
- 第6节 电能
- 第7节 核能
- 第8节 能量的转化与守恒
- 第4章 代谢与平衡
- 第1节 食物与营养
- 第2节 食物的消化与吸收
- 第3节 体内物质的运输
- 第4节 能量的获得
- 第5节 体内物质的动态平衡
- 研究性学习课题
- 一 当地酸雨情况以及对农作物和建筑物的影响
- 二 金属对社会发展的作用
- 三 寻找自行车中的杠杆
- 四 怎样防治龋齿
