苏教版数学六年级上册 四 解决问题的策略课件(共25张PPT)
文档属性
| 名称 | 苏教版数学六年级上册 四 解决问题的策略课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 12:32:30 | ||
图片预览





文档简介
(共25张PPT)
2、解决问题的策略(2)
6
1个菠萝与(
)个桃一样重。
(1)
(2)
笔记本的单价是练习本的5倍。买4本笔记本的钱可以买(
)本练习本。
20
热热身
1、小明把720毫升果汁倒入9个同样容量的小杯里,正好都倒满,
?
720÷9=80(毫升)
答:每个小杯的容量是80毫升。
每个小杯的容量是多少毫升
先根据条件提出问题,再列式解答。
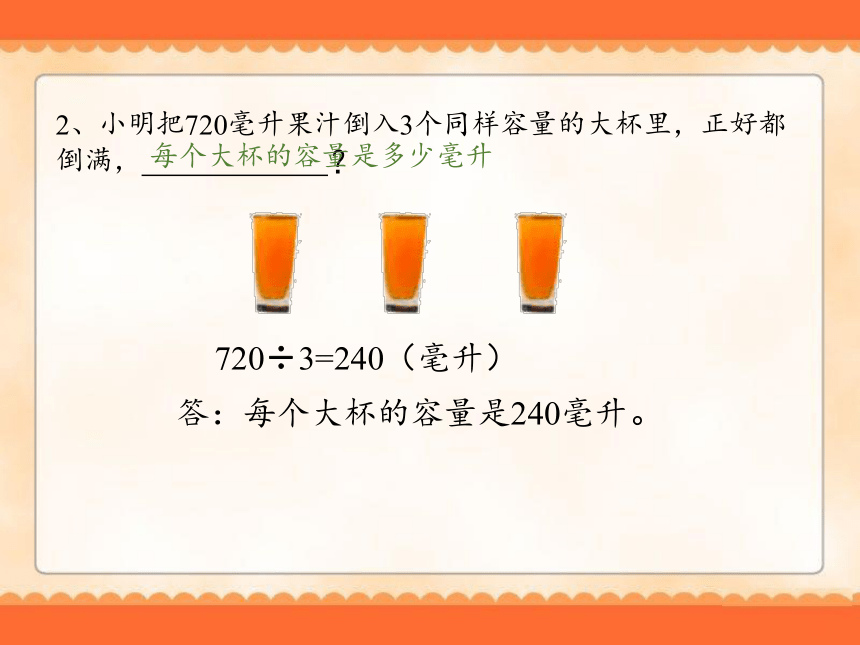
2、小明把720毫升果汁倒入3个同样容量的大杯里,正好都倒满,
?
720÷3=240(毫升)
答:每个大杯的容量是240毫升。
每个大杯的容量是多少毫升
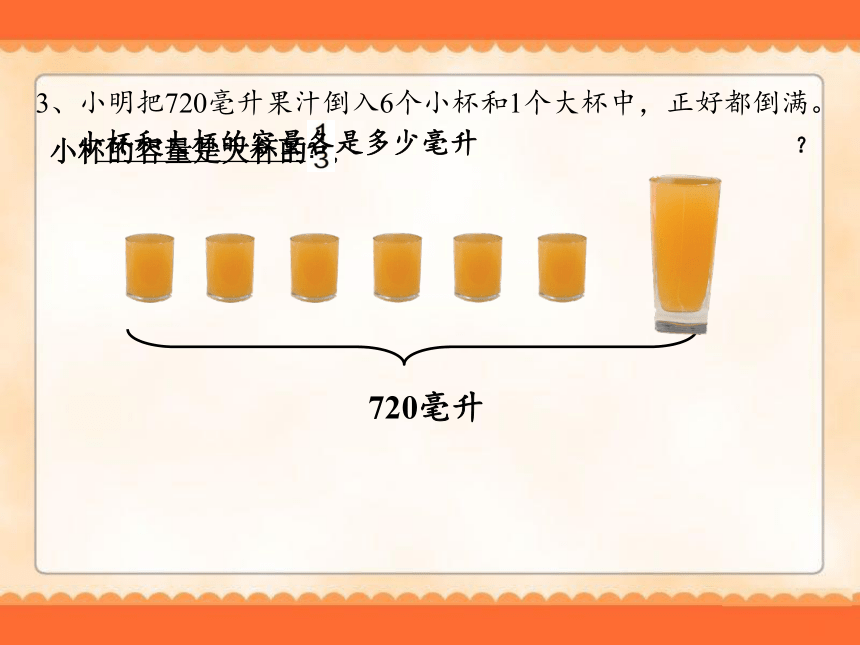
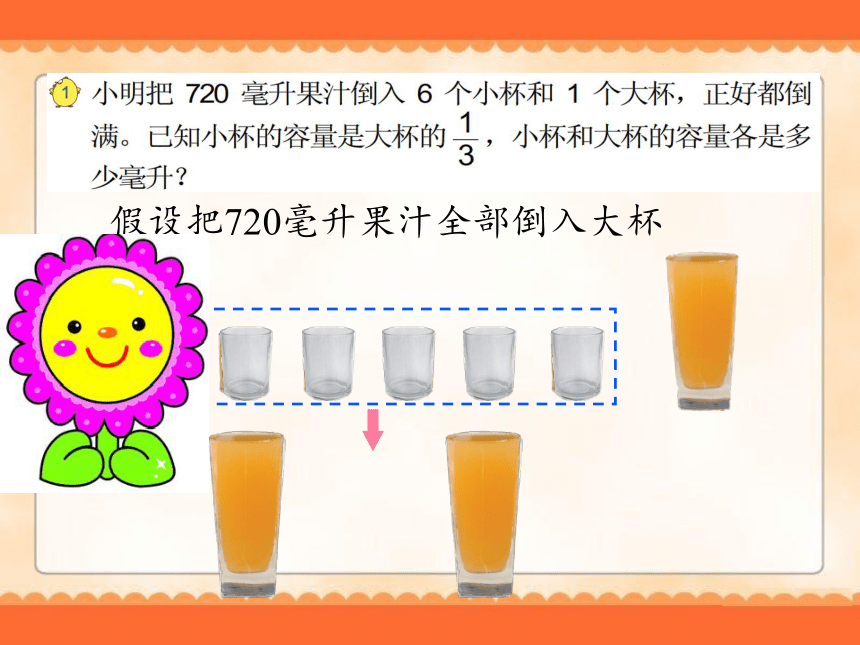
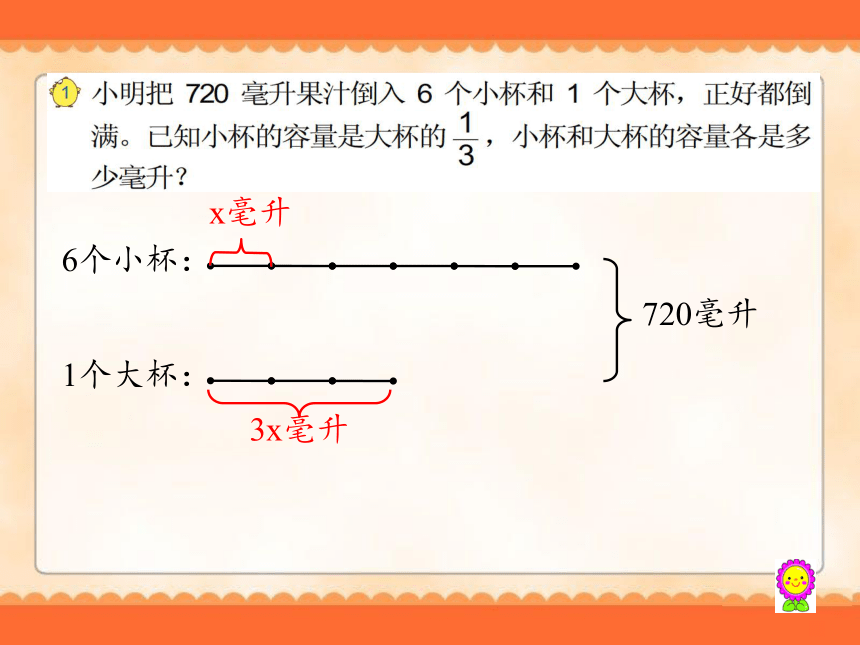
3、小明把720毫升果汁倒入6个小杯和1个大杯中,正好都倒满。
720毫升
小杯的容量是大杯的
,
小杯和大杯的容量各是多少毫升
?
?
6个小杯容量
+
1个大杯容量=
720毫升
1个大杯容量=
3个小杯容量
720毫升
假设把720毫升果汁全部倒入小杯
假设把720毫升果汁全部倒入大杯
6个小杯:
x毫升
3x毫升
1个大杯:
720毫升
选择一种方法列式解答,并进行检验。
假设把720毫升果汁
全部倒入小杯
小杯:1×3+6=9(杯)
大杯:
720÷9=80(毫升)
80×3=240(毫升)
720÷3=240(毫升)
240÷3
=
80
(毫升)
6÷3+1=3(杯)
假设把720毫升果汁
全部倒入大杯
大杯:
小杯:
列方程解答。
解:设小杯的容量是x毫升,则大杯容量是3x
毫升。
6个小杯的容量+1个大杯的容量=720毫升
大杯:80
×
3
=
240(毫升)
χ
=
720
÷
9
9χ
=
720
6χ
+
3χ
=
720
χ
=
80
检验:
★检验时要看我们所求答案是否符合题目中所有的条件。
1、看6个小杯和1个大杯的果汁是不是一共720毫升;
2、小杯的容量是不是大杯的 。
1
3
检验: 80×6+240
80÷240
=720(毫升)
1
3
=
回顾解决问题的过程,你有什么体会?
想一想,在以前的学习中,我们曾经运用假设的策略解决过哪些问题?
我们用过的假设策略
运用策略
计算除数是两位数的除法,把除数看作整十数试商
我们用过的假设策略
运用策略
把接近整百或整十的数看作整百或整十数,估算出大数的结果。
我们用过的假设策略
和是72
差是12
甲数
乙数
甲数和乙数各是多少?
运用策略
已知两个数的和与差,假设两个数同样多,分别求出这两个数。
3辆大货车和4辆小货车共运货30吨,大货车的载重量是小货车的2倍。两种货车的载重量各是多少吨?
(1)
1辆大货车运的货,需要(
)辆小货车才能运完。
2
10
30
÷10=3(吨)
3
×2=6(吨)
答:大货车的载重量是6吨,小货车的载重量是3吨。
第一关
3
×2=6(辆)
6
+
4=10(辆)
(2)
假设全部用小货车来运,需要(
)辆。
小:
大:
3辆大货车和4辆小货车共运货30吨,大货车的载重量是小货车的2倍。两种货车的载重量各是多少吨?
假设全部用大货车运,4辆小货车可以换成(
)辆大货车,一共需要(
)辆。
2
5
30
÷5=6(吨)
答:大货车的载重量是6吨,小货车的载重量是3吨。
6
÷2
=
3(吨)
4
÷2
=
2(辆)
2
+
3
=
5(辆)
第一关
大:
小:
一张桌子和4把椅子的总价是2700元,椅子的单价
是桌子的
。桌子和椅子的单价各是多少?
假设全部买椅子,
1张桌子可以换成(
)把椅子,一共(
)把椅子。
5
9
2700
÷9=300(元)
300
×5=1500(元)
答:桌子的单价是1500元,
椅子的单价是300元。
第二关
5
+
4=9(把)
椅子:
桌子:
三言两语
(3)通过这节课的学习,你有哪些收获?
还有哪些遗憾?
(1)这节课,你对哪个环节记忆最深刻?
(2)学了这节课,你想对老师说点什么?
有什么意见?
假设全部用小纸箱装
小纸箱:
大纸箱:
200÷(6+2×2)
=200÷10
=20(双)
20×2=40(双)
假设全部用大纸箱装
大纸箱:
小纸箱:
200÷(6÷2+2)
=200÷5
=40(双)
40÷2=20(双)
再
见
谢
谢
2、解决问题的策略(2)
6
1个菠萝与(
)个桃一样重。
(1)
(2)
笔记本的单价是练习本的5倍。买4本笔记本的钱可以买(
)本练习本。
20
热热身
1、小明把720毫升果汁倒入9个同样容量的小杯里,正好都倒满,
?
720÷9=80(毫升)
答:每个小杯的容量是80毫升。
每个小杯的容量是多少毫升
先根据条件提出问题,再列式解答。
2、小明把720毫升果汁倒入3个同样容量的大杯里,正好都倒满,
?
720÷3=240(毫升)
答:每个大杯的容量是240毫升。
每个大杯的容量是多少毫升
3、小明把720毫升果汁倒入6个小杯和1个大杯中,正好都倒满。
720毫升
小杯的容量是大杯的
,
小杯和大杯的容量各是多少毫升
?
?
6个小杯容量
+
1个大杯容量=
720毫升
1个大杯容量=
3个小杯容量
720毫升
假设把720毫升果汁全部倒入小杯
假设把720毫升果汁全部倒入大杯
6个小杯:
x毫升
3x毫升
1个大杯:
720毫升
选择一种方法列式解答,并进行检验。
假设把720毫升果汁
全部倒入小杯
小杯:1×3+6=9(杯)
大杯:
720÷9=80(毫升)
80×3=240(毫升)
720÷3=240(毫升)
240÷3
=
80
(毫升)
6÷3+1=3(杯)
假设把720毫升果汁
全部倒入大杯
大杯:
小杯:
列方程解答。
解:设小杯的容量是x毫升,则大杯容量是3x
毫升。
6个小杯的容量+1个大杯的容量=720毫升
大杯:80
×
3
=
240(毫升)
χ
=
720
÷
9
9χ
=
720
6χ
+
3χ
=
720
χ
=
80
检验:
★检验时要看我们所求答案是否符合题目中所有的条件。
1、看6个小杯和1个大杯的果汁是不是一共720毫升;
2、小杯的容量是不是大杯的 。
1
3
检验: 80×6+240
80÷240
=720(毫升)
1
3
=
回顾解决问题的过程,你有什么体会?
想一想,在以前的学习中,我们曾经运用假设的策略解决过哪些问题?
我们用过的假设策略
运用策略
计算除数是两位数的除法,把除数看作整十数试商
我们用过的假设策略
运用策略
把接近整百或整十的数看作整百或整十数,估算出大数的结果。
我们用过的假设策略
和是72
差是12
甲数
乙数
甲数和乙数各是多少?
运用策略
已知两个数的和与差,假设两个数同样多,分别求出这两个数。
3辆大货车和4辆小货车共运货30吨,大货车的载重量是小货车的2倍。两种货车的载重量各是多少吨?
(1)
1辆大货车运的货,需要(
)辆小货车才能运完。
2
10
30
÷10=3(吨)
3
×2=6(吨)
答:大货车的载重量是6吨,小货车的载重量是3吨。
第一关
3
×2=6(辆)
6
+
4=10(辆)
(2)
假设全部用小货车来运,需要(
)辆。
小:
大:
3辆大货车和4辆小货车共运货30吨,大货车的载重量是小货车的2倍。两种货车的载重量各是多少吨?
假设全部用大货车运,4辆小货车可以换成(
)辆大货车,一共需要(
)辆。
2
5
30
÷5=6(吨)
答:大货车的载重量是6吨,小货车的载重量是3吨。
6
÷2
=
3(吨)
4
÷2
=
2(辆)
2
+
3
=
5(辆)
第一关
大:
小:
一张桌子和4把椅子的总价是2700元,椅子的单价
是桌子的
。桌子和椅子的单价各是多少?
假设全部买椅子,
1张桌子可以换成(
)把椅子,一共(
)把椅子。
5
9
2700
÷9=300(元)
300
×5=1500(元)
答:桌子的单价是1500元,
椅子的单价是300元。
第二关
5
+
4=9(把)
椅子:
桌子:
三言两语
(3)通过这节课的学习,你有哪些收获?
还有哪些遗憾?
(1)这节课,你对哪个环节记忆最深刻?
(2)学了这节课,你想对老师说点什么?
有什么意见?
假设全部用小纸箱装
小纸箱:
大纸箱:
200÷(6+2×2)
=200÷10
=20(双)
20×2=40(双)
假设全部用大纸箱装
大纸箱:
小纸箱:
200÷(6÷2+2)
=200÷5
=40(双)
40÷2=20(双)
再
见
谢
谢
