鲁教版(五四制)六上 1.2.1展开与折叠 课件(24张PPT)
文档属性
| 名称 | 鲁教版(五四制)六上 1.2.1展开与折叠 课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 361.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-02 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
第一章
丰富的图形世界
学习新知
检测反馈
2 展开与折叠(第1课时)
折纸活动
你会折叠纸船和千纸鹤吗?
你能想象包装纸盒的展开图是什么样吗?
在生活中,我们经常见到正方体形状的盒子.为了设计和制作的需要,我们应了解正方体盒子展开后的平面图形.
探究活动1 你能得到哪些形状的平面图形
思考
2.比较是否有重复的,有些展开图通过旋转后是一样的.
1.以小组为单位,用手中的剪刀将准备好的正方体的表面沿某些棱剪开,
说一说是怎样剪的.
学
习
新
知
3.把正方体中任意两个相对面作为上下底面,其余四面作为侧面,将上、下底面与侧面相连的四条棱各任意剪开三条,再将四条侧棱任意剪开一条,就可以得到正方体的平面展开图.
将一个正方体的表面沿某些棱剪开,展成一个平面图形,如何剪可得到如下图所示的平面图形?
小活动
探究活动2
如何剪可得到指定的平面图形
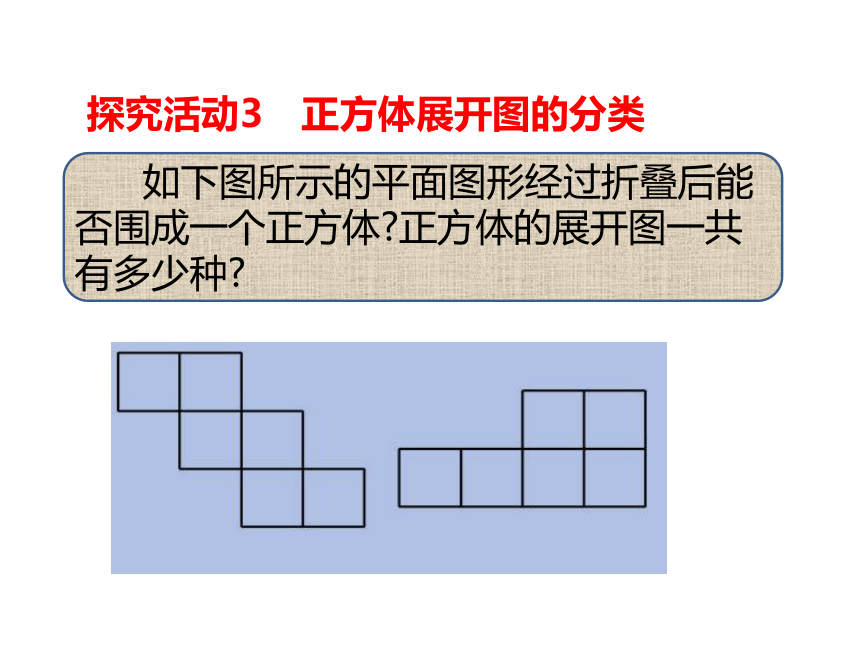
探究活动3 正方体展开图的分类
如下图所示的平面图形经过折叠后能否围成一个正方体?正方体的展开图一共有多少种?
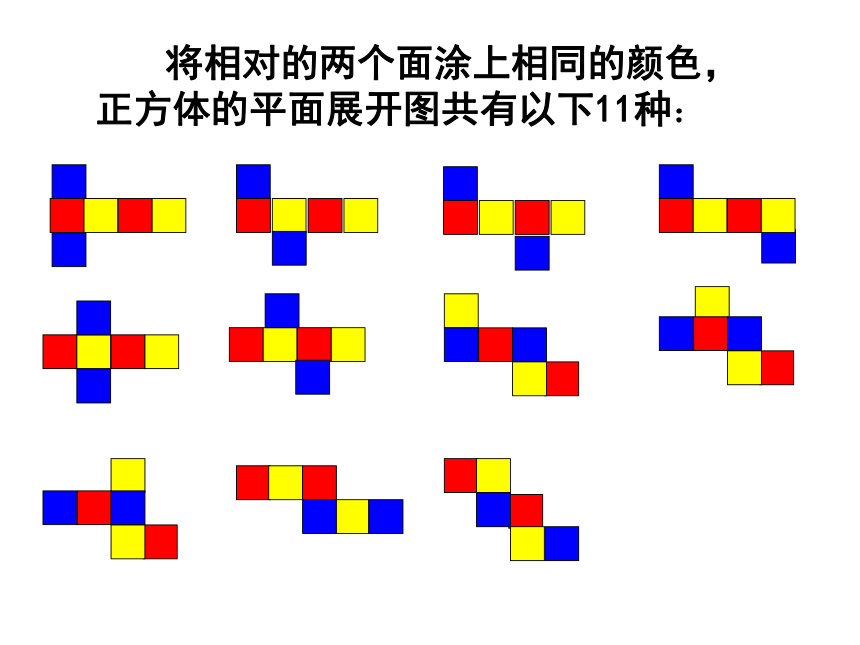
将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种:
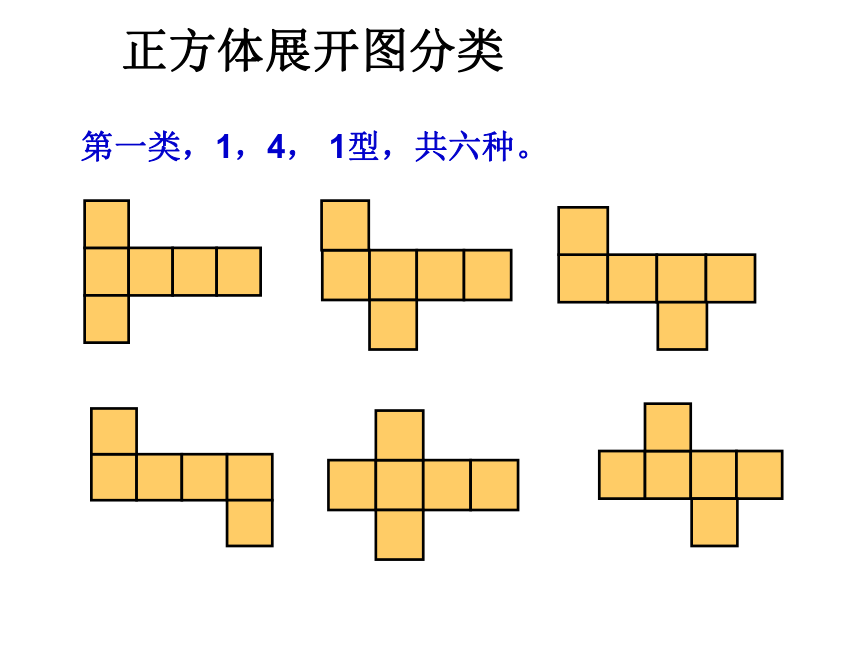
第一类,1,4,
1型,共六种。
正方体展开图分类
第二类,2,3,1型,共三种。
第三类,2,2,2型,只有一种。
第四类,3,3型,只有一种。
一四一,
二三一,
一在图层可任意,
三个二,
成阶梯,两个三,
目状连.
总结规律
特别说明:“一线”不过四,“田凹”应弃之,“2-4”不可取.
探究活动4
确定正方体展开图各个面的相对面
如图所示的平面图形可以折成一个正方体的盒子.折好以后,与
1
相邻的数是什么?相对的数是什么?先想一想,再具体折一折,看看你的想法是否正确.
与1相邻的数是2,4,5,6,相对的数是3.
知识拓展
正方体的展开图多种多样,注意不要遗漏也不要重复,同时注意展开图有“田”字形或“凹”字形时,不能围成正方体,即该展开图不是正方体的展开图.
一、判断给定的图形是不是正方体的展开图
正方体的平面展开图的几种题型
如图所示的图形中,哪些可以折叠成无盖的正方体?
可以
可以
可以
可以
可以
可以
可以
可以
二、找正方体相邻或相对的面
1.从展开图找.
如右图所示的是一个正方体的展开图,如果正方体相对的面上标注的值相同,那么x= ,y= .?
〔解析〕“2x”与“8”中间隔一个正方形,是相对的面,“y”与“10”是相对的面.所以x=4,y=10.
〔答案〕 4 10
4
10
如下图所示的是一个正方体的三种不同的放置方式,该正方体的表面分别标上数字1,2,3,4,5,6,则下底面标有的数字依次是 .?
〔解析〕 先找相邻的面,余下的面就是相对的面.上图出现最多的是面“3”,和面“3”相连的有面“2”“4”“5”“6”,余下的面“1”就和面“3”相对.再看面“6”,和面“6”相邻的有面“2”“3”“4”和面“3”相对的面“1”必和面“6”相邻,故面“6”和面“5”相对,余下的是面“4”和面“2”相对,下底面标有的数字依次是2,5,1.故填2,5,1.
2,5,1
B
A
C
D
小丽制作了一个如下图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是
( )
〔解析〕基本方法是先定上下,后定左右,可知A正确.故选A.
A
1.下列各图形中,经过折叠能围成一个正方体的是
( )
检测反馈
解析:由平面图形的折叠及正方体的展开图解题,注意只要有“田”“凹”字格的展开图都不是正方体的平面展开图.A.可以折叠成一个正方体;B.是“凹”字格,故不能折叠成一个正方体;C.折叠后有两个面重合,缺少一个底面,所以也不能折叠成一个正方体;D.是“田”字格,故不能折叠成一个正方体.故选A.
1.下列各图形中,经过折叠能围成一个正方体的是(
)
A
2.如右图所示的是一个正方体的平面展开图,则原正方体中“梦”字所在的面相对的面上标的字是
( )
A.大
B.伟
C.国 D.的
D
解析:正方体的平面展开图,相对
的面之间一定相隔一个正方形,根据这一特点,所以面“伟”与面“国”相对,面“大”与面“中”相对,面“的”与
面“梦”相对.故选D.
3.如下图所示的是一个正方体,它的平面展开图可能是下面四个展开图中的
( )
解析:由正方体可得:4,6,8所在的平面不可能是对面的关系.对于A,满足条件;对于B,4,8所在的平面相对,不满足条件;
对于C,6,8所在的平面相对,不满足条件;对于D,6,8所在的平面相对,不满足条件.故选A.
A
4.如右图所示,要使图中的展开图折叠成正方体后,相对面上的两个数字之和为7,则x= ,y= .?
解析:
由图可知面“x”与面“1”相对,面“y”与面“3”相对,故可得x=6,y=4.
答案:
6 4
6
4
2
1
3
x
y
【必做题】
教材第10页习题1.3的1,2题.
【选做题】
教材第11页习题1.3的3,4题.
布置作业
第一章
丰富的图形世界
学习新知
检测反馈
2 展开与折叠(第1课时)
折纸活动
你会折叠纸船和千纸鹤吗?
你能想象包装纸盒的展开图是什么样吗?
在生活中,我们经常见到正方体形状的盒子.为了设计和制作的需要,我们应了解正方体盒子展开后的平面图形.
探究活动1 你能得到哪些形状的平面图形
思考
2.比较是否有重复的,有些展开图通过旋转后是一样的.
1.以小组为单位,用手中的剪刀将准备好的正方体的表面沿某些棱剪开,
说一说是怎样剪的.
学
习
新
知
3.把正方体中任意两个相对面作为上下底面,其余四面作为侧面,将上、下底面与侧面相连的四条棱各任意剪开三条,再将四条侧棱任意剪开一条,就可以得到正方体的平面展开图.
将一个正方体的表面沿某些棱剪开,展成一个平面图形,如何剪可得到如下图所示的平面图形?
小活动
探究活动2
如何剪可得到指定的平面图形
探究活动3 正方体展开图的分类
如下图所示的平面图形经过折叠后能否围成一个正方体?正方体的展开图一共有多少种?
将相对的两个面涂上相同的颜色,正方体的平面展开图共有以下11种:
第一类,1,4,
1型,共六种。
正方体展开图分类
第二类,2,3,1型,共三种。
第三类,2,2,2型,只有一种。
第四类,3,3型,只有一种。
一四一,
二三一,
一在图层可任意,
三个二,
成阶梯,两个三,
目状连.
总结规律
特别说明:“一线”不过四,“田凹”应弃之,“2-4”不可取.
探究活动4
确定正方体展开图各个面的相对面
如图所示的平面图形可以折成一个正方体的盒子.折好以后,与
1
相邻的数是什么?相对的数是什么?先想一想,再具体折一折,看看你的想法是否正确.
与1相邻的数是2,4,5,6,相对的数是3.
知识拓展
正方体的展开图多种多样,注意不要遗漏也不要重复,同时注意展开图有“田”字形或“凹”字形时,不能围成正方体,即该展开图不是正方体的展开图.
一、判断给定的图形是不是正方体的展开图
正方体的平面展开图的几种题型
如图所示的图形中,哪些可以折叠成无盖的正方体?
可以
可以
可以
可以
可以
可以
可以
可以
二、找正方体相邻或相对的面
1.从展开图找.
如右图所示的是一个正方体的展开图,如果正方体相对的面上标注的值相同,那么x= ,y= .?
〔解析〕“2x”与“8”中间隔一个正方形,是相对的面,“y”与“10”是相对的面.所以x=4,y=10.
〔答案〕 4 10
4
10
如下图所示的是一个正方体的三种不同的放置方式,该正方体的表面分别标上数字1,2,3,4,5,6,则下底面标有的数字依次是 .?
〔解析〕 先找相邻的面,余下的面就是相对的面.上图出现最多的是面“3”,和面“3”相连的有面“2”“4”“5”“6”,余下的面“1”就和面“3”相对.再看面“6”,和面“6”相邻的有面“2”“3”“4”和面“3”相对的面“1”必和面“6”相邻,故面“6”和面“5”相对,余下的是面“4”和面“2”相对,下底面标有的数字依次是2,5,1.故填2,5,1.
2,5,1
B
A
C
D
小丽制作了一个如下图所示的正方体礼品盒,其对面图案都相同,那么这个正方体的平面展开图可能是
( )
〔解析〕基本方法是先定上下,后定左右,可知A正确.故选A.
A
1.下列各图形中,经过折叠能围成一个正方体的是
( )
检测反馈
解析:由平面图形的折叠及正方体的展开图解题,注意只要有“田”“凹”字格的展开图都不是正方体的平面展开图.A.可以折叠成一个正方体;B.是“凹”字格,故不能折叠成一个正方体;C.折叠后有两个面重合,缺少一个底面,所以也不能折叠成一个正方体;D.是“田”字格,故不能折叠成一个正方体.故选A.
1.下列各图形中,经过折叠能围成一个正方体的是(
)
A
2.如右图所示的是一个正方体的平面展开图,则原正方体中“梦”字所在的面相对的面上标的字是
( )
A.大
B.伟
C.国 D.的
D
解析:正方体的平面展开图,相对
的面之间一定相隔一个正方形,根据这一特点,所以面“伟”与面“国”相对,面“大”与面“中”相对,面“的”与
面“梦”相对.故选D.
3.如下图所示的是一个正方体,它的平面展开图可能是下面四个展开图中的
( )
解析:由正方体可得:4,6,8所在的平面不可能是对面的关系.对于A,满足条件;对于B,4,8所在的平面相对,不满足条件;
对于C,6,8所在的平面相对,不满足条件;对于D,6,8所在的平面相对,不满足条件.故选A.
A
4.如右图所示,要使图中的展开图折叠成正方体后,相对面上的两个数字之和为7,则x= ,y= .?
解析:
由图可知面“x”与面“1”相对,面“y”与面“3”相对,故可得x=6,y=4.
答案:
6 4
6
4
2
1
3
x
y
【必做题】
教材第10页习题1.3的1,2题.
【选做题】
教材第11页习题1.3的3,4题.
布置作业
