2021-2022学年人教版九年级数学上册22.1二次函数的图象和性质 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册22.1二次函数的图象和性质 同步练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 111.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 09:00:09 | ||
图片预览



文档简介
22.1
二次函数的图象和性质
同步练习题
2021-2022学年人教版九年级数学上册
A组(基础题)
1.二次函数图象上部分点的坐标对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-17
-17
-15
-11
-5
…
则该函数图象的对称轴直线是(
)
A.x=-3
B.x=-2.5
C.x=-2
D.x=0
2.如图,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是(
)
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
3.对二次函数y=x2+2x+3的性质描述正确的是(
)
A.函数图象开口向下
B.当x<0时,y随x的增大而向小
C.该函数图象的对称轴在y轴左侧
D.该函数图象与y轴的交点位于y轴负半轴
4.在抛物线y=x2-4x+m的图象上有三个点(-3,y1),(1,y2),(4,y3),则y1,y2,y3的大小关系为(
)
A.y2<y3<y1
B.y1<y2=y3
C.y1<y2<y3
D.y3<y2<y1
5.如图,抛物线y=-x2+4x+k与x轴交于点A和B,线段AB的长为2,则k的值是(
)
A.3
B.-3
C.-4
D.-5
6.在平面直角坐标系中,将抛物线y=x2-(m-1)x+m(m>1)沿y轴向下平移3个单位长度,则平移后得到的抛物线的顶点一定在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知抛物线y=x2+bx+c的部分图象如图所示,若-1)
A.-3≤y<0
B.-4≤y≤-3
C.-4D.-4≤y<0
8.若抛物线y=x2+ax+b与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=2,将此抛物线向左平移2个单位长度,再向上平移3个单位长度得到的抛物线过点(
)
A.(1,0)
B.(1,8)
C.(1,6)
D.(-1,4)
B组(中档题)
9.若二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为______.
10.在平面直角坐标系中,抛物线y=2(x-1)2+1的图象关于y轴对称的抛物线的解析式是______.
11.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是______.
12.已知二次函数y=ax2的图象经过点P(2,2),将该图象向右平移,当它再次经过点P时,所得抛物线的函数解析式为______.
13.已知二次函数y=mx2-2x+1,当x<时,y的值随x值的增大而减小,则m的取值范围是______.
14.对于二次函数y=x2-2mx-3,下列说法正确的是______.
①它的图象与y轴的交点坐标为(0,-3).
②若当x≤1时y随x的增大而减小,则m=1.
③若将它的图象向左平移3个单位长度后经过原点,则m=-1.
④若当x=-8时的函数值与x=2
020时的函数值相等,则当x=2
012时的函数值为-3.
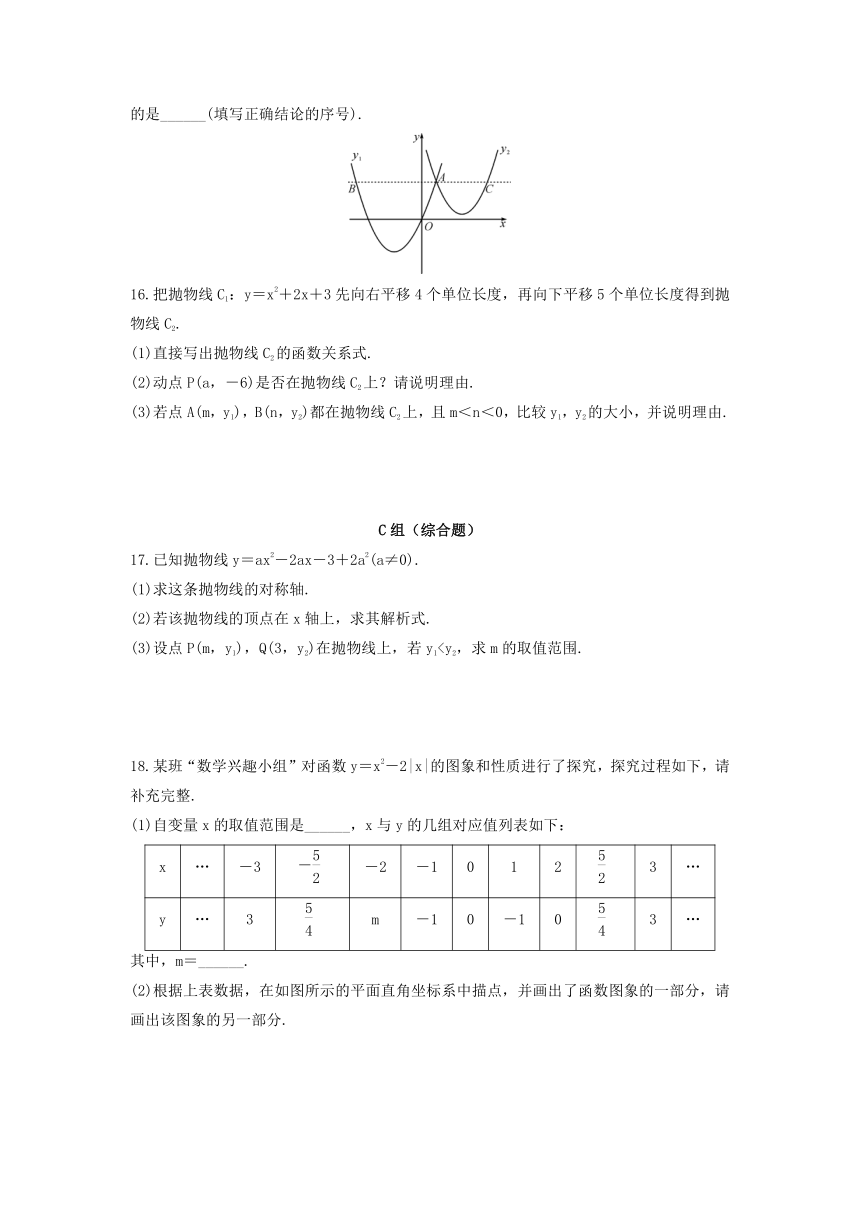
15.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②当x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的垂直平分线.正确的是______(填写正确结论的序号).
16.把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式.
(2)动点P(a,-6)是否在抛物线C2上?请说明理由.
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
C组(综合题)
17.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴.
(2)若该抛物线的顶点在x轴上,求其解析式.
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y118.某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是______,x与y的几组对应值列表如下:
x
…
-3
-
-2
-1
0
1
2
3
…
y
…
3
m
-1
0
-1
0
3
…
其中,m=______.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
参考答案
22.1
二次函数的图象和性质
同步练习题
2021-2022学年人教版九年级数学上册
A组(基础题)
1.二次函数图象上部分点的坐标对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-17
-17
-15
-11
-5
…
则该函数图象的对称轴直线是(B)
A.x=-3
B.x=-2.5
C.x=-2
D.x=0
2.如图,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是(D)
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
3.对二次函数y=x2+2x+3的性质描述正确的是(C)
A.函数图象开口向下
B.当x<0时,y随x的增大而向小
C.该函数图象的对称轴在y轴左侧
D.该函数图象与y轴的交点位于y轴负半轴
4.在抛物线y=x2-4x+m的图象上有三个点(-3,y1),(1,y2),(4,y3),则y1,y2,y3的大小关系为(A)
A.y2<y3<y1
B.y1<y2=y3
C.y1<y2<y3
D.y3<y2<y1
5.如图,抛物线y=-x2+4x+k与x轴交于点A和B,线段AB的长为2,则k的值是(B)
A.3
B.-3
C.-4
D.-5
6.在平面直角坐标系中,将抛物线y=x2-(m-1)x+m(m>1)沿y轴向下平移3个单位长度,则平移后得到的抛物线的顶点一定在(D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知抛物线y=x2+bx+c的部分图象如图所示,若-1A.-3≤y<0
B.-4≤y≤-3
C.-4D.-4≤y<0
8.若抛物线y=x2+ax+b与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=2,将此抛物线向左平移2个单位长度,再向上平移3个单位长度得到的抛物线过点(A)
A.(1,0)
B.(1,8)
C.(1,6)
D.(-1,4)
B组(中档题)
9.若二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为2.
10.在平面直角坐标系中,抛物线y=2(x-1)2+1的图象关于y轴对称的抛物线的解析式是y=2(x+1)2+1.
11.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是(1,4).
12.已知二次函数y=ax2的图象经过点P(2,2),将该图象向右平移,当它再次经过点P时,所得抛物线的函数解析式为y=(x-4)2.
13.已知二次函数y=mx2-2x+1,当x<时,y的值随x值的增大而减小,则m的取值范围是0<m≤3.
14.对于二次函数y=x2-2mx-3,下列说法正确的是①④.
①它的图象与y轴的交点坐标为(0,-3).
②若当x≤1时y随x的增大而减小,则m=1.
③若将它的图象向左平移3个单位长度后经过原点,则m=-1.
④若当x=-8时的函数值与x=2
020时的函数值相等,则当x=2
012时的函数值为-3.
15.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②当x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的垂直平分线.正确的是①③④(填写正确结论的序号).
16.把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式.
(2)动点P(a,-6)是否在抛物线C2上?请说明理由.
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
解:(1)∵y=x2+2x+3=(x+1)2+2,
∴把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=(x+1-4)2+2-5,即y=(x-3)2-3.
∴抛物线C2的函数关系式为y=(x-3)2-3.
(2)动点P(a,-6)不在抛物线C2上,理由如下:
∵抛物线C2的函数关系式为y=(x-3)2-3,
∴函数的最小值为-3.
∵-6<-3,∴动点P(a,-6)不在抛物线C2上.
(3)∵抛物线C2的函数关系式为y=(x-3)2-3,
∴抛物线的开口向上,对称轴为x=3.
∴当x<3时,y随x的增大而减小.
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0<3,∴y1>y2.
C组(综合题)
17.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴.
(2)若该抛物线的顶点在x轴上,求其解析式.
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1解:(1)这条抛物线的对称轴是直线x=-=1.
(2)∵y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,抛物线的顶点在x轴上,
∴2a2-a-3=0,解得a=或a=-1.
∴抛物线的解析式为
y=x2-3x+或y=-x2+2x-1.
(3)①当a>0时,∵点P(m,y1),Q(3,y2)在抛物线上,且y1∴-1②当a<0时,∵点P(m,y1),Q(3,y2)在抛物线上,且y1∴m>3或m<-1.
18.某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
-3
-
-2
-1
0
1
2
3
…
y
…
3
m
-1
0
-1
0
3
…
其中,m=0.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数图象的性质.
解:(2)如图所示.
(3)函数图象关于y轴对称;函数图象开口向上等,答案不唯一.
二次函数的图象和性质
同步练习题
2021-2022学年人教版九年级数学上册
A组(基础题)
1.二次函数图象上部分点的坐标对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-17
-17
-15
-11
-5
…
则该函数图象的对称轴直线是(
)
A.x=-3
B.x=-2.5
C.x=-2
D.x=0
2.如图,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是(
)
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
3.对二次函数y=x2+2x+3的性质描述正确的是(
)
A.函数图象开口向下
B.当x<0时,y随x的增大而向小
C.该函数图象的对称轴在y轴左侧
D.该函数图象与y轴的交点位于y轴负半轴
4.在抛物线y=x2-4x+m的图象上有三个点(-3,y1),(1,y2),(4,y3),则y1,y2,y3的大小关系为(
)
A.y2<y3<y1
B.y1<y2=y3
C.y1<y2<y3
D.y3<y2<y1
5.如图,抛物线y=-x2+4x+k与x轴交于点A和B,线段AB的长为2,则k的值是(
)
A.3
B.-3
C.-4
D.-5
6.在平面直角坐标系中,将抛物线y=x2-(m-1)x+m(m>1)沿y轴向下平移3个单位长度,则平移后得到的抛物线的顶点一定在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知抛物线y=x2+bx+c的部分图象如图所示,若-1
A.-3≤y<0
B.-4≤y≤-3
C.-4
8.若抛物线y=x2+ax+b与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=2,将此抛物线向左平移2个单位长度,再向上平移3个单位长度得到的抛物线过点(
)
A.(1,0)
B.(1,8)
C.(1,6)
D.(-1,4)
B组(中档题)
9.若二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为______.
10.在平面直角坐标系中,抛物线y=2(x-1)2+1的图象关于y轴对称的抛物线的解析式是______.
11.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是______.
12.已知二次函数y=ax2的图象经过点P(2,2),将该图象向右平移,当它再次经过点P时,所得抛物线的函数解析式为______.
13.已知二次函数y=mx2-2x+1,当x<时,y的值随x值的增大而减小,则m的取值范围是______.
14.对于二次函数y=x2-2mx-3,下列说法正确的是______.
①它的图象与y轴的交点坐标为(0,-3).
②若当x≤1时y随x的增大而减小,则m=1.
③若将它的图象向左平移3个单位长度后经过原点,则m=-1.
④若当x=-8时的函数值与x=2
020时的函数值相等,则当x=2
012时的函数值为-3.
15.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②当x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的垂直平分线.正确的是______(填写正确结论的序号).
16.把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式.
(2)动点P(a,-6)是否在抛物线C2上?请说明理由.
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
C组(综合题)
17.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴.
(2)若该抛物线的顶点在x轴上,求其解析式.
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1
(1)自变量x的取值范围是______,x与y的几组对应值列表如下:
x
…
-3
-
-2
-1
0
1
2
3
…
y
…
3
m
-1
0
-1
0
3
…
其中,m=______.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
参考答案
22.1
二次函数的图象和性质
同步练习题
2021-2022学年人教版九年级数学上册
A组(基础题)
1.二次函数图象上部分点的坐标对应值列表如下:
x
…
-3
-2
-1
0
1
…
y
…
-17
-17
-15
-11
-5
…
则该函数图象的对称轴直线是(B)
A.x=-3
B.x=-2.5
C.x=-2
D.x=0
2.如图,二次函数y=a(x+1)2+k的图象与x轴交于A(-3,0),B两点,下列说法错误的是(D)
A.a<0
B.图象的对称轴为直线x=-1
C.点B的坐标为(1,0)
D.当x<0时,y随x的增大而增大
3.对二次函数y=x2+2x+3的性质描述正确的是(C)
A.函数图象开口向下
B.当x<0时,y随x的增大而向小
C.该函数图象的对称轴在y轴左侧
D.该函数图象与y轴的交点位于y轴负半轴
4.在抛物线y=x2-4x+m的图象上有三个点(-3,y1),(1,y2),(4,y3),则y1,y2,y3的大小关系为(A)
A.y2<y3<y1
B.y1<y2=y3
C.y1<y2<y3
D.y3<y2<y1
5.如图,抛物线y=-x2+4x+k与x轴交于点A和B,线段AB的长为2,则k的值是(B)
A.3
B.-3
C.-4
D.-5
6.在平面直角坐标系中,将抛物线y=x2-(m-1)x+m(m>1)沿y轴向下平移3个单位长度,则平移后得到的抛物线的顶点一定在(D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.已知抛物线y=x2+bx+c的部分图象如图所示,若-1
B.-4≤y≤-3
C.-4
8.若抛物线y=x2+ax+b与x轴两个交点间的距离为4,称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=2,将此抛物线向左平移2个单位长度,再向上平移3个单位长度得到的抛物线过点(A)
A.(1,0)
B.(1,8)
C.(1,6)
D.(-1,4)
B组(中档题)
9.若二次函数y=mx2+x+m(m-2)的图象经过原点,则m的值为2.
10.在平面直角坐标系中,抛物线y=2(x-1)2+1的图象关于y轴对称的抛物线的解析式是y=2(x+1)2+1.
11.已知A(0,3),B(2,3)是抛物线y=-x2+bx+c上两点,该抛物线的顶点坐标是(1,4).
12.已知二次函数y=ax2的图象经过点P(2,2),将该图象向右平移,当它再次经过点P时,所得抛物线的函数解析式为y=(x-4)2.
13.已知二次函数y=mx2-2x+1,当x<时,y的值随x值的增大而减小,则m的取值范围是0<m≤3.
14.对于二次函数y=x2-2mx-3,下列说法正确的是①④.
①它的图象与y轴的交点坐标为(0,-3).
②若当x≤1时y随x的增大而减小,则m=1.
③若将它的图象向左平移3个单位长度后经过原点,则m=-1.
④若当x=-8时的函数值与x=2
020时的函数值相等,则当x=2
012时的函数值为-3.
15.如图,抛物线y1=a(x+2)2+m过原点,与抛物线y2=(x-3)2+n交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.下列结论:①两条抛物线的对称轴距离为5;②当x=0时,y2=5;③当x>3时,y1-y2>0;④y轴是线段BC的垂直平分线.正确的是①③④(填写正确结论的序号).
16.把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2.
(1)直接写出抛物线C2的函数关系式.
(2)动点P(a,-6)是否在抛物线C2上?请说明理由.
(3)若点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0,比较y1,y2的大小,并说明理由.
解:(1)∵y=x2+2x+3=(x+1)2+2,
∴把抛物线C1:y=x2+2x+3先向右平移4个单位长度,再向下平移5个单位长度得到抛物线C2:y=(x+1-4)2+2-5,即y=(x-3)2-3.
∴抛物线C2的函数关系式为y=(x-3)2-3.
(2)动点P(a,-6)不在抛物线C2上,理由如下:
∵抛物线C2的函数关系式为y=(x-3)2-3,
∴函数的最小值为-3.
∵-6<-3,∴动点P(a,-6)不在抛物线C2上.
(3)∵抛物线C2的函数关系式为y=(x-3)2-3,
∴抛物线的开口向上,对称轴为x=3.
∴当x<3时,y随x的增大而减小.
∵点A(m,y1),B(n,y2)都在抛物线C2上,且m<n<0<3,∴y1>y2.
C组(综合题)
17.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴.
(2)若该抛物线的顶点在x轴上,求其解析式.
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1
(2)∵y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,抛物线的顶点在x轴上,
∴2a2-a-3=0,解得a=或a=-1.
∴抛物线的解析式为
y=x2-3x+或y=-x2+2x-1.
(3)①当a>0时,∵点P(m,y1),Q(3,y2)在抛物线上,且y1
18.某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x
…
-3
-
-2
-1
0
1
2
3
…
y
…
3
m
-1
0
-1
0
3
…
其中,m=0.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数图象的性质.
解:(2)如图所示.
(3)函数图象关于y轴对称;函数图象开口向上等,答案不唯一.
同课章节目录
