2021-2022学年人教版九年级数学上册23.2.2关于原点对称的点的坐标同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册23.2.2关于原点对称的点的坐标同步练习题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 203.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:05:58 | ||
图片预览


文档简介
23.2.2关于原点对称的点的坐标同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是(
)
A.(2,3)
B.(-3,2)
C.(-3,-2)
D.(-2,-3)
2.在平面直角坐标系中,点(a,b)关于原点对称的点的坐标是(
)
A.(-a,-b)
B.(-b,-a)
C.(-a,b)
D.(b,a)
3.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是_______.
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为_______.
6.若点P(x,-3)与点Q(4,y)关于原点对称,则xy的值是(
)
A.12
B.-12
C.64
D.-64
7.若点P(m-1,5)与点Q(3,2-n)关于原点对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
8.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是(
)
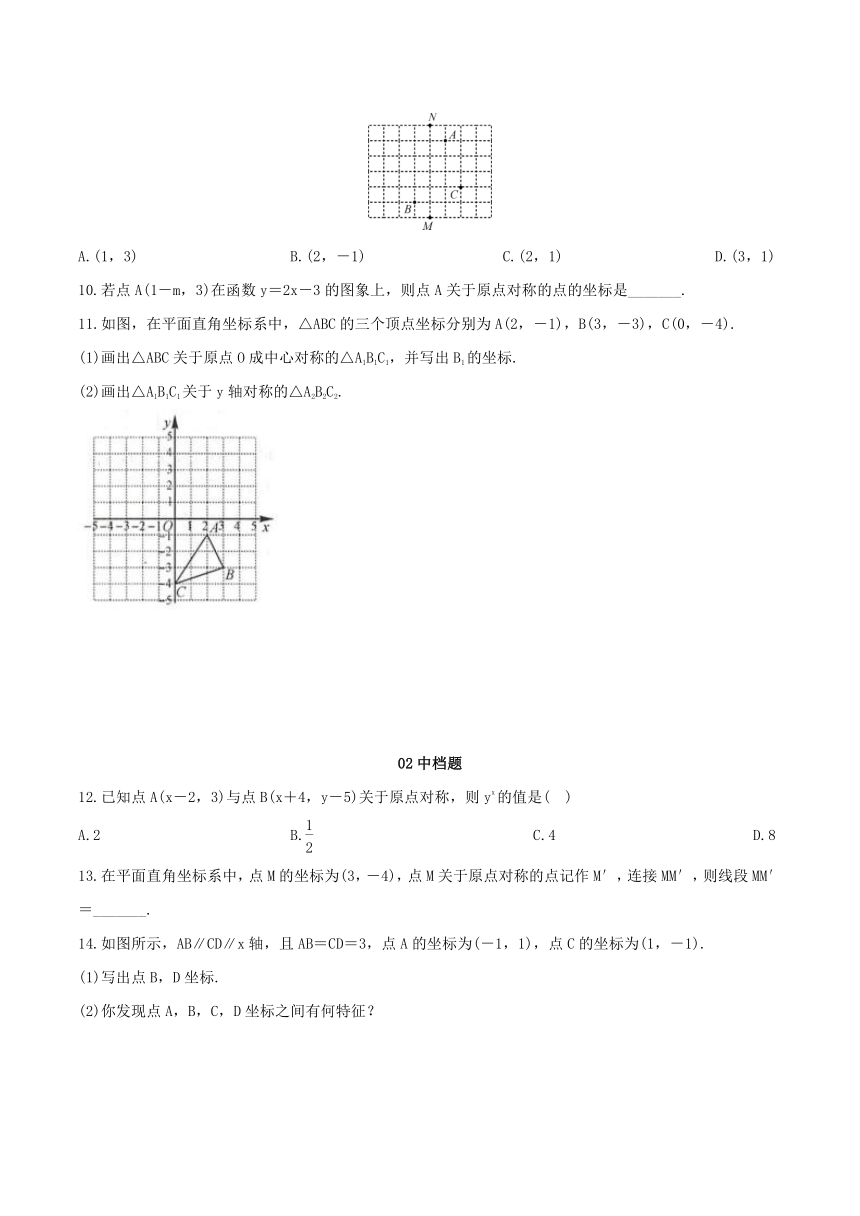
9.在如图所示的方格纸中,每个小正方形的边长均为1,若以MN所在的直线为y轴(向上为正方向),以小正方形的边长为1个单位长度建立平面直角坐标系,使点A与点B关于原点对称,则点C的坐标是(
)
A.(1,3)
B.(2,-1)
C.(2,1)
D.(3,1)
10.若点A(1-m,3)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是_______.
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
02中档题
12.已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则yx的值是(
)
A.2
B.
C.4
D.8
13.在平面直角坐标系中,点M的坐标为(3,-4),点M关于原点对称的点记作M′,连接MM′,则线段MM′=_______.
14.如图所示,AB∥CD∥x轴,且AB=CD=3,点A的坐标为(-1,1),点C的坐标为(1,-1).
(1)写出点B,D坐标.
(2)你发现点A,B,C,D坐标之间有何特征?
03综合题
15.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的△A1B1C1.
(2)请画出△ABC关于点(1,0)成中心对称的△A2B2C2.
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标.
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
参考答案
23.2.2关于原点对称的点的坐标同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是(C)
A.(2,3)
B.(-3,2)
C.(-3,-2)
D.(-2,-3)
2.在平面直角坐标系中,点(a,b)关于原点对称的点的坐标是(A)
A.(-a,-b)
B.(-b,-a)
C.(-a,b)
D.(b,a)
3.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是(1,-2).
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为A1(-2,-4),B1(-1,-1),C1(-3,1).
6.若点P(x,-3)与点Q(4,y)关于原点对称,则xy的值是(B)
A.12
B.-12
C.64
D.-64
7.若点P(m-1,5)与点Q(3,2-n)关于原点对称,则m+n的值是(C)
A.1
B.3
C.5
D.7
8.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是(C)
9.在如图所示的方格纸中,每个小正方形的边长均为1,若以MN所在的直线为y轴(向上为正方向),以小正方形的边长为1个单位长度建立平面直角坐标系,使点A与点B关于原点对称,则点C的坐标是(B)
A.(1,3)
B.(2,-1)
C.(2,1)
D.(3,1)
10.若点A(1-m,3)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是(-3,-3).
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
解:(1)△A1B1C1如图所示,B1(-3,3).
(2)△A2B2C2如图所示.
02中档题
12.已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则yx的值是(B)
A.2
B.
C.4
D.8
13.在平面直角坐标系中,点M的坐标为(3,-4),点M关于原点对称的点记作M′,连接MM′,则线段MM′=10.
14.如图所示,AB∥CD∥x轴,且AB=CD=3,点A的坐标为(-1,1),点C的坐标为(1,-1).
(1)写出点B,D坐标.
(2)你发现点A,B,C,D坐标之间有何特征?
解:(1)∵AB∥CD∥x轴,A(-1,1),C(1,-1),
∴点B,D的纵坐标分别是1,-1.
∵AB=CD=3,
∴B(2,1),D(-2,-1).
(2)∵A(-1,1),C(1,-1),即点A,C的横、纵坐标互为相反数,∴点A,C关于原点对称.
同理,点B,D关于原点对称.
03综合题
15.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的△A1B1C1.
(2)请画出△ABC关于点(1,0)成中心对称的△A2B2C2.
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标.
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,点M即为所求,点M的坐标为(-1,0).
(4)如图,点P即为所求,点P的坐标为(2,0).
2021-2022学年人教版九年级数学上册
01基础题
1.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是(
)
A.(2,3)
B.(-3,2)
C.(-3,-2)
D.(-2,-3)
2.在平面直角坐标系中,点(a,b)关于原点对称的点的坐标是(
)
A.(-a,-b)
B.(-b,-a)
C.(-a,b)
D.(b,a)
3.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是_______.
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为_______.
6.若点P(x,-3)与点Q(4,y)关于原点对称,则xy的值是(
)
A.12
B.-12
C.64
D.-64
7.若点P(m-1,5)与点Q(3,2-n)关于原点对称,则m+n的值是(
)
A.1
B.3
C.5
D.7
8.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是(
)
9.在如图所示的方格纸中,每个小正方形的边长均为1,若以MN所在的直线为y轴(向上为正方向),以小正方形的边长为1个单位长度建立平面直角坐标系,使点A与点B关于原点对称,则点C的坐标是(
)
A.(1,3)
B.(2,-1)
C.(2,1)
D.(3,1)
10.若点A(1-m,3)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是_______.
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
02中档题
12.已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则yx的值是(
)
A.2
B.
C.4
D.8
13.在平面直角坐标系中,点M的坐标为(3,-4),点M关于原点对称的点记作M′,连接MM′,则线段MM′=_______.
14.如图所示,AB∥CD∥x轴,且AB=CD=3,点A的坐标为(-1,1),点C的坐标为(1,-1).
(1)写出点B,D坐标.
(2)你发现点A,B,C,D坐标之间有何特征?
03综合题
15.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的△A1B1C1.
(2)请画出△ABC关于点(1,0)成中心对称的△A2B2C2.
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标.
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
参考答案
23.2.2关于原点对称的点的坐标同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.在平面直角坐标系中,点(3,2)关于原点对称的点的坐标是(C)
A.(2,3)
B.(-3,2)
C.(-3,-2)
D.(-2,-3)
2.在平面直角坐标系中,点(a,b)关于原点对称的点的坐标是(A)
A.(-a,-b)
B.(-b,-a)
C.(-a,b)
D.(b,a)
3.在平面直角坐标系中,点P(-3,m2+1)关于原点的对称点在(D)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,则点A′关于原点对称的点的坐标是(1,-2).
5.如图,在平面直角坐标系中,若△ABC与△A1B1C1关于原点对称,则点A1,B1,C1的坐标分别为A1(-2,-4),B1(-1,-1),C1(-3,1).
6.若点P(x,-3)与点Q(4,y)关于原点对称,则xy的值是(B)
A.12
B.-12
C.64
D.-64
7.若点P(m-1,5)与点Q(3,2-n)关于原点对称,则m+n的值是(C)
A.1
B.3
C.5
D.7
8.已知点P(a-3,2-a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是(C)
9.在如图所示的方格纸中,每个小正方形的边长均为1,若以MN所在的直线为y轴(向上为正方向),以小正方形的边长为1个单位长度建立平面直角坐标系,使点A与点B关于原点对称,则点C的坐标是(B)
A.(1,3)
B.(2,-1)
C.(2,1)
D.(3,1)
10.若点A(1-m,3)在函数y=2x-3的图象上,则点A关于原点对称的点的坐标是(-3,-3).
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,-1),B(3,-3),C(0,-4).
(1)画出△ABC关于原点O成中心对称的△A1B1C1,并写出B1的坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2.
解:(1)△A1B1C1如图所示,B1(-3,3).
(2)△A2B2C2如图所示.
02中档题
12.已知点A(x-2,3)与点B(x+4,y-5)关于原点对称,则yx的值是(B)
A.2
B.
C.4
D.8
13.在平面直角坐标系中,点M的坐标为(3,-4),点M关于原点对称的点记作M′,连接MM′,则线段MM′=10.
14.如图所示,AB∥CD∥x轴,且AB=CD=3,点A的坐标为(-1,1),点C的坐标为(1,-1).
(1)写出点B,D坐标.
(2)你发现点A,B,C,D坐标之间有何特征?
解:(1)∵AB∥CD∥x轴,A(-1,1),C(1,-1),
∴点B,D的纵坐标分别是1,-1.
∵AB=CD=3,
∴B(2,1),D(-2,-1).
(2)∵A(-1,1),C(1,-1),即点A,C的横、纵坐标互为相反数,∴点A,C关于原点对称.
同理,点B,D关于原点对称.
03综合题
15.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出将△ABC向左平移4个单位长度后得到的△A1B1C1.
(2)请画出△ABC关于点(1,0)成中心对称的△A2B2C2.
(3)若△A1B1C1绕点M旋转可以得到△A2B2C2,请直接写出点M的坐标.
(4)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C2即为所求.
(3)如图,点M即为所求,点M的坐标为(-1,0).
(4)如图,点P即为所求,点P的坐标为(2,0).
同课章节目录
