2021-2022学年人教版九年级数学上册23.1.3旋转作图同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册23.1.3旋转作图同步练习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 393.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:07:09 | ||
图片预览


文档简介
23.1.3旋转作图同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是(
)
2.如图,△ABC绕点0旋转后,顶点A的对应点为点D,试确定顶点B,C对应点的位置并画出旋转后的三角形.
3.如图,画出四边形ABCD绕点O逆时针旋转90°后的图形.
4.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为(
)
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
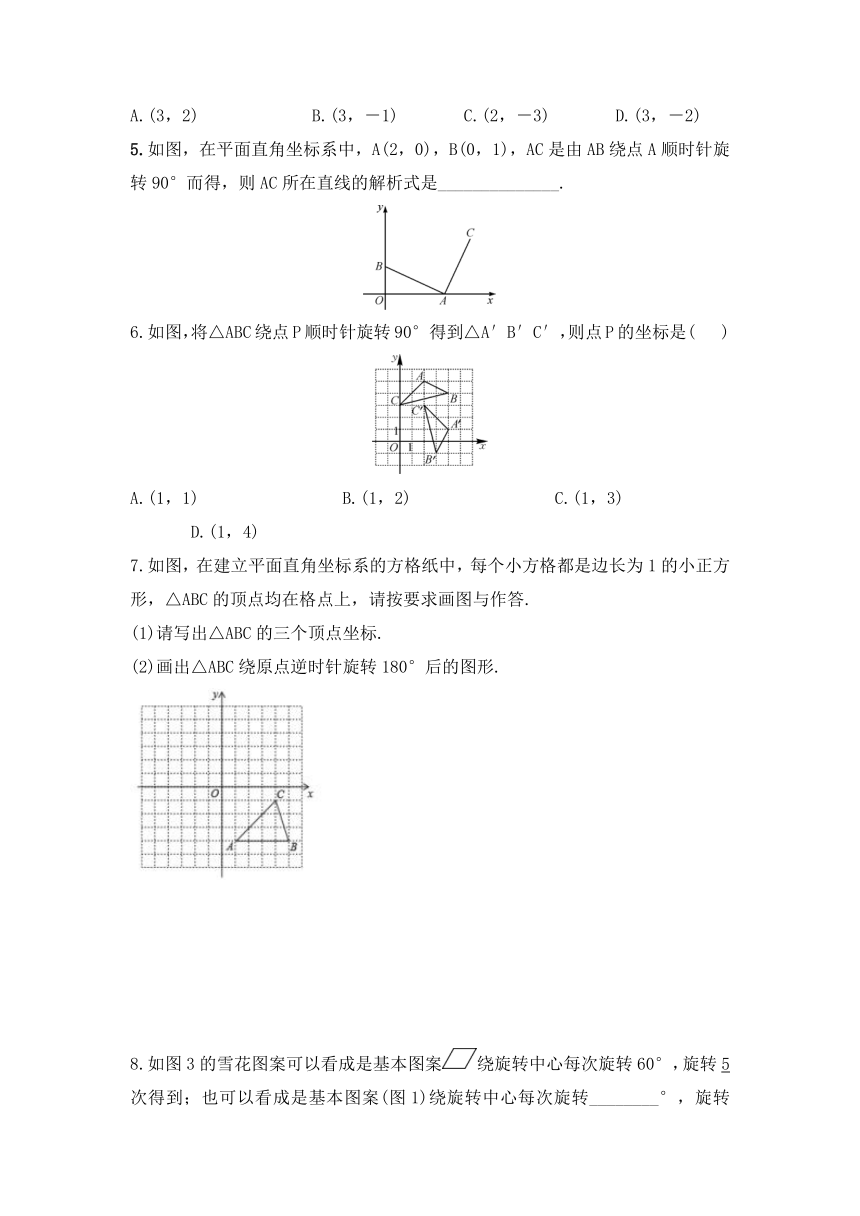
5.如图,在平面直角坐标系中,A(2,0),B(0,1),AC是由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是______________.
6.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
7.如图,在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.
(1)请写出△ABC的三个顶点坐标.
(2)画出△ABC绕原点逆时针旋转180°后的图形.
8.如图3的雪花图案可以看成是基本图案绕旋转中心每次旋转60°,旋转5次得到;也可以看成是基本图案(图1)绕旋转中心每次旋转________°,旋转_________次得到;还可以看成是基本图案(图2)绕旋转中心旋转_______°得到.
9.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是_____________.
02中档题
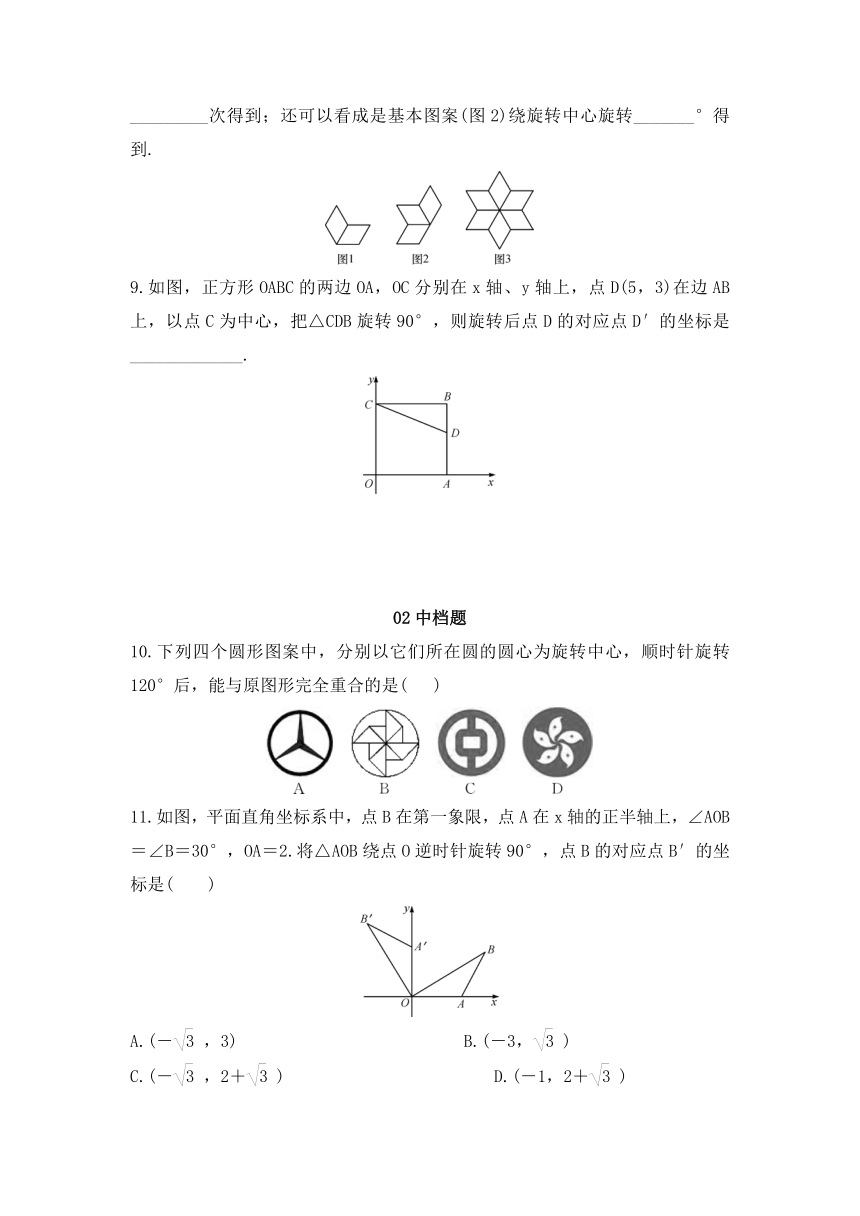
10.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(
)
11.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(
)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
12.如图,在5×5的网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°得到△OA′B′,A,B的对应点分别为A′,B′,则A,B′之间的距离为(
)
A.2
B.5
C.
D.
13.旋转是一种常见的全等变换,图1中的△ABC绕点O旋转后得到△A′B′C′,我们称点A和点A′、点B和点B′、点C和点C′分别是对应点,把点O称为旋转中心.
(1)观察图1,想一想,旋转变换具有哪些特点呢?请写出其中三个特点.
(2)图2中,△ABC顺时针旋转后,线段AB的对应线段为线段DE(点A和点D、点B和点E分别是对应点),请你利用圆规、直尺等工具,
①作出旋转中心O.
②作出△ABC绕点O旋转后的△DEF.
参考答案
23.1.3旋转作图同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是(C)
2.如图,△ABC绕点0旋转后,顶点A的对应点为点D,试确定顶点B,C对应点的位置并画出旋转后的三角形.
解:如图,顶点B对应点的位置在点E处,△DEC为△ABC绕点0旋转后得到的三角形.
3.如图,画出四边形ABCD绕点O逆时针旋转90°后的图形.
解:如图所示,四边形EFGH即为所求.
4.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为(D)
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
5.如图,在平面直角坐标系中,A(2,0),B(0,1),AC是由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是y=2x-4.
6.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(B)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
7.如图,在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.
(1)请写出△ABC的三个顶点坐标.
(2)画出△ABC绕原点逆时针旋转180°后的图形.
解:(1)A(1,-4),B(5,-4),C(4,-1).
(2)如图所示,△A1B1C1即为所求.
8.如图3的雪花图案可以看成是基本图案绕旋转中心每次旋转60°,旋转5次得到;也可以看成是基本图案(图1)绕旋转中心每次旋转120°,旋转2次得到;还可以看成是基本图案(图2)绕旋转中心旋转180°得到.
9.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(2,10)或(-2,0).
02中档题
10.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(A)
11.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(A)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
12.如图,在5×5的网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°得到△OA′B′,A,B的对应点分别为A′,B′,则A,B′之间的距离为(C)
A.2
B.5
C.
D.
13.旋转是一种常见的全等变换,图1中的△ABC绕点O旋转后得到△A′B′C′,我们称点A和点A′、点B和点B′、点C和点C′分别是对应点,把点O称为旋转中心.
(1)观察图1,想一想,旋转变换具有哪些特点呢?请写出其中三个特点.
(2)图2中,△ABC顺时针旋转后,线段AB的对应线段为线段DE(点A和点D、点B和点E分别是对应点),请你利用圆规、直尺等工具,
①作出旋转中心O.
②作出△ABC绕点O旋转后的△DEF.
解:(1)三个特点:
①对应点到旋转中心的距离相等;
②任意一对对应点与旋转中心的连线所成的角相等;
③两个三角形全等.
(2)连接AD,BE,分别作线段AD与BE的垂直平分线,交于点O,O就是旋转中心.
连接OC,作∠COM=∠BOE,
再在OM上截取OF=OC,
连接EF,DF,即可得到旋转后的△DEF.
2021-2022学年人教版九年级数学上册
01基础题
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是(
)
2.如图,△ABC绕点0旋转后,顶点A的对应点为点D,试确定顶点B,C对应点的位置并画出旋转后的三角形.
3.如图,画出四边形ABCD绕点O逆时针旋转90°后的图形.
4.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为(
)
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
5.如图,在平面直角坐标系中,A(2,0),B(0,1),AC是由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是______________.
6.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(
)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
7.如图,在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.
(1)请写出△ABC的三个顶点坐标.
(2)画出△ABC绕原点逆时针旋转180°后的图形.
8.如图3的雪花图案可以看成是基本图案绕旋转中心每次旋转60°,旋转5次得到;也可以看成是基本图案(图1)绕旋转中心每次旋转________°,旋转_________次得到;还可以看成是基本图案(图2)绕旋转中心旋转_______°得到.
9.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是_____________.
02中档题
10.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(
)
11.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(
)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
12.如图,在5×5的网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°得到△OA′B′,A,B的对应点分别为A′,B′,则A,B′之间的距离为(
)
A.2
B.5
C.
D.
13.旋转是一种常见的全等变换,图1中的△ABC绕点O旋转后得到△A′B′C′,我们称点A和点A′、点B和点B′、点C和点C′分别是对应点,把点O称为旋转中心.
(1)观察图1,想一想,旋转变换具有哪些特点呢?请写出其中三个特点.
(2)图2中,△ABC顺时针旋转后,线段AB的对应线段为线段DE(点A和点D、点B和点E分别是对应点),请你利用圆规、直尺等工具,
①作出旋转中心O.
②作出△ABC绕点O旋转后的△DEF.
参考答案
23.1.3旋转作图同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是(C)
2.如图,△ABC绕点0旋转后,顶点A的对应点为点D,试确定顶点B,C对应点的位置并画出旋转后的三角形.
解:如图,顶点B对应点的位置在点E处,△DEC为△ABC绕点0旋转后得到的三角形.
3.如图,画出四边形ABCD绕点O逆时针旋转90°后的图形.
解:如图所示,四边形EFGH即为所求.
4.如图,在平面直角坐标系中,将点P(2,3)绕原点O顺时针旋转90°得到点P′,则点P′的坐标为(D)
A.(3,2)
B.(3,-1)
C.(2,-3)
D.(3,-2)
5.如图,在平面直角坐标系中,A(2,0),B(0,1),AC是由AB绕点A顺时针旋转90°而得,则AC所在直线的解析式是y=2x-4.
6.如图,将△ABC绕点P顺时针旋转90°得到△A′B′C′,则点P的坐标是(B)
A.(1,1)
B.(1,2)
C.(1,3)
D.(1,4)
7.如图,在建立平面直角坐标系的方格纸中,每个小方格都是边长为1的小正方形,△ABC的顶点均在格点上,请按要求画图与作答.
(1)请写出△ABC的三个顶点坐标.
(2)画出△ABC绕原点逆时针旋转180°后的图形.
解:(1)A(1,-4),B(5,-4),C(4,-1).
(2)如图所示,△A1B1C1即为所求.
8.如图3的雪花图案可以看成是基本图案绕旋转中心每次旋转60°,旋转5次得到;也可以看成是基本图案(图1)绕旋转中心每次旋转120°,旋转2次得到;还可以看成是基本图案(图2)绕旋转中心旋转180°得到.
9.如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是(2,10)或(-2,0).
02中档题
10.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是(A)
11.如图,平面直角坐标系中,点B在第一象限,点A在x轴的正半轴上,∠AOB=∠B=30°,OA=2.将△AOB绕点O逆时针旋转90°,点B的对应点B′的坐标是(A)
A.(-,3)
B.(-3,)
C.(-,2+)
D.(-1,2+)
12.如图,在5×5的网格中,每个小正方形的边长均为1,点A,B,O都在格点上.若将△OAB绕点O逆时针旋转90°得到△OA′B′,A,B的对应点分别为A′,B′,则A,B′之间的距离为(C)
A.2
B.5
C.
D.
13.旋转是一种常见的全等变换,图1中的△ABC绕点O旋转后得到△A′B′C′,我们称点A和点A′、点B和点B′、点C和点C′分别是对应点,把点O称为旋转中心.
(1)观察图1,想一想,旋转变换具有哪些特点呢?请写出其中三个特点.
(2)图2中,△ABC顺时针旋转后,线段AB的对应线段为线段DE(点A和点D、点B和点E分别是对应点),请你利用圆规、直尺等工具,
①作出旋转中心O.
②作出△ABC绕点O旋转后的△DEF.
解:(1)三个特点:
①对应点到旋转中心的距离相等;
②任意一对对应点与旋转中心的连线所成的角相等;
③两个三角形全等.
(2)连接AD,BE,分别作线段AD与BE的垂直平分线,交于点O,O就是旋转中心.
连接OC,作∠COM=∠BOE,
再在OM上截取OF=OC,
连接EF,DF,即可得到旋转后的△DEF.
同课章节目录
