2021-2022学年人教版九年级数学上册23.1.2旋转性质的综合运用同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册23.1.2旋转性质的综合运用同步练习题 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 128.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 00:00:00 | ||
图片预览



文档简介
23.1.2旋转性质的综合运用同步练习题
2021-2022学年人教版九年级数学上册
01基础题
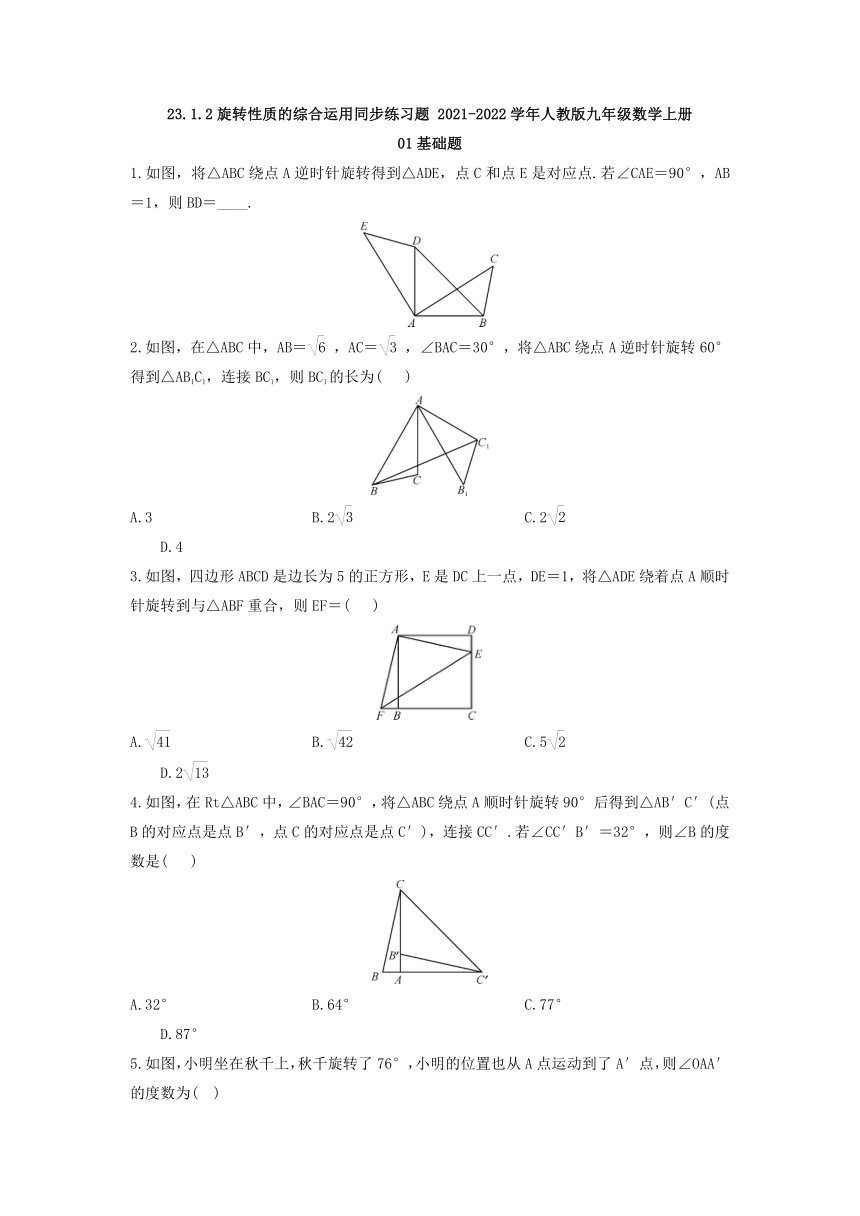
1.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=____.
2.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为(
)
A.3
B.2
C.2
D.4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=(
)
A.
B.
C.5
D.2
4.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的度数是(
)
A.32°
B.64°
C.77°
D.87°
5.如图,小明坐在秋千上,秋千旋转了76°,小明的位置也从A点运动到了A′点,则∠OAA′的度数为(
)
A.28°
B.52°
C.74°
D.76°
6.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(
)
A.1.6
B.1.8
C.2
D.2.6
7.如图,在△ABC中,∠CAB=62°,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为(
)
A.64°
B.52°
C.62°
D.56°
8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为(
)
A.18°
B.20°
C.24°
D.28°
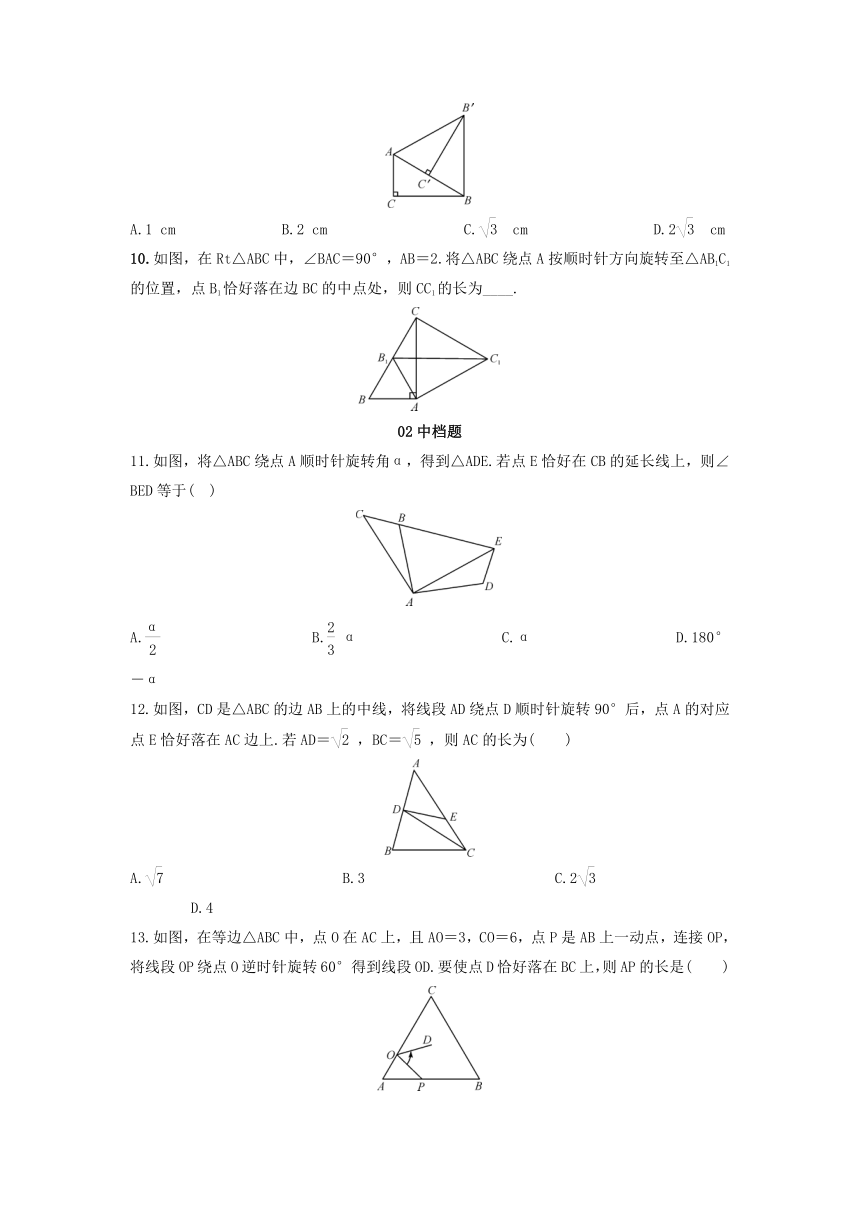
9.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1
cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是(
)
A.1
cm
B.2
cm
C.
cm
D.2
cm
10.如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为____.
02中档题
11.如图,将△ABC绕点A顺时针旋转角α,得到△ADE.若点E恰好在CB的延长线上,则∠BED等于(
)
A.
B.α
C.α
D.180°-α
12.如图,CD是△ABC的边AB上的中线,将线段AD绕点D顺时针旋转90°后,点A的对应点E恰好落在AC边上.若AD=,BC=,则AC的长为(
)
A.
B.3
C.2
D.4
13.如图,在等边△ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是(
)
A.4
B.5
C.6
D.8
14.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°得到△ADE.若AB=2,∠ACB=30°,则线段CD的长为____.
15.如图,在△ABC中,∠BAC=90°,AB=AC=10
cm,点D为△ABC内一点,∠BAD=15°,AD=6
cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为____cm.
03综合题
16.如图,已知等边△ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
(1)依题意补全图形.
(2)若OA=,OB=,OC=1,求∠OCM的度数.
参考答案
23.1.2旋转性质的综合运用同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=.
2.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为(A)
A.3
B.2
C.2
D.4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=(D)
A.
B.
C.5
D.2
4.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的度数是(C)
A.32°
B.64°
C.77°
D.87°
5.如图,小明坐在秋千上,秋千旋转了76°,小明的位置也从A点运动到了A′点,则∠OAA′的度数为(B)
A.28°
B.52°
C.74°
D.76°
6.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(A)
A.1.6
B.1.8
C.2
D.2.6
7.如图,在△ABC中,∠CAB=62°,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为(D)
A.64°
B.52°
C.62°
D.56°
8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为(C)
A.18°
B.20°
C.24°
D.28°
9.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1
cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是(B)
A.1
cm
B.2
cm
C.
cm
D.2
cm
10.如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为2.
02中档题
11.如图,将△ABC绕点A顺时针旋转角α,得到△ADE.若点E恰好在CB的延长线上,则∠BED等于(D)
A.
B.α
C.α
D.180°-α
12.如图,CD是△ABC的边AB上的中线,将线段AD绕点D顺时针旋转90°后,点A的对应点E恰好落在AC边上.若AD=,BC=,则AC的长为(B)
A.
B.3
C.2
D.4
13.如图,在等边△ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是(C)
A.4
B.5
C.6
D.8
14.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°得到△ADE.若AB=2,∠ACB=30°,则线段CD的长为2.
15.如图,在△ABC中,∠BAC=90°,AB=AC=10
cm,点D为△ABC内一点,∠BAD=15°,AD=6
cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为(10-2)cm.
03综合题
16.如图,已知等边△ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
(1)依题意补全图形.
(2)若OA=,OB=,OC=1,求∠OCM的度数.
解:(1)依题意补全图形,如图所示.
(2)连接OM.
∵△ABC为等边三角形,
∴∠ABC=60°.
∵△BAO绕点B旋转得到△BCM,OA=,OB=,
∴MC=OA=,MB=OB=,∠OBM=∠ABC=60°.
∴△OBM为等边三角形.
∴OM=OB=.
∵在△OMC中,OC=1,MC=,OM=,
∴OC2+MC2=OM2.
∴∠OCM=90°.
2021-2022学年人教版九年级数学上册
01基础题
1.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=____.
2.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为(
)
A.3
B.2
C.2
D.4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=(
)
A.
B.
C.5
D.2
4.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的度数是(
)
A.32°
B.64°
C.77°
D.87°
5.如图,小明坐在秋千上,秋千旋转了76°,小明的位置也从A点运动到了A′点,则∠OAA′的度数为(
)
A.28°
B.52°
C.74°
D.76°
6.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(
)
A.1.6
B.1.8
C.2
D.2.6
7.如图,在△ABC中,∠CAB=62°,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为(
)
A.64°
B.52°
C.62°
D.56°
8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为(
)
A.18°
B.20°
C.24°
D.28°
9.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1
cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是(
)
A.1
cm
B.2
cm
C.
cm
D.2
cm
10.如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为____.
02中档题
11.如图,将△ABC绕点A顺时针旋转角α,得到△ADE.若点E恰好在CB的延长线上,则∠BED等于(
)
A.
B.α
C.α
D.180°-α
12.如图,CD是△ABC的边AB上的中线,将线段AD绕点D顺时针旋转90°后,点A的对应点E恰好落在AC边上.若AD=,BC=,则AC的长为(
)
A.
B.3
C.2
D.4
13.如图,在等边△ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是(
)
A.4
B.5
C.6
D.8
14.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°得到△ADE.若AB=2,∠ACB=30°,则线段CD的长为____.
15.如图,在△ABC中,∠BAC=90°,AB=AC=10
cm,点D为△ABC内一点,∠BAD=15°,AD=6
cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为____cm.
03综合题
16.如图,已知等边△ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
(1)依题意补全图形.
(2)若OA=,OB=,OC=1,求∠OCM的度数.
参考答案
23.1.2旋转性质的综合运用同步练习题
2021-2022学年人教版九年级数学上册
01基础题
1.如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点.若∠CAE=90°,AB=1,则BD=.
2.如图,在△ABC中,AB=,AC=,∠BAC=30°,将△ABC绕点A逆时针旋转60°得到△AB1C1,连接BC1,则BC1的长为(A)
A.3
B.2
C.2
D.4
3.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕着点A顺时针旋转到与△ABF重合,则EF=(D)
A.
B.
C.5
D.2
4.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′.若∠CC′B′=32°,则∠B的度数是(C)
A.32°
B.64°
C.77°
D.87°
5.如图,小明坐在秋千上,秋千旋转了76°,小明的位置也从A点运动到了A′点,则∠OAA′的度数为(B)
A.28°
B.52°
C.74°
D.76°
6.如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A顺时针旋转得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为(A)
A.1.6
B.1.8
C.2
D.2.6
7.如图,在△ABC中,∠CAB=62°,将△ABC绕点A旋转到△AB′C′的位置,使得CC′∥AB,则∠BAB′的度数为(D)
A.64°
B.52°
C.62°
D.56°
8.如图,在△ABC中,∠BAC=108°,将△ABC绕点A按逆时针方向旋转得到△AB′C′.若点B′恰好落在BC边上,且AB′=CB′,则∠C′的度数为(C)
A.18°
B.20°
C.24°
D.28°
9.如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AC=1
cm,将Rt△ABC绕点A逆时针旋转得到Rt△AB′C′,使点C′落在AB边上,连接BB′,则BB′的长度是(B)
A.1
cm
B.2
cm
C.
cm
D.2
cm
10.如图,在Rt△ABC中,∠BAC=90°,AB=2.将△ABC绕点A按顺时针方向旋转至△AB1C1的位置,点B1恰好落在边BC的中点处,则CC1的长为2.
02中档题
11.如图,将△ABC绕点A顺时针旋转角α,得到△ADE.若点E恰好在CB的延长线上,则∠BED等于(D)
A.
B.α
C.α
D.180°-α
12.如图,CD是△ABC的边AB上的中线,将线段AD绕点D顺时针旋转90°后,点A的对应点E恰好落在AC边上.若AD=,BC=,则AC的长为(B)
A.
B.3
C.2
D.4
13.如图,在等边△ABC中,点O在AC上,且AO=3,CO=6,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转60°得到线段OD.要使点D恰好落在BC上,则AP的长是(C)
A.4
B.5
C.6
D.8
14.如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°得到△ADE.若AB=2,∠ACB=30°,则线段CD的长为2.
15.如图,在△ABC中,∠BAC=90°,AB=AC=10
cm,点D为△ABC内一点,∠BAD=15°,AD=6
cm,连接BD,将△ABD绕点A按逆时针方向旋转,使AB与AC重合,点D的对应点为点E,连接DE,DE交AC于点F,则CF的长为(10-2)cm.
03综合题
16.如图,已知等边△ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B旋转至△BCM.
(1)依题意补全图形.
(2)若OA=,OB=,OC=1,求∠OCM的度数.
解:(1)依题意补全图形,如图所示.
(2)连接OM.
∵△ABC为等边三角形,
∴∠ABC=60°.
∵△BAO绕点B旋转得到△BCM,OA=,OB=,
∴MC=OA=,MB=OB=,∠OBM=∠ABC=60°.
∴△OBM为等边三角形.
∴OM=OB=.
∵在△OMC中,OC=1,MC=,OM=,
∴OC2+MC2=OM2.
∴∠OCM=90°.
同课章节目录
