2021-2022学年人教版九年级数学上册22.3.3实物抛物线 同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册22.3.3实物抛物线 同步练习题 (word版含答案) | 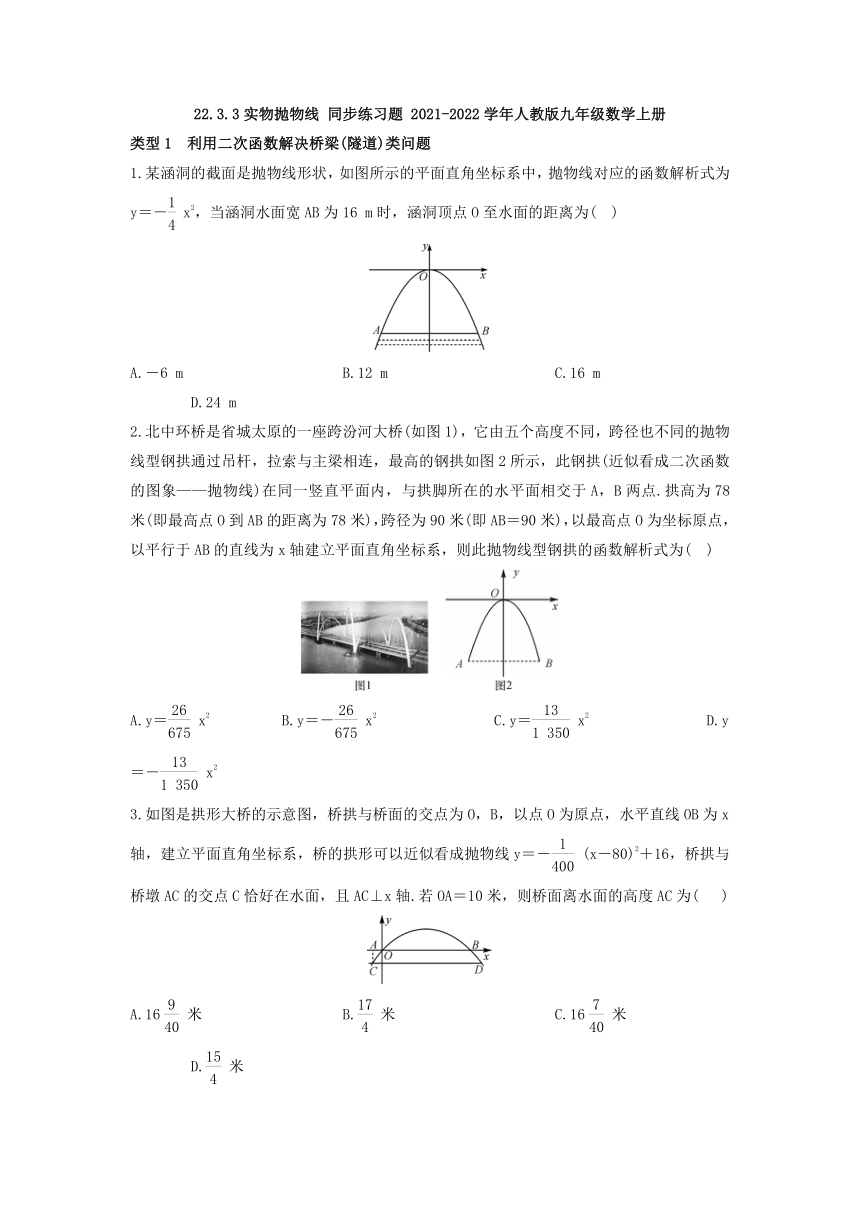 | |
| 格式 | docx | ||
| 文件大小 | 331.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:12:30 | ||
图片预览




文档简介
22.3.3实物抛物线
同步练习题
2021-2022学年人教版九年级数学上册
类型1 利用二次函数解决桥梁(隧道)类问题
1.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=-x2,当涵洞水面宽AB为16
m时,涵洞顶点O至水面的距离为(
)
A.-6
m
B.12
m
C.16
m
D.24
m
2.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数解析式为(
)
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
3.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,且AC⊥x轴.若OA=10米,则桥面离水面的高度AC为(
)
A.16米
B.米
C.16米
D.米
4.如图是抛物线型拱桥,当拱顶离水面2
m时,水面宽4
m,若水面下降2
m,则水面宽度增加______m.
5.如图,有一座抛物线型拱桥,桥下面在正常水位时AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示的平面直角坐标系中,求抛物线的解析式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
类型2 利用二次函数解决运动类问题
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(米)的一部分,则水喷出的最大高度是(
)
A.4米
B.3米
C.2米
D.1米
7.如图所示的是跳水运动员10
m跳台跳水的运动轨迹,运动员从10
m高A处的跳台上跳出,运动轨迹成抛物线状(抛物线所在平面与跳台墙面垂直).若运动员的最高点M离墙1
m,离水面
m,则运动员落水点B离墙的距离OB是(
)
A.2
m
B.3
m
C.4
m
D.5
m
8.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=40x-2x2,该型号飞机着陆后需滑行______m才能停下来.
9.随着新农村的建设和旧城的改造,我们的家园变得越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线型水柱在离水池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.
(1)请你建立适当的平面直角坐标系,并求出抛物线的函数解析式.
(2)求出水柱的最大高度.
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时.
①求h的值.
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
11.如图,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的平面直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m,到地面OA的距离为
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少米?
参考答案
22.3.3实物抛物线
同步练习题
2021-2022学年人教版九年级数学上册
类型1 利用二次函数解决桥梁(隧道)类问题
1.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=-x2,当涵洞水面宽AB为16
m时,涵洞顶点O至水面的距离为(C)
A.-6
m
B.12
m
C.16
m
D.24
m
2.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数解析式为(B)
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
3.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,且AC⊥x轴.若OA=10米,则桥面离水面的高度AC为(B)
A.16米
B.米
C.16米
D.米
4.如图是抛物线型拱桥,当拱顶离水面2
m时,水面宽4
m,若水面下降2
m,则水面宽度增加(4-4)m.
5.如图,有一座抛物线型拱桥,桥下面在正常水位时AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示的平面直角坐标系中,求抛物线的解析式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
解:(1)设所求抛物线的解析式为y=ax2(a≠0).
由CD=10
m,可设D(5,b).
∵AB=20
m,水位上升3
m就达到警戒线CD,
∴B(10,b-3).
把点D,B的坐标分别代入y=ax2,得
解得
∴y=-x2.
(2)∵b=-1,∴拱桥顶O到CD的距离为1
m.
∴=5(小时).
∴再持续5小时到达拱桥顶.
类型2 利用二次函数解决运动类问题
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(米)的一部分,则水喷出的最大高度是(A)
A.4米
B.3米
C.2米
D.1米
7.如图所示的是跳水运动员10
m跳台跳水的运动轨迹,运动员从10
m高A处的跳台上跳出,运动轨迹成抛物线状(抛物线所在平面与跳台墙面垂直).若运动员的最高点M离墙1
m,离水面
m,则运动员落水点B离墙的距离OB是(B)
A.2
m
B.3
m
C.4
m
D.5
m
8.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=40x-2x2,该型号飞机着陆后需滑行200m才能停下来.
9.随着新农村的建设和旧城的改造,我们的家园变得越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线型水柱在离水池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.
(1)请你建立适当的平面直角坐标系,并求出抛物线的函数解析式.
(2)求出水柱的最大高度.
解:(1)如图所示:以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+h,
代入(0,2)和(3,0),得
解得
∴抛物线的解析式为y=-(x-1)2+,
即y=-x2+x+2(0≤x≤3).
(2)∵y=-(x-1)2+(0≤x≤3),
∴当x=1时,y最大=.
答:水柱的最大高度为
m.
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时.
①求h的值.
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
解:(1)①当a=-时,y=-(x-4)2+h,
将点P(0,1)代入,得-×16+h=1,
解得h=.
②把x=5代入y=-(x-4)2+,得
y=-×(5-4)2+=1.625,
∵1.625>1.55,
∴此球能过网.
(2)把(0,1),(7,)代入y=a(x-4)2+h,得
解得
∴a=-.
11.如图,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的平面直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m,到地面OA的距离为
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少米?
解:(1)由题意,得点B的坐标为(0,4),点C的坐标为(3,),
∴
解得
∴该抛物线的函数关系式为y=-x2+2x+4.
∵y=-x2+2x+4=-(x-6)2+10,
∴拱顶D到地面OA的距离为10
m.
(2)当x=6+4=10时,y=-x2+2x+4=-×102+2×10+4=>6,
∴这辆货车能安全通过.
(3)当y=8时,-x2+2x+4=8,即x2-12x+24=0,∴x1=6+2,x2=6-2.
∴两排灯的水平距离最小是6+2-(6-2)=4(m).
同步练习题
2021-2022学年人教版九年级数学上册
类型1 利用二次函数解决桥梁(隧道)类问题
1.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=-x2,当涵洞水面宽AB为16
m时,涵洞顶点O至水面的距离为(
)
A.-6
m
B.12
m
C.16
m
D.24
m
2.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数解析式为(
)
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
3.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,且AC⊥x轴.若OA=10米,则桥面离水面的高度AC为(
)
A.16米
B.米
C.16米
D.米
4.如图是抛物线型拱桥,当拱顶离水面2
m时,水面宽4
m,若水面下降2
m,则水面宽度增加______m.
5.如图,有一座抛物线型拱桥,桥下面在正常水位时AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示的平面直角坐标系中,求抛物线的解析式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
类型2 利用二次函数解决运动类问题
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(米)的一部分,则水喷出的最大高度是(
)
A.4米
B.3米
C.2米
D.1米
7.如图所示的是跳水运动员10
m跳台跳水的运动轨迹,运动员从10
m高A处的跳台上跳出,运动轨迹成抛物线状(抛物线所在平面与跳台墙面垂直).若运动员的最高点M离墙1
m,离水面
m,则运动员落水点B离墙的距离OB是(
)
A.2
m
B.3
m
C.4
m
D.5
m
8.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=40x-2x2,该型号飞机着陆后需滑行______m才能停下来.
9.随着新农村的建设和旧城的改造,我们的家园变得越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线型水柱在离水池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.
(1)请你建立适当的平面直角坐标系,并求出抛物线的函数解析式.
(2)求出水柱的最大高度.
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时.
①求h的值.
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
11.如图,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的平面直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m,到地面OA的距离为
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少米?
参考答案
22.3.3实物抛物线
同步练习题
2021-2022学年人教版九年级数学上册
类型1 利用二次函数解决桥梁(隧道)类问题
1.某涵洞的截面是抛物线形状,如图所示的平面直角坐标系中,抛物线对应的函数解析式为y=-x2,当涵洞水面宽AB为16
m时,涵洞顶点O至水面的距离为(C)
A.-6
m
B.12
m
C.16
m
D.24
m
2.北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊杆,拉索与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象——抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点.拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为x轴建立平面直角坐标系,则此抛物线型钢拱的函数解析式为(B)
A.y=x2
B.y=-x2
C.y=x2
D.y=-x2
3.如图是拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,且AC⊥x轴.若OA=10米,则桥面离水面的高度AC为(B)
A.16米
B.米
C.16米
D.米
4.如图是抛物线型拱桥,当拱顶离水面2
m时,水面宽4
m,若水面下降2
m,则水面宽度增加(4-4)m.
5.如图,有一座抛物线型拱桥,桥下面在正常水位时AB宽20
m,水位上升3
m就达到警戒线CD,这时水面宽度为10
m.
(1)在如图所示的平面直角坐标系中,求抛物线的解析式.
(2)若洪水到来时,水位以每小时0.2
m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
解:(1)设所求抛物线的解析式为y=ax2(a≠0).
由CD=10
m,可设D(5,b).
∵AB=20
m,水位上升3
m就达到警戒线CD,
∴B(10,b-3).
把点D,B的坐标分别代入y=ax2,得
解得
∴y=-x2.
(2)∵b=-1,∴拱桥顶O到CD的距离为1
m.
∴=5(小时).
∴再持续5小时到达拱桥顶.
类型2 利用二次函数解决运动类问题
6.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(米)的一部分,则水喷出的最大高度是(A)
A.4米
B.3米
C.2米
D.1米
7.如图所示的是跳水运动员10
m跳台跳水的运动轨迹,运动员从10
m高A处的跳台上跳出,运动轨迹成抛物线状(抛物线所在平面与跳台墙面垂直).若运动员的最高点M离墙1
m,离水面
m,则运动员落水点B离墙的距离OB是(B)
A.2
m
B.3
m
C.4
m
D.5
m
8.某一型号飞机着陆后滑行的距离y(单位:m)与滑行时间x(单位:s)之间的函数关系式是y=40x-2x2,该型号飞机着陆后需滑行200m才能停下来.
9.随着新农村的建设和旧城的改造,我们的家园变得越来越美丽,小明家附近广场中央新修了一个圆形喷水池,在水池中心竖直安装了一根高为2
m的喷水管,它喷出的抛物线型水柱在离水池中心的水平距离为1
m处达到最高,水柱落地处离池中心3
m.
(1)请你建立适当的平面直角坐标系,并求出抛物线的函数解析式.
(2)求出水柱的最大高度.
解:(1)如图所示:以水管与地面交点为原点,原点与水柱落地点所在直线为x轴,水管所在直线为y轴,建立平面直角坐标系.
设抛物线的解析式为y=a(x-1)2+h,
代入(0,2)和(3,0),得
解得
∴抛物线的解析式为y=-(x-1)2+,
即y=-x2+x+2(0≤x≤3).
(2)∵y=-(x-1)2+(0≤x≤3),
∴当x=1时,y最大=.
答:水柱的最大高度为
m.
10.甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在O点正上方1
m的P处发出一球,羽毛球飞行的高度y(m)与水平距离x(m)之间满足函数解析式y=a(x-4)2+h,已知点O与球网的水平距离为5
m,球网的高度为1.55
m.
(1)当a=-时.
①求h的值.
②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到与点O的水平距离为7
m,离地面的高度为
m的Q处时,乙扣球成功,求a的值.
解:(1)①当a=-时,y=-(x-4)2+h,
将点P(0,1)代入,得-×16+h=1,
解得h=.
②把x=5代入y=-(x-4)2+,得
y=-×(5-4)2+=1.625,
∵1.625>1.55,
∴此球能过网.
(2)把(0,1),(7,)代入y=a(x-4)2+h,得
解得
∴a=-.
11.如图,隧道的截面由抛物线和长方形构成,长方形的长是12
m,宽是4
m.按照图中所示的平面直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到墙面OB的水平距离为3
m,到地面OA的距离为
m.
(1)求该抛物线的函数关系式,并计算出拱顶D到地面OA的距离.
(2)一辆货运汽车载一长方体集装箱后高为6
m,宽为4
m,如果隧道内设双向行车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等.如果灯离地面的高度不超过8
m,那么两排灯的水平距离最小是多少米?
解:(1)由题意,得点B的坐标为(0,4),点C的坐标为(3,),
∴
解得
∴该抛物线的函数关系式为y=-x2+2x+4.
∵y=-x2+2x+4=-(x-6)2+10,
∴拱顶D到地面OA的距离为10
m.
(2)当x=6+4=10时,y=-x2+2x+4=-×102+2×10+4=>6,
∴这辆货车能安全通过.
(3)当y=8时,-x2+2x+4=8,即x2-12x+24=0,∴x1=6+2,x2=6-2.
∴两排灯的水平距离最小是6+2-(6-2)=4(m).
同课章节目录
