12.3.1角的平分线的性质 同步练习题(Word版 含答案)2021-2022学年人教版八年级数学上册
文档属性
| 名称 | 12.3.1角的平分线的性质 同步练习题(Word版 含答案)2021-2022学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 142.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:24:18 | ||
图片预览



文档简介
12.3.1角的平分线的性质
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
一、选择题
1.如果要作∠AOB的平分线OC,合理的顺序是(
)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内部相交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角的平分线上的点到角的两边的距离相等
3.如图,已知△ABC,用尺规作图法作出∠ABC的平分线,保留作图痕迹,不写作法.
4.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是(B)
A.PC=PD
B.∠CPD=∠DOP
C.∠CPO=∠DPO
D.OC=OD
二、填空题
5.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为______.
6.命题“全等三角形对应边上的高相等”的已知是_________________,求证是______________________.
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,____________________.
求证:_____.
请你补全已知和求证,并写出证明过程.
B组(中档题)
一、选择题
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线.若CD=2,AB=6,则△ABD的面积是(
)
A.6
B.8
C.10
D.12
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
)
A.8
B.6
C.4
D.2
二、填空题
10.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠ADC的度数为_____.
11.如图,在四边形ABCD中,∠A=90°,AD=5,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长度的最小值为_____.
12.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留作图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC;
(2)连接AE,DC,两边交于点P;
(3)作射线OP;
(4)求证:OP平分∠MON.
13.求证:有两个角及其中一个角的平分线对应相等的两个三角形全等.
C组(综合题)
14.已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
参考答案
12.3.1角的平分线的性质
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如果要作∠AOB的平分线OC,合理的顺序是(C)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内部相交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(A)
A.SSS
B.ASA
C.AAS
D.角的平分线上的点到角的两边的距离相等
3.如图,已知△ABC,用尺规作图法作出∠ABC的平分线,保留作图痕迹,不写作法.
解:如图所示.
4.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是(B)
A.PC=PD
B.∠CPD=∠DOP
C.∠CPO=∠DPO
D.OC=OD
5.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为3.
6.命题“全等三角形对应边上的高相等”的已知是两条线段是两个全等三角形对应边上的高,求证是这两条线段相等.
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
请你补全已知和求证,并写出证明过程.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).
∴PD=PE.
B组(中档题)
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线.若CD=2,AB=6,则△ABD的面积是(A)
A.6
B.8
C.10
D.12
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(C)
A.8
B.6
C.4
D.2
10.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠ADC的度数为65°.
11.如图,在四边形ABCD中,∠A=90°,AD=5,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长度的最小值为5.
12.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留作图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC;
(2)连接AE,DC,两边交于点P;
(3)作射线OP;
(4)求证:OP平分∠MON.
解:(1)(2)(3)如图所示.
(4)证明:在△DOC和△AOE中,
∴△DOC≌△AOE(SAS).
∴∠OCD=∠OEA.
∵OD=OA,OE=OC,
∴OE-OD=OC-OA,即DE=AC.
在△APC和△DPE中,
∴△APC≌△DPE(AAS).
∴CP=EP.
在△POC和△POE中,
∴△POC≌△POE(SSS).
∴∠COP=∠EOP,即OP平分∠MON.
13.求证:有两个角及其中一个角的平分线对应相等的两个三角形全等.
解:已知:如图,在△ABC和△A′B′C′中,∠B=∠B′,∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,且AD=A′D′.
求证:△ABC≌△A′B′C′.
证明:∵∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,
∴∠BAD=∠B′A′D′.
在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(AAS).
∴AB=A′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
C组(综合题)
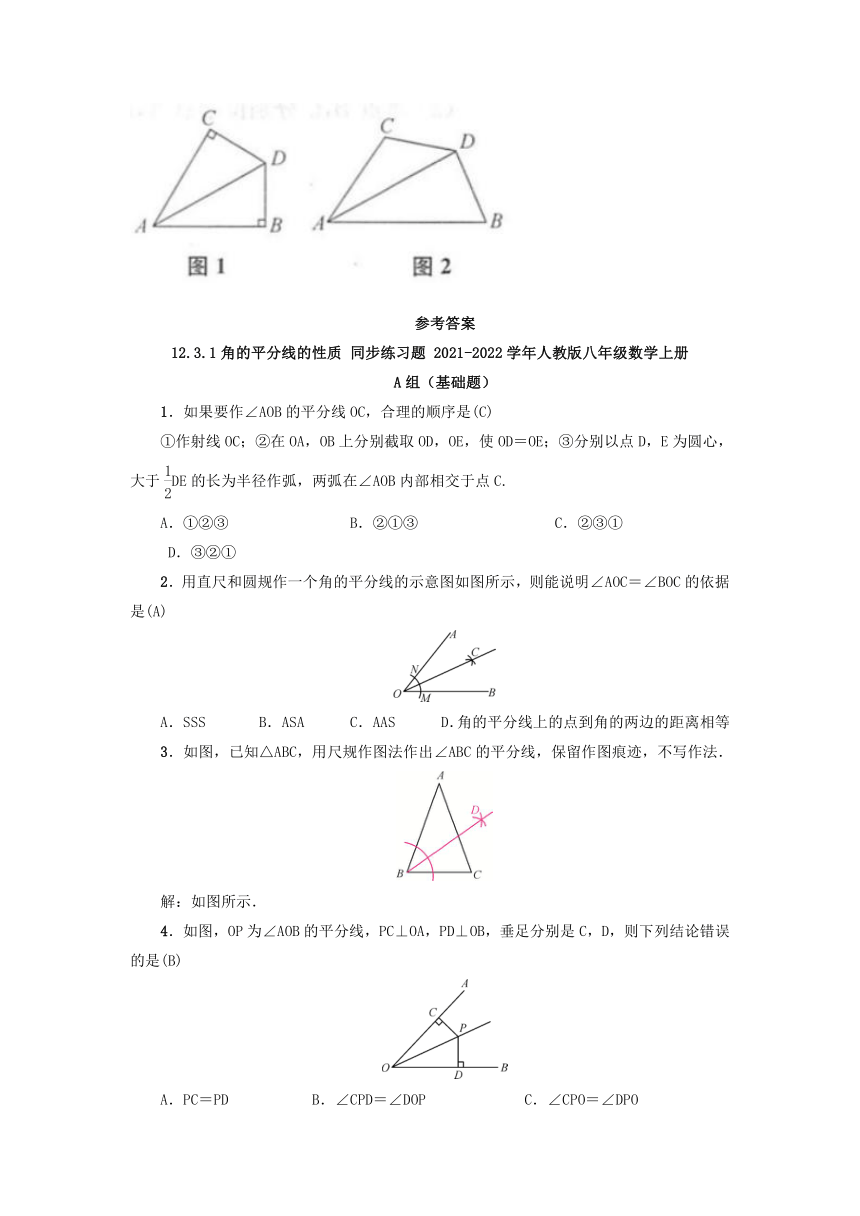
14.已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
证明:过点D分别作DE⊥AB于点E,DF⊥AC于点F,则∠DFC=∠DEB=90°.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).
∴DB=DC.
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
一、选择题
1.如果要作∠AOB的平分线OC,合理的顺序是(
)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内部相交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(
)
A.SSS
B.ASA
C.AAS
D.角的平分线上的点到角的两边的距离相等
3.如图,已知△ABC,用尺规作图法作出∠ABC的平分线,保留作图痕迹,不写作法.
4.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是(B)
A.PC=PD
B.∠CPD=∠DOP
C.∠CPO=∠DPO
D.OC=OD
二、填空题
5.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为______.
6.命题“全等三角形对应边上的高相等”的已知是_________________,求证是______________________.
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,____________________.
求证:_____.
请你补全已知和求证,并写出证明过程.
B组(中档题)
一、选择题
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线.若CD=2,AB=6,则△ABD的面积是(
)
A.6
B.8
C.10
D.12
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(
)
A.8
B.6
C.4
D.2
二、填空题
10.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠ADC的度数为_____.
11.如图,在四边形ABCD中,∠A=90°,AD=5,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长度的最小值为_____.
12.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留作图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC;
(2)连接AE,DC,两边交于点P;
(3)作射线OP;
(4)求证:OP平分∠MON.
13.求证:有两个角及其中一个角的平分线对应相等的两个三角形全等.
C组(综合题)
14.已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
参考答案
12.3.1角的平分线的性质
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如果要作∠AOB的平分线OC,合理的顺序是(C)
①作射线OC;②在OA,OB上分别截取OD,OE,使OD=OE;③分别以点D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB内部相交于点C.
A.①②③
B.②①③
C.②③①
D.③②①
2.用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是(A)
A.SSS
B.ASA
C.AAS
D.角的平分线上的点到角的两边的距离相等
3.如图,已知△ABC,用尺规作图法作出∠ABC的平分线,保留作图痕迹,不写作法.
解:如图所示.
4.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,则下列结论错误的是(B)
A.PC=PD
B.∠CPD=∠DOP
C.∠CPO=∠DPO
D.OC=OD
5.如图,点P是∠AOC的平分线上一点,PD⊥OA,垂足为D,且PD=3,点M是射线OC上一动点,则PM的最小值为3.
6.命题“全等三角形对应边上的高相等”的已知是两条线段是两个全等三角形对应边上的高,求证是这两条线段相等.
7.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D,E.
求证:PD=PE.
请你补全已知和求证,并写出证明过程.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).
∴PD=PE.
B组(中档题)
8.如图,在△ABC中,∠C=90°,AD是∠BAC的平分线.若CD=2,AB=6,则△ABD的面积是(A)
A.6
B.8
C.10
D.12
9.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是(C)
A.8
B.6
C.4
D.2
10.如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB,AC于点E,F;②分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D,则∠ADC的度数为65°.
11.如图,在四边形ABCD中,∠A=90°,AD=5,连接BD,BD⊥CD,∠ADB=∠C.若P是边BC上一动点,则DP长度的最小值为5.
12.如图,已知∠MON,点A,C在射线OM上,请按要求完成下列作图(保留作图痕迹)及证明.
(1)在射线ON上分别截取OD=OA,OE=OC;
(2)连接AE,DC,两边交于点P;
(3)作射线OP;
(4)求证:OP平分∠MON.
解:(1)(2)(3)如图所示.
(4)证明:在△DOC和△AOE中,
∴△DOC≌△AOE(SAS).
∴∠OCD=∠OEA.
∵OD=OA,OE=OC,
∴OE-OD=OC-OA,即DE=AC.
在△APC和△DPE中,
∴△APC≌△DPE(AAS).
∴CP=EP.
在△POC和△POE中,
∴△POC≌△POE(SSS).
∴∠COP=∠EOP,即OP平分∠MON.
13.求证:有两个角及其中一个角的平分线对应相等的两个三角形全等.
解:已知:如图,在△ABC和△A′B′C′中,∠B=∠B′,∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,且AD=A′D′.
求证:△ABC≌△A′B′C′.
证明:∵∠BAC=∠B′A′C′,AD,A′D′分别是∠BAC,∠B′A′C′的平分线,
∴∠BAD=∠B′A′D′.
在△ABD和△A′B′D′中,
∴△ABD≌△A′B′D′(AAS).
∴AB=A′B′.
在△ABC和△A′B′C′中,
∴△ABC≌△A′B′C′(ASA).
C组(综合题)
14.已知:如图1,AD平分∠BAC,∠B+∠C=180°,∠B=90°.易知:DB=DC.
探究:如图2,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°.求证:DB=DC.
证明:过点D分别作DE⊥AB于点E,DF⊥AC于点F,则∠DFC=∠DEB=90°.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
在△DFC和△DEB中,
∴△DFC≌△DEB(AAS).
∴DB=DC.
