14.2.1平方差公式同步练习题 2021-2022学年人教版八年级数学上册(Word版 含答案)
文档属性
| 名称 | 14.2.1平方差公式同步练习题 2021-2022学年人教版八年级数学上册(Word版 含答案) | 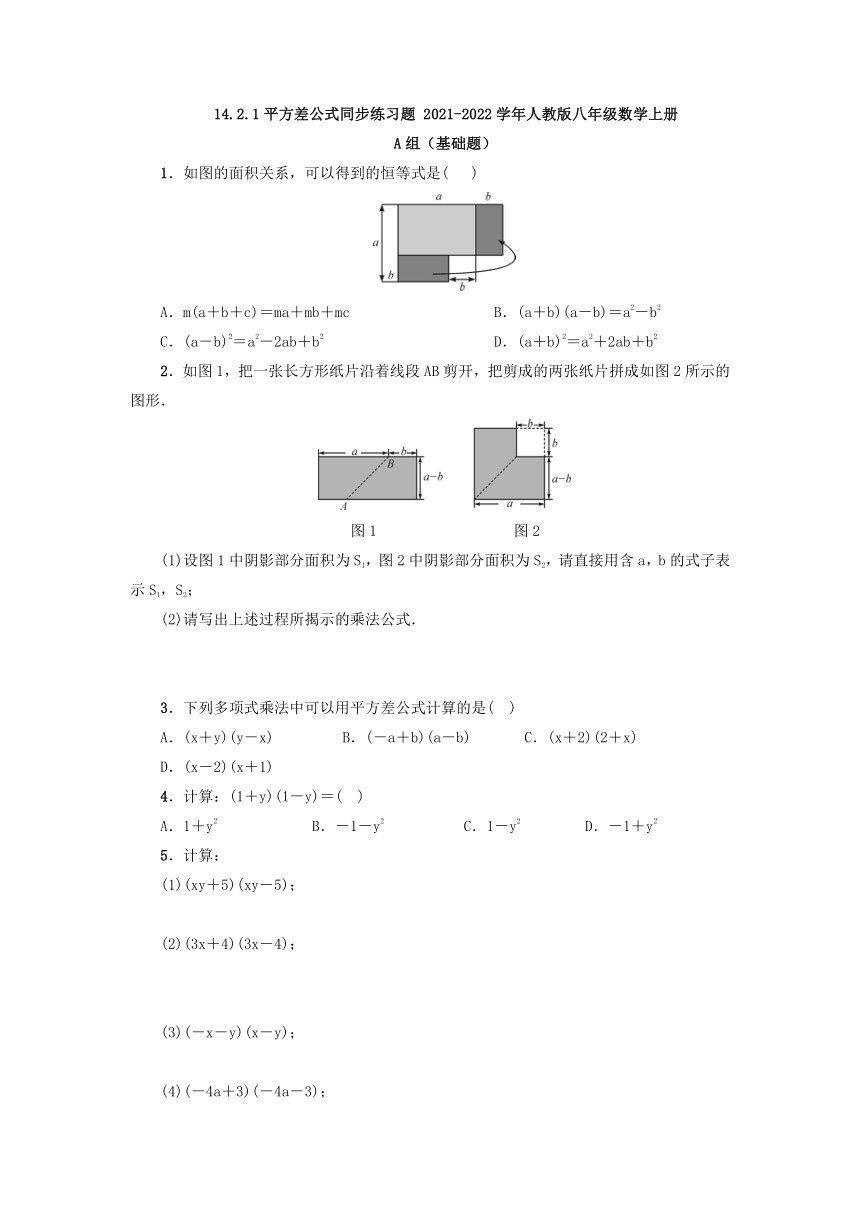 | |
| 格式 | docx | ||
| 文件大小 | 48.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:29:11 | ||
图片预览



文档简介
14.2.1平方差公式同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图的面积关系,可以得到的恒等式是(
)
A.m(a+b+c)=ma+mb+mc
B.(a+b)(a-b)=a2-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
2.如图1,把一张长方形纸片沿着线段AB剪开,把剪成的两张纸片拼成如图2所示的图形.
图1 图2
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
3.下列多项式乘法中可以用平方差公式计算的是(
)
A.(x+y)(y-x)
B.(-a+b)(a-b)
C.(x+2)(2+x)
D.(x-2)(x+1)
4.计算:(1+y)(1-y)=(
)
A.1+y2
B.-1-y2
C.1-y2
D.-1+y2
5.计算:
(1)(xy+5)(xy-5);
(2)(3x+4)(3x-4);
(3)(-x-y)(x-y);
(4)(-4a+3)(-4a-3);
(5)b(a+b)+(a+b)(a-b).
6.运用平方差公式计算:52×48=(___+___)×(___-___)=___-___=___-___=___.
7.定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x-1)※x的结果为___.
8.运用平方差公式进行简便计算:
(1)10×9;
(2)9.8×10.2;
(3)1
007×993.
9.下列计算正确的是(
)
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a+3b)=a2-9b2
B组(中档题)
10.若M·(3x-y2)=y4-9x2,则M为(
)
A.-3x-y2
B.-3x+y2
C.3x+y2
D.3x-y2
11.对于任意正整数n,能整除式子(3n+1)(3n-1)-(3-n)(3+n)的整数是(
)
A.3
B.6
C.10
D.9
12.如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为___.
13.若(m+n-1)(m+1+n)=80,则m+n=___;
14.若(a2+b2+1)(a2+b2-1)-3=0,则a2+b2=___.
15.计算:
(1)(5m+2)(5m-2)-(3m+1)(2m-1);
(2)2019×2
021-2
0202.
16.(1)先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
(2)已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
17.某中学为了响应国家“发展体育运动,增强人民体质”的号召,决定建一个长方体游泳池,已知游泳池长为(4a2+9b2)m,宽为(2a+3b)m,深为(2a-3b)m,则这个游泳池的容积是多少?
C组(综合题)
18.先观察下面的解题过程,然后解答问题:
化简:(2+1)(22+1)(24+1).
解:原式=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=28-1.
化简:(3+1)(32+1)(34+1)(38+1)…(364+1).
参考答案
14.2.1平方差公式同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图的面积关系,可以得到的恒等式是(B)
A.m(a+b+c)=ma+mb+mc
B.(a+b)(a-b)=a2-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
2.如图1,把一张长方形纸片沿着线段AB剪开,把剪成的两张纸片拼成如图2所示的图形.
图1 图2
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
解:(1)S1=(a+b)(a-b),
S2=a2-b2.
(2)(a+b)(a-b)=a2-b2.
3.下列多项式乘法中可以用平方差公式计算的是(A)
A.(x+y)(y-x)
B.(-a+b)(a-b)
C.(x+2)(2+x)
D.(x-2)(x+1)
4.计算:(1+y)(1-y)=(C)
A.1+y2
B.-1-y2
C.1-y2
D.-1+y2
5.计算:
(1)(xy+5)(xy-5);
解:原式=x2y2-25.
(2)(3x+4)(3x-4);
解:原式=9x2-16.
(3)(-x-y)(x-y);
解:原式=(-y)2-x2=y2-x2.
(4)(-4a+3)(-4a-3);
解:原式=(-4a)2-32=16a2-9.
(5)b(a+b)+(a+b)(a-b).
解:原式=ab+b2+a2-b2
=ab+a2.
6.运用平方差公式计算:52×48=(50+2)×(50-2)=502-22=2_500-4=2_496.
7.定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x-1)※x的结果为x2-1.
8.运用平方差公式进行简便计算:
(1)10×9;
解:原式=(10+)(10-)
=102-()2
=100-
=99.
(2)9.8×10.2;
解:原式=(10-0.2)×(10+0.2)
=102-0.22
=100-0.04
=99.96.
(3)1
007×993.
解:原式=(1
000+7)×(1
000-7)
=1
0002-72
=999
951.
9.下列计算正确的是(C)
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a+3b)=a2-9b2
B组(中档题)
10.若M·(3x-y2)=y4-9x2,则M为(A)
A.-3x-y2
B.-3x+y2
C.3x+y2
D.3x-y2
11.对于任意正整数n,能整除式子(3n+1)(3n-1)-(3-n)(3+n)的整数是(C)
A.3
B.6
C.10
D.9
12.如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为±1.
13.若(m+n-1)(m+1+n)=80,则m+n=±9;
14.若(a2+b2+1)(a2+b2-1)-3=0,则a2+b2=2.
15.计算:
(1)(5m+2)(5m-2)-(3m+1)(2m-1);
解:原式=(25m2-4)-(6m2-3m+2m-1)
=25m2-4-6m2+m+1
=19m2+m-3.
(2)2
019×2
021-2
0202.
解:原式=(2
020-1)×(2
020+1)-2
0202
=2
0202-1-2
0202
=-1.
16.(1)先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
原式=5×12-5×22=5-20=-15.
(2)已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
解:原式=9x2-4+x2-2x
=10x2-2x-4.
因为5x2-x-1=0,
所以5x2-x=1.
所以10x2-2x=2.
所以原式=2-4=-2.
17.某中学为了响应国家“发展体育运动,增强人民体质”的号召,决定建一个长方体游泳池,已知游泳池长为(4a2+9b2)m,宽为(2a+3b)m,深为(2a-3b)m,则这个游泳池的容积是多少?
解:(4a2+9b2)(2a+3b)(2a-3b)
=(4a2+9b2)(4a2-9b2)
=16a4-81b4.
答:这个游泳池的容积是(16a4-81b4)m3.
C组(综合题)
18.先观察下面的解题过程,然后解答问题:
化简:(2+1)(22+1)(24+1).
解:原式=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=28-1.
化简:(3+1)(32+1)(34+1)(38+1)…(364+1).
解:原式=(3-1)(3+1)(32+1)(34+1)(38+1)…(364+1)
=(32-1)(32+1)(34+1)(38+1)…(364+1)
=(34-1)(34+1)(38+1)…(364+1)
=(38-1)(38+1)…(364+1)
=(364-1)(364+1)
=(3128-1).
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图的面积关系,可以得到的恒等式是(
)
A.m(a+b+c)=ma+mb+mc
B.(a+b)(a-b)=a2-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
2.如图1,把一张长方形纸片沿着线段AB剪开,把剪成的两张纸片拼成如图2所示的图形.
图1 图2
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
3.下列多项式乘法中可以用平方差公式计算的是(
)
A.(x+y)(y-x)
B.(-a+b)(a-b)
C.(x+2)(2+x)
D.(x-2)(x+1)
4.计算:(1+y)(1-y)=(
)
A.1+y2
B.-1-y2
C.1-y2
D.-1+y2
5.计算:
(1)(xy+5)(xy-5);
(2)(3x+4)(3x-4);
(3)(-x-y)(x-y);
(4)(-4a+3)(-4a-3);
(5)b(a+b)+(a+b)(a-b).
6.运用平方差公式计算:52×48=(___+___)×(___-___)=___-___=___-___=___.
7.定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x-1)※x的结果为___.
8.运用平方差公式进行简便计算:
(1)10×9;
(2)9.8×10.2;
(3)1
007×993.
9.下列计算正确的是(
)
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a+3b)=a2-9b2
B组(中档题)
10.若M·(3x-y2)=y4-9x2,则M为(
)
A.-3x-y2
B.-3x+y2
C.3x+y2
D.3x-y2
11.对于任意正整数n,能整除式子(3n+1)(3n-1)-(3-n)(3+n)的整数是(
)
A.3
B.6
C.10
D.9
12.如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为___.
13.若(m+n-1)(m+1+n)=80,则m+n=___;
14.若(a2+b2+1)(a2+b2-1)-3=0,则a2+b2=___.
15.计算:
(1)(5m+2)(5m-2)-(3m+1)(2m-1);
(2)2019×2
021-2
0202.
16.(1)先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
(2)已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
17.某中学为了响应国家“发展体育运动,增强人民体质”的号召,决定建一个长方体游泳池,已知游泳池长为(4a2+9b2)m,宽为(2a+3b)m,深为(2a-3b)m,则这个游泳池的容积是多少?
C组(综合题)
18.先观察下面的解题过程,然后解答问题:
化简:(2+1)(22+1)(24+1).
解:原式=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=28-1.
化简:(3+1)(32+1)(34+1)(38+1)…(364+1).
参考答案
14.2.1平方差公式同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图的面积关系,可以得到的恒等式是(B)
A.m(a+b+c)=ma+mb+mc
B.(a+b)(a-b)=a2-b2
C.(a-b)2=a2-2ab+b2
D.(a+b)2=a2+2ab+b2
2.如图1,把一张长方形纸片沿着线段AB剪开,把剪成的两张纸片拼成如图2所示的图形.
图1 图2
(1)设图1中阴影部分面积为S1,图2中阴影部分面积为S2,请直接用含a,b的式子表示S1,S2;
(2)请写出上述过程所揭示的乘法公式.
解:(1)S1=(a+b)(a-b),
S2=a2-b2.
(2)(a+b)(a-b)=a2-b2.
3.下列多项式乘法中可以用平方差公式计算的是(A)
A.(x+y)(y-x)
B.(-a+b)(a-b)
C.(x+2)(2+x)
D.(x-2)(x+1)
4.计算:(1+y)(1-y)=(C)
A.1+y2
B.-1-y2
C.1-y2
D.-1+y2
5.计算:
(1)(xy+5)(xy-5);
解:原式=x2y2-25.
(2)(3x+4)(3x-4);
解:原式=9x2-16.
(3)(-x-y)(x-y);
解:原式=(-y)2-x2=y2-x2.
(4)(-4a+3)(-4a-3);
解:原式=(-4a)2-32=16a2-9.
(5)b(a+b)+(a+b)(a-b).
解:原式=ab+b2+a2-b2
=ab+a2.
6.运用平方差公式计算:52×48=(50+2)×(50-2)=502-22=2_500-4=2_496.
7.定义a※b=a(b+1),例如2※3=2×(3+1)=2×4=8.则(x-1)※x的结果为x2-1.
8.运用平方差公式进行简便计算:
(1)10×9;
解:原式=(10+)(10-)
=102-()2
=100-
=99.
(2)9.8×10.2;
解:原式=(10-0.2)×(10+0.2)
=102-0.22
=100-0.04
=99.96.
(3)1
007×993.
解:原式=(1
000+7)×(1
000-7)
=1
0002-72
=999
951.
9.下列计算正确的是(C)
A.(a+3b)(a-3b)=a2-3b2
B.(-a+3b)(a-3b)=-a2-9b2
C.(-a-3b)(a-3b)=-a2+9b2
D.(-a-3b)(a+3b)=a2-9b2
B组(中档题)
10.若M·(3x-y2)=y4-9x2,则M为(A)
A.-3x-y2
B.-3x+y2
C.3x+y2
D.3x-y2
11.对于任意正整数n,能整除式子(3n+1)(3n-1)-(3-n)(3+n)的整数是(C)
A.3
B.6
C.10
D.9
12.如果(2a+2b+1)(2a+2b-1)=3,那么a+b的值为±1.
13.若(m+n-1)(m+1+n)=80,则m+n=±9;
14.若(a2+b2+1)(a2+b2-1)-3=0,则a2+b2=2.
15.计算:
(1)(5m+2)(5m-2)-(3m+1)(2m-1);
解:原式=(25m2-4)-(6m2-3m+2m-1)
=25m2-4-6m2+m+1
=19m2+m-3.
(2)2
019×2
021-2
0202.
解:原式=(2
020-1)×(2
020+1)-2
0202
=2
0202-1-2
0202
=-1.
16.(1)先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2;
解:原式=4x2-y2-(4y2-x2)
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
原式=5×12-5×22=5-20=-15.
(2)已知5x2-x-1=0,求代数式(3x+2)(3x-2)+x(x-2)的值.
解:原式=9x2-4+x2-2x
=10x2-2x-4.
因为5x2-x-1=0,
所以5x2-x=1.
所以10x2-2x=2.
所以原式=2-4=-2.
17.某中学为了响应国家“发展体育运动,增强人民体质”的号召,决定建一个长方体游泳池,已知游泳池长为(4a2+9b2)m,宽为(2a+3b)m,深为(2a-3b)m,则这个游泳池的容积是多少?
解:(4a2+9b2)(2a+3b)(2a-3b)
=(4a2+9b2)(4a2-9b2)
=16a4-81b4.
答:这个游泳池的容积是(16a4-81b4)m3.
C组(综合题)
18.先观察下面的解题过程,然后解答问题:
化简:(2+1)(22+1)(24+1).
解:原式=(2-1)(2+1)(22+1)(24+1)
=(22-1)(22+1)(24+1)
=(24-1)(24+1)
=28-1.
化简:(3+1)(32+1)(34+1)(38+1)…(364+1).
解:原式=(3-1)(3+1)(32+1)(34+1)(38+1)…(364+1)
=(32-1)(32+1)(34+1)(38+1)…(364+1)
=(34-1)(34+1)(38+1)…(364+1)
=(38-1)(38+1)…(364+1)
=(364-1)(364+1)
=(3128-1).
