2021-2022学年人教版九年级数学上册21.3 实际问题与一元二次方程 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册21.3 实际问题与一元二次方程 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 68.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-04 10:42:58 | ||
图片预览




文档简介
21.3
实际问题与一元二次方程
同步练习题
2021-2022学年人教版九年级数学上册第21章
一、选择题
1.秋冬季节为流感的高发期,有1人患了流感,经过两轮传染后共有81人患了流感.设每轮传染中平均一个人传染x个人,则所列方程正确的是(
)
A.x(x-1)=81
B.x(x+1)=81
C.(x-1)2=81
D.(1+x)2=81
2.某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程(
)
A.(x+1)2=43
B.x+2x+1=43
C.x2+x+1=43
D.x(x+1)=43
3.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元.若二月份到四月份每个月的月营业额增长率都相同,设增长率为x,根据题意可列方程(
)
A.82(1+x)2=82(1+x)+20
B.82(1+x)2=82(1+x)
C.82(1+x)2=82+20
D.82(1+x)=82+20
4.在一次九年级学生数学交流会上,每两名学生握手一次,统计共握手253次.若设参加此会的学生为x名,则可列方程为(
)
A.x(x+1)=253
B.x(x-1)=253
C.x(x+1)=253
D.x(x-1)=253
5.如图,把小圆形场地的半径增加5
m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为(
)
A.5
m
B.(5+)m
C.(5+3)m
D.(5+5)m
二、填空题
6.有1个人得流感病,第一轮传染6个人,第一轮过后共有7人得流感,第二轮传染时平均每人也传染6人,第二轮被传染了______人,第二轮过后共有______人得流感.
7.春节期间,某微信群规定,群内每个人都要发一个红包,并保证群内其他人都能抢到,且自己不能抢自己发的红包,此次抢红包活动中,群内所有人共收到90个红包.若设该群一共有x人,则可列方程为______.
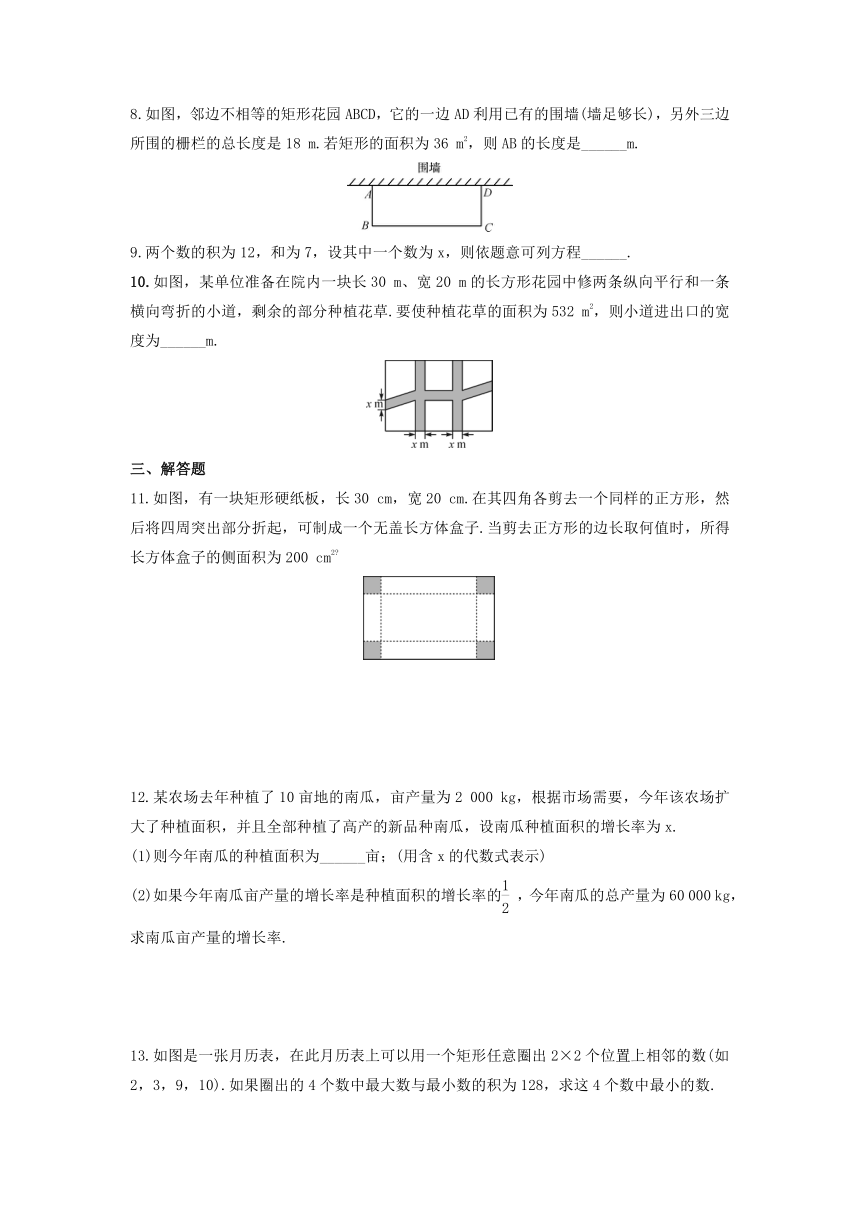
8.如图,邻边不相等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18
m.若矩形的面积为36
m2,则AB的长度是______m.
9.两个数的积为12,和为7,设其中一个数为x,则依题意可列方程______.
10.如图,某单位准备在院内一块长30
m、宽20
m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的部分种植花草.要使种植花草的面积为532
m2,则小道进出口的宽度为______m.
三、解答题
11.如图,有一块矩形硬纸板,长30
cm,宽20
cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200
cm2?
12.某农场去年种植了10亩地的南瓜,亩产量为2
000
kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为______亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的,今年南瓜的总产量为60
000
kg,求南瓜亩产量的增长率.
13.如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,求这4个数中最小的数.
14.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·为政》
读诗词解题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
15.如图1,某小区的平面图是一个占地长500米,宽400米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形,如果要使四周的空地所占面积是小区面积的19%,南北空地等宽,东西空地等宽.
(1)求该小区四周的空地的宽度.
(2)如图2,该小区在东、西、南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东、西两侧绿化带完全相同,其长均为200米,南侧绿化带的长为300米,绿化总面积为12
500平方米,请算出小区道路的宽度.
16.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率.
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,学校图书馆能否接纳第四个月的进馆人次,并说明理由.
17.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万千克与3.6万千克,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万千克.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
18.如图,在△ABC中,∠C=90°,AC=16
cm,BC=8
cm,一动点P从点C出发沿着CB边以2
cm/s的速度运动,另一动点Q从点A出发沿着AC边以4
cm/s的速度运动,P,Q两点同时出发,运动时间为t
s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
参考答案
21.3
实际问题与一元二次方程
同步练习题
2021-2022学年人教版九年级数学上册第21章
一、选择题
1.秋冬季节为流感的高发期,有1人患了流感,经过两轮传染后共有81人患了流感.设每轮传染中平均一个人传染x个人,则所列方程正确的是(D)
A.x(x-1)=81
B.x(x+1)=81
C.(x-1)2=81
D.(1+x)2=81
2.某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程(C)
A.(x+1)2=43
B.x+2x+1=43
C.x2+x+1=43
D.x(x+1)=43
3.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元.若二月份到四月份每个月的月营业额增长率都相同,设增长率为x,根据题意可列方程(A)
A.82(1+x)2=82(1+x)+20
B.82(1+x)2=82(1+x)
C.82(1+x)2=82+20
D.82(1+x)=82+20
4.在一次九年级学生数学交流会上,每两名学生握手一次,统计共握手253次.若设参加此会的学生为x名,则可列方程为(D)
A.x(x+1)=253
B.x(x-1)=253
C.x(x+1)=253
D.x(x-1)=253
5.如图,把小圆形场地的半径增加5
m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为(D)
A.5
m
B.(5+)m
C.(5+3)m
D.(5+5)m
二、填空题
6.有1个人得流感病,第一轮传染6个人,第一轮过后共有7人得流感,第二轮传染时平均每人也传染6人,第二轮被传染了42人,第二轮过后共有49人得流感.
7.春节期间,某微信群规定,群内每个人都要发一个红包,并保证群内其他人都能抢到,且自己不能抢自己发的红包,此次抢红包活动中,群内所有人共收到90个红包.若设该群一共有x人,则可列方程为x(x-1)=90.
8.如图,邻边不相等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18
m.若矩形的面积为36
m2,则AB的长度是3m.
9.两个数的积为12,和为7,设其中一个数为x,则依题意可列方程x2-7x+12=0.
10.如图,某单位准备在院内一块长30
m、宽20
m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的部分种植花草.要使种植花草的面积为532
m2,则小道进出口的宽度为1m.
三、解答题
11.如图,有一块矩形硬纸板,长30
cm,宽20
cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200
cm2?
解:设剪去正方形的边长为x
cm,则做成无盖长方体盒子的底面长为(30-2x)cm,宽为(20-2x)cm,高为x
cm,
依题意,得2×[(30-2x)+(20-2x)]x=200.
解得x1=,x2=10.
当x=10时,20-2x=0,
故x=10不合题意,应舍去.
答:当剪去正方形的边长为
cm时,所得长方体盒子的侧面积为200
cm2.
12.某农场去年种植了10亩地的南瓜,亩产量为2
000
kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为10(1+x)亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的,今年南瓜的总产量为60
000
kg,求南瓜亩产量的增长率.
解:根据题意,得10(1+x)×2
000(1+)=60
000,
整理,得x2+3x-4=0,
解得x1=1=100%,x2=-4(不合题意,舍去).
∴x=50%.
答:南瓜亩产量的增长率为50%.
13.如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,求这4个数中最小的数.
解:设这4个数中最小的数是x,则最大的数是x+8,根据题意,得
x(x+8)=128,
整理,得x2+8x-128=0.
解得x1=8,x2=-16(不合题意,舍去).
答:这4个数中最小的数是8.
14.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·为政》
读诗词解题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
解:设周瑜逝世的年龄的个位数字为x,则十位数字为x-3,根据题意,得
10(x-3)+x=x2,
解得x1=5,x2=6.
当x=5时,周瑜的年龄是25岁,
∵而立之年为30岁,25<30,
∴x=5不符合题意,应舍去;
当x=6时,周瑜的年龄是36岁,符合题意.
答:周瑜的年龄是36岁.
15.如图1,某小区的平面图是一个占地长500米,宽400米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形,如果要使四周的空地所占面积是小区面积的19%,南北空地等宽,东西空地等宽.
(1)求该小区四周的空地的宽度.
(2)如图2,该小区在东、西、南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东、西两侧绿化带完全相同,其长均为200米,南侧绿化带的长为300米,绿化总面积为12
500平方米,请算出小区道路的宽度.
解:(1)建筑区的面积是500×400×(1-19%)=162
000(平方米).
设建筑区的长度为5x米,则宽为4x米.根据题意,得5x·4x=162
000,整理,得x2=8
100.
解得x1=90,x2=-90(不合题意).
∴东西两侧道宽:(500-5x)÷2=25(米),
南北两侧道宽:(400-4x)÷2=20(米).
答:小区的东西两侧空地的宽度为25米,南北两侧空地的宽度为20米.
(2)设小区道路的宽度为z米,则
(20-z)×300+2×(25-z)×200=12
500.
解得z=5.
答:小区道路的宽度是5米.
16.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率.
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,学校图书馆能否接纳第四个月的进馆人次,并说明理由.
解:(1)设进馆人次的月平均增长率为x,由题意,得
128+128(1+x)+128(1+x)2=608.
化简,得4x2+12x-7=0.
解得x1=0.5=50%,x2=-3.5(舍去).
答:进馆人次的月平均增长率为50%.
(2)能.理由如下:
∵进馆人次的月平均增长率为50%,
∴第四个月的进馆人次为128(1+50%)3=128×=432<500.
答:学校图书馆能接纳第四个月的进馆人次.
17.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万千克与3.6万千克,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万千克.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
解:(1)设该养殖场蛋鸡产蛋量的月平均增长率为x,
根据题意,得2.5(1+x)2=3.6.
解得x=0.2,x=-2.2(不合题意舍去).
答:该养殖场蛋鸡产蛋量的月平均增长率为20%.
(2)设再增加y个销售点,
根据题意,得3.6+0.32y≥3.6×(1+20%),
解得y≥.
答:至少再增加3个销售点.
18.如图,在△ABC中,∠C=90°,AC=16
cm,BC=8
cm,一动点P从点C出发沿着CB边以2
cm/s的速度运动,另一动点Q从点A出发沿着AC边以4
cm/s的速度运动,P,Q两点同时出发,运动时间为t
s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
解:(1)根据题意,得S△PCQ=×2t(16-4t),S△ABC=×8×16=64.
∵△PCQ的面积是△ABC面积的,
∴×2t(16-4t)=64×.
整理,得t2-4t+4=0,解得t=2.
答:当t=2
s时,△PCQ的面积为△ABC面积的.
(2)△PCQ的面积不能与四边形ABPQ面积相等.理由如下:
当△PCQ的面积与四边形ABPQ面积相等时,则S△PCQ=S△ABC,即×2t(16-4t)=64×,
整理,得t2-4t+8=0.
∵Δ=(-4)2-4×1×8=-16<0,
∴此方程没有实数根.
∴△PCQ的面积不能与四边形ABPQ面积相等.
实际问题与一元二次方程
同步练习题
2021-2022学年人教版九年级数学上册第21章
一、选择题
1.秋冬季节为流感的高发期,有1人患了流感,经过两轮传染后共有81人患了流感.设每轮传染中平均一个人传染x个人,则所列方程正确的是(
)
A.x(x-1)=81
B.x(x+1)=81
C.(x-1)2=81
D.(1+x)2=81
2.某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程(
)
A.(x+1)2=43
B.x+2x+1=43
C.x2+x+1=43
D.x(x+1)=43
3.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元.若二月份到四月份每个月的月营业额增长率都相同,设增长率为x,根据题意可列方程(
)
A.82(1+x)2=82(1+x)+20
B.82(1+x)2=82(1+x)
C.82(1+x)2=82+20
D.82(1+x)=82+20
4.在一次九年级学生数学交流会上,每两名学生握手一次,统计共握手253次.若设参加此会的学生为x名,则可列方程为(
)
A.x(x+1)=253
B.x(x-1)=253
C.x(x+1)=253
D.x(x-1)=253
5.如图,把小圆形场地的半径增加5
m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为(
)
A.5
m
B.(5+)m
C.(5+3)m
D.(5+5)m
二、填空题
6.有1个人得流感病,第一轮传染6个人,第一轮过后共有7人得流感,第二轮传染时平均每人也传染6人,第二轮被传染了______人,第二轮过后共有______人得流感.
7.春节期间,某微信群规定,群内每个人都要发一个红包,并保证群内其他人都能抢到,且自己不能抢自己发的红包,此次抢红包活动中,群内所有人共收到90个红包.若设该群一共有x人,则可列方程为______.
8.如图,邻边不相等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18
m.若矩形的面积为36
m2,则AB的长度是______m.
9.两个数的积为12,和为7,设其中一个数为x,则依题意可列方程______.
10.如图,某单位准备在院内一块长30
m、宽20
m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的部分种植花草.要使种植花草的面积为532
m2,则小道进出口的宽度为______m.
三、解答题
11.如图,有一块矩形硬纸板,长30
cm,宽20
cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200
cm2?
12.某农场去年种植了10亩地的南瓜,亩产量为2
000
kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为______亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的,今年南瓜的总产量为60
000
kg,求南瓜亩产量的增长率.
13.如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,求这4个数中最小的数.
14.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·为政》
读诗词解题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
15.如图1,某小区的平面图是一个占地长500米,宽400米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形,如果要使四周的空地所占面积是小区面积的19%,南北空地等宽,东西空地等宽.
(1)求该小区四周的空地的宽度.
(2)如图2,该小区在东、西、南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东、西两侧绿化带完全相同,其长均为200米,南侧绿化带的长为300米,绿化总面积为12
500平方米,请算出小区道路的宽度.
16.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率.
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,学校图书馆能否接纳第四个月的进馆人次,并说明理由.
17.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万千克与3.6万千克,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万千克.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
18.如图,在△ABC中,∠C=90°,AC=16
cm,BC=8
cm,一动点P从点C出发沿着CB边以2
cm/s的速度运动,另一动点Q从点A出发沿着AC边以4
cm/s的速度运动,P,Q两点同时出发,运动时间为t
s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
参考答案
21.3
实际问题与一元二次方程
同步练习题
2021-2022学年人教版九年级数学上册第21章
一、选择题
1.秋冬季节为流感的高发期,有1人患了流感,经过两轮传染后共有81人患了流感.设每轮传染中平均一个人传染x个人,则所列方程正确的是(D)
A.x(x-1)=81
B.x(x+1)=81
C.(x-1)2=81
D.(1+x)2=81
2.某树主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支总数是43.若设主干长出x个支干,则可列方程(C)
A.(x+1)2=43
B.x+2x+1=43
C.x2+x+1=43
D.x(x+1)=43
3.某超市今年二月份的营业额为82万元,四月份的营业额比三月份的营业额多20万元.若二月份到四月份每个月的月营业额增长率都相同,设增长率为x,根据题意可列方程(A)
A.82(1+x)2=82(1+x)+20
B.82(1+x)2=82(1+x)
C.82(1+x)2=82+20
D.82(1+x)=82+20
4.在一次九年级学生数学交流会上,每两名学生握手一次,统计共握手253次.若设参加此会的学生为x名,则可列方程为(D)
A.x(x+1)=253
B.x(x-1)=253
C.x(x+1)=253
D.x(x-1)=253
5.如图,把小圆形场地的半径增加5
m得到大圆形场地,场地面积扩大了一倍,则小圆形场地的半径为(D)
A.5
m
B.(5+)m
C.(5+3)m
D.(5+5)m
二、填空题
6.有1个人得流感病,第一轮传染6个人,第一轮过后共有7人得流感,第二轮传染时平均每人也传染6人,第二轮被传染了42人,第二轮过后共有49人得流感.
7.春节期间,某微信群规定,群内每个人都要发一个红包,并保证群内其他人都能抢到,且自己不能抢自己发的红包,此次抢红包活动中,群内所有人共收到90个红包.若设该群一共有x人,则可列方程为x(x-1)=90.
8.如图,邻边不相等的矩形花园ABCD,它的一边AD利用已有的围墙(墙足够长),另外三边所围的栅栏的总长度是18
m.若矩形的面积为36
m2,则AB的长度是3m.
9.两个数的积为12,和为7,设其中一个数为x,则依题意可列方程x2-7x+12=0.
10.如图,某单位准备在院内一块长30
m、宽20
m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的部分种植花草.要使种植花草的面积为532
m2,则小道进出口的宽度为1m.
三、解答题
11.如图,有一块矩形硬纸板,长30
cm,宽20
cm.在其四角各剪去一个同样的正方形,然后将四周突出部分折起,可制成一个无盖长方体盒子.当剪去正方形的边长取何值时,所得长方体盒子的侧面积为200
cm2?
解:设剪去正方形的边长为x
cm,则做成无盖长方体盒子的底面长为(30-2x)cm,宽为(20-2x)cm,高为x
cm,
依题意,得2×[(30-2x)+(20-2x)]x=200.
解得x1=,x2=10.
当x=10时,20-2x=0,
故x=10不合题意,应舍去.
答:当剪去正方形的边长为
cm时,所得长方体盒子的侧面积为200
cm2.
12.某农场去年种植了10亩地的南瓜,亩产量为2
000
kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,设南瓜种植面积的增长率为x.
(1)则今年南瓜的种植面积为10(1+x)亩;(用含x的代数式表示)
(2)如果今年南瓜亩产量的增长率是种植面积的增长率的,今年南瓜的总产量为60
000
kg,求南瓜亩产量的增长率.
解:根据题意,得10(1+x)×2
000(1+)=60
000,
整理,得x2+3x-4=0,
解得x1=1=100%,x2=-4(不合题意,舍去).
∴x=50%.
答:南瓜亩产量的增长率为50%.
13.如图是一张月历表,在此月历表上可以用一个矩形任意圈出2×2个位置上相邻的数(如2,3,9,10).如果圈出的4个数中最大数与最小数的积为128,求这4个数中最小的数.
解:设这4个数中最小的数是x,则最大的数是x+8,根据题意,得
x(x+8)=128,
整理,得x2+8x-128=0.
解得x1=8,x2=-16(不合题意,舍去).
答:这4个数中最小的数是8.
14.子曰:“吾十有五而志于学,三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩.”——《论语·为政》
读诗词解题:
大江东去浪淘尽,千古风流数人物;
而立之年督东吴,早逝英年两位数;
十位恰小个位三,个位平方与寿符;
哪位学子算得快,多少年华属周瑜?
解:设周瑜逝世的年龄的个位数字为x,则十位数字为x-3,根据题意,得
10(x-3)+x=x2,
解得x1=5,x2=6.
当x=5时,周瑜的年龄是25岁,
∵而立之年为30岁,25<30,
∴x=5不符合题意,应舍去;
当x=6时,周瑜的年龄是36岁,符合题意.
答:周瑜的年龄是36岁.
15.如图1,某小区的平面图是一个占地长500米,宽400米的矩形,正中央的建筑区是与整个小区长宽比例相同的矩形,如果要使四周的空地所占面积是小区面积的19%,南北空地等宽,东西空地等宽.
(1)求该小区四周的空地的宽度.
(2)如图2,该小区在东、西、南三块空地上做如图所示的矩形绿化带,绿化带与建筑区之间为小区道路,小区道路宽度一致.已知东、西两侧绿化带完全相同,其长均为200米,南侧绿化带的长为300米,绿化总面积为12
500平方米,请算出小区道路的宽度.
解:(1)建筑区的面积是500×400×(1-19%)=162
000(平方米).
设建筑区的长度为5x米,则宽为4x米.根据题意,得5x·4x=162
000,整理,得x2=8
100.
解得x1=90,x2=-90(不合题意).
∴东西两侧道宽:(500-5x)÷2=25(米),
南北两侧道宽:(400-4x)÷2=20(米).
答:小区的东西两侧空地的宽度为25米,南北两侧空地的宽度为20米.
(2)设小区道路的宽度为z米,则
(20-z)×300+2×(25-z)×200=12
500.
解得z=5.
答:小区道路的宽度是5米.
16.习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩然之气.”某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率.
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,学校图书馆能否接纳第四个月的进馆人次,并说明理由.
解:(1)设进馆人次的月平均增长率为x,由题意,得
128+128(1+x)+128(1+x)2=608.
化简,得4x2+12x-7=0.
解得x1=0.5=50%,x2=-3.5(舍去).
答:进馆人次的月平均增长率为50%.
(2)能.理由如下:
∵进馆人次的月平均增长率为50%,
∴第四个月的进馆人次为128(1+50%)3=128×=432<500.
答:学校图书馆能接纳第四个月的进馆人次.
17.某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万千克与3.6万千克,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率.
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万千克.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
解:(1)设该养殖场蛋鸡产蛋量的月平均增长率为x,
根据题意,得2.5(1+x)2=3.6.
解得x=0.2,x=-2.2(不合题意舍去).
答:该养殖场蛋鸡产蛋量的月平均增长率为20%.
(2)设再增加y个销售点,
根据题意,得3.6+0.32y≥3.6×(1+20%),
解得y≥.
答:至少再增加3个销售点.
18.如图,在△ABC中,∠C=90°,AC=16
cm,BC=8
cm,一动点P从点C出发沿着CB边以2
cm/s的速度运动,另一动点Q从点A出发沿着AC边以4
cm/s的速度运动,P,Q两点同时出发,运动时间为t
s.
(1)若△PCQ的面积是△ABC面积的,求t的值.
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
解:(1)根据题意,得S△PCQ=×2t(16-4t),S△ABC=×8×16=64.
∵△PCQ的面积是△ABC面积的,
∴×2t(16-4t)=64×.
整理,得t2-4t+4=0,解得t=2.
答:当t=2
s时,△PCQ的面积为△ABC面积的.
(2)△PCQ的面积不能与四边形ABPQ面积相等.理由如下:
当△PCQ的面积与四边形ABPQ面积相等时,则S△PCQ=S△ABC,即×2t(16-4t)=64×,
整理,得t2-4t+8=0.
∵Δ=(-4)2-4×1×8=-16<0,
∴此方程没有实数根.
∴△PCQ的面积不能与四边形ABPQ面积相等.
同课章节目录
